Module 3
1. Module 3
1.4. Page 4
Module 3: Linear Measure
Bringing Ideas Together
In the Explore section you polished your estimation skills. Probably without even knowing it, you used an object or a part of your body to estimate lengths. In other words, you used a referent. For instance, you may have paced off the width of your front yard to estimate the distance in yards. Or you might have used your height to estimate the height of your bedroom. You may even have used the width of your thumb to estimate the length of your foot. You used referents in Unit 1 to explore SI and imperial units.
Self-Check
SC 1. What referents could you use for the units of measure in the following table? A common referent for the inch is given as an example.
|
Unit |
Referent |
|
1 in |
width of a thumb |
|
1 ft |
|
|
1 yd |
|
|
1 mm |
|
|
1 cm |
|
|
1 m |
|
SC 2. Use your referents from SC 1 to estimate the dimensions of the following common items. Give your answers in SI and imperial units.
- the height of your kitchen table
- the length, width, and height of your refrigerator
- the length, width, and height of your family’s or neighbour’s car or truck
- the length, width, and thickness of a magazine
Determining a Value for the Perimeter
Often you will need to find the perimeter or distance around an object in order to solve a problem. Knowing the perimeter is essential in tasks such as hanging wallpaper, fencing, installing baseboards, and framing pictures.
The applet, “Perimeter,” shows how to calculate the perimeter for a shape that is not regular. Select [PLAY] to watch the animation.
Example 1
© bhowe/shutterstock
Maxine is planning a rectangular patio for her backyard. She has room for a patio that measures 15 ft long × 12 ft wide. Maxine has decided that the patio will be built using interlocking bricks, but she wants a wooden frame around the perimeter. What is the total length of framing Maxine will need?
Solution
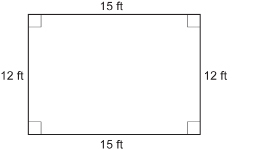
The perimeter, P, is the length of the four sides added together.
Maxine will need 54 ft of framing for her patio.
Formulas for Perimeter
You are probably familiar with the formulas for the perimeters of rectangles and squares.
If 
= length and w = width, the perimeter for a rectangle is
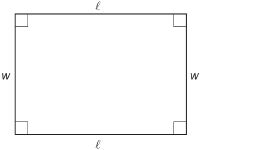
Open “Perimeter and Area (Rectangle).” This demonstration provides examples of perimeter calculations for rectangles. Move the - and w-slider to change the length and width of the rectangle. Make a rectangle the size of Maxine’s patio from Example 1. Did you get the same perimeter?
If s = length of each side, the perimeter for a square is
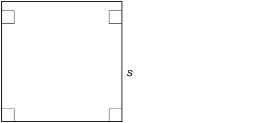
Open “Perimeter and Area (Square).” This demonstration provides examples of perimeter calculations for squares. Move the s-slider to change the side length of the square.
The following examples show how formulas can help you solve perimeter problems.
Example 2
Paula wants to purchase a decorative wallpaper border for her living room. The room is rectangular and measures 4 m by 5 m. How much border will Paula need to buy?
Solution
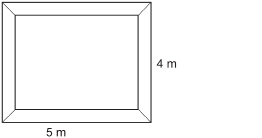
You are given w = 4 m and 
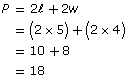
Paula will need to buy 18 m of wallpaper border.
How do you go the other way? How do you find the length of the sides when the perimeter is known? Work through Example 3 to find out.
Example 3
The perimeter of a square tile is 4 ft. How long is each side?
Watch “Example 3 Solution” to find out.
Perimeter of Irregular Shapes
If a shape is not rectangular or square, you will often need to work with the sides separately.
Example 4
A triangular flower bed is 12 ft × 5 ft × 14 ft. Luc wants to put a decorative border around the flower bed. What length of decorative border will he need?
Solution
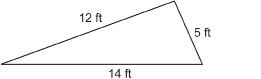
A total of 31 ft of decorative border is needed.
Self-Check
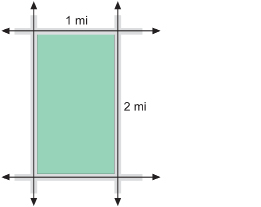
SC 3. In farming areas in Western Canada, north-south roads are normally two miles apart, and east-west roads are one mile apart. These roads divide the land into a plot.
How far would you drive to go around such a plot once?
SC 4. A road-maintenance worker is replacing the white reflective tape on the border of a stop sign. If the sign is 10 in on one side, how much tape will she need for the sign? Express your answer in feet and inches.
© Stacie Stauff Smith Photography/shutterstock
SC 5. The perimeter of a rectangular picture is 50 cm. If the width of the picture is 10 cm, what is the length of the picture?
Mastering Concepts
Try this question. When you are finished, check your answer.
A floor plan for a guest room is shown in the diagram. The guest room still needs baseboards installed. A student is helping his mother determine the length of baseboard needed.
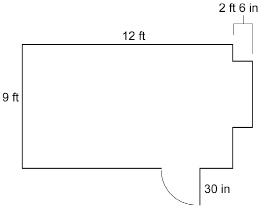
The student suggests finding the perimeter of the following figure to estimate the length of baseboard needed.
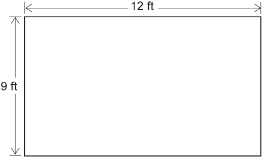
The student’s mother suggests the student needs to adjust her estimate to account for the 30-in doorway, because no baseboard will be needed for the doorway. Specifically, how does the doorway affect the length of baseboard needed? Her mother also comments that there’s a part of the wall that sticks out by 2 ft 6 in. How does that change things?
After their discussion, the student and her mother feel ready to purchase the right length of baseboard for the guest room.
Baseboard at the local building supply store sells for $0.86 per linear foot. How much would it cost to install baseboards in the guest room according to the floor plan?