Print this chapterPrint this chapter

Lesson 3

1. Lesson 3

1.2. Explore

Mathematics 30-3 Module 2

Module 2: Number

 

Explore

 

The strategies you used to solve the puzzles in Try This 1 may have been unique to you, or they may have been similar to your partner’s strategies. Here are some possible first steps for each of the puzzles in Try This 1.

1. Gears

2. Chickens and Pigs
This is a picture of five gears meshed together.

This is a picture showing 14 circles. Each circle has two line segments attached.

 

In each case, a picture was drawn as a starting point. This is a very common tool for solving problems of all types, including puzzles.

 

Self-Check 1
  1. Use the picture above to solve the Gears problem from Try This 1. Answer
  2. Use the picture above to solve the Chickens and Pigs problem from Try This 1. Answer
  3. Open Triangle of Coins and solve the puzzle. Answer

     
    This play button opens Triangle of Coins.
  4. Solve this Blocks of Wood puzzle.

     

    This is a picture of a 3 inch by 3 inch by 3 inch orange cube.
    iStockphoto/Thinkstock

     

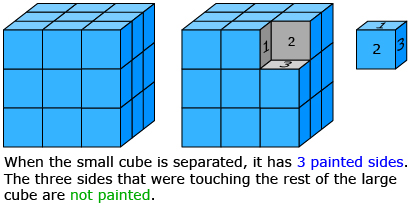
    Suppose you took a 3 inch × 3 inch × 3 inch cube made from joining 27 small cubes and dipped the cube in a can of paint. Each of these smaller cubes will have paint on 3, 2, 1, or 0 sides. How many cubes will have paint on 3, 2, 1, and 0 sides? Answer

  5. A famous logic puzzle is called Prisoners and Hats. There are many different versions available. Here is one version. Solve the puzzle.

     

    This is an illustration of three blue hats and two red hats.

    Three men are standing in a row, all facing the same direction. The man in the back can see the two men in front of him. The man in the middle can only see the man in front of him. The man in front cannot see either of the other two men.

    A hat is placed on the head of each man. There were three blue hats and two red hats to choose from, so two hats are left over.

    Each man cannot see the colour of the hat on his head, or the colours of the two leftover hats. They all know how many hats there were to start with, and they are told that any man who can determine the colour of the hat on his own head will win a prize.

    The man at the back said he didn’t know the colour of his hat. The man in the middle said he didn’t know the colour of his hat. The man in front said he knew the colour of his hat and he was correct.

    What colour was the hat of the man in front, and how did he know?

    You may want to draw pictures and try out different combinations.



    Answer
This diagram shows a cube made of 27 smaller cubes. The top right small cube has been removed in the second diagram to show that paint covers the three outer sides but not the three inner sides.
If the man at the back doesn’t know what colour his hat is, then there are only two possible combinations of hat colours for the front two men.
What would the man at the back conclude if he saw two red hats in front of him?