Print this chapterPrint this chapter

Lesson 4

1. Lesson 4

1.7. Explore 3

Mathematics 30-3 Module 5

Module 5: Geometry

 

A reflection is a mirror image created by transforming an original image over a line.

 

Source: MathWorks 12 Student Book/Teacher Guide. (Vancouver: Pacific Educational Press, 2011.)

Reflections are the next type of transformation you will examine.

 

Try This 3
  1.  
    1. Explain how symmetry could be used to complete the following picture.

       
      This diagram shows half of a girl’s face on a grid.
    2. Print Girl’s Face Diagram and complete the image using your strategy from question 1.a. One possibility for completing the picture is to use a reflection. To do this, pick key points, reflect them across the y-axis, and use the new points to guide where the rest of the drawing will go.

      Did You Know?

      This shows three versions of a picture of a face. One made with a left and right side, one made with a left side and a reflected left side, and one made with a right side and a reflected right side
      Thomas Northcut/Digital Vision/Thinkstock

      In reality most people’s faces are not symmetrical. Enter “facial symmetry” in your favorite search engine to see what many famous people would look like if their faces were symmetric. You can even take a picture of yourself and manipulate it to see what you would look like with a symmetric face.



  2. Use the key-point strategy to complete the following diagram using the steps provided.

     
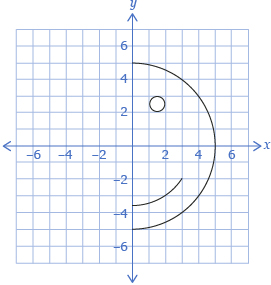
    This diagram shows half a happy face on a coordinate grid. The points A at (0, 5); B at (4, 3); C at (1.5, 2.5); D at (5, 0); E at (3, –1); F at( 0, –3); G at (4, –3); and H at (0, –5) are shown.
    1. Print Happy Face Diagram, which includes the key points.
    2. Determine the new location of each reflected point and draw the new points on the diagram. Label the new points with a prime symbol: ′. For example the point corresponding to A is A′.
    3. Complete the drawing.
    4. Determine the line of symmetry for this drawing.
  3.  
    1. Record all coordinates from the drawing in a table like the one shown.

      Original Point

      Reflected Point

      A(0, 5)

      A′(0, 5)

      B(4, 3)

      B′(−4, 3)

       

       

       

       

       

       

       

       
    2. Describe the relationship between the original points and the reflected points.
  4. Another common line of reflection, or axis of symmetry, is the x-axis.
    1. Predict how the original coordinates will change when a reflection occurs across the x-axis.

       
      This diagram shows a coordinate grid with the x-axis highlighted.
    2. Print Polygon Reflection Diagram, and reflect the polygon across the x-axis.

       
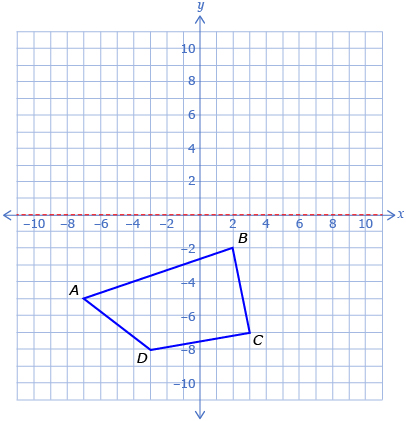
      This diagram shows a quadrilateral with points A at (–5, –5); B at (2, –2); C at (3, –7); and D at (–3, –8).
    3. Complete a table like the one shown.

      Original Point

      Reflected Point

      A(−7, −5)

      A′(−7, 5)

      B(2, −2)

       

      C(3, −7)

       

      D(−3, −8)

       
    4. Describe the relationship between the original points and the reflected points. How does this compare to your prediction?

course folder Save your responses in your course folder.

 

Share 2

 

With a partner or in a group, discuss the following questions.

  1. Compare the processes you used to reflect a shape.
  2. Describe the relationship between a line of reflection and a line of symmetry.

course folder If required, place a summary of your discussion in your course folder.

Each new point should be the same distance from the y-axis and directly horizontal from the original point.