Lesson 7

Lesson 7: Cosine Law

 

Focus

 

There are many instances where direct measurement is not possible. If you can create a triangle using values that can be measured, you can often use trigonometry to calculate the value that is needed.

 

Jennifer and David are designing an obstacle course. They have a number of different tasks that participants need to complete, and they need to determine their materials list to set up all of the tasks. They are able to measure angles and distances for many of the tasks. However, some of the tasks are not easily measurable.

 

For the first task, people will need to hang on to a rope while crossing a rapidly flowing river that is about 1 m deep. Jennifer and David need to know the distance across the river to be sure that the rope is long enough. They don’t have a tape measure long enough to measure the river's width, so they decide to create a triangle using measurements that they can make in order to calculate this value.

 

David and Jennifer know the measures of the canyon walls and the angle at the bottom of the canyon, as shown in the following diagram. The rope corresponds to side c.

 

 

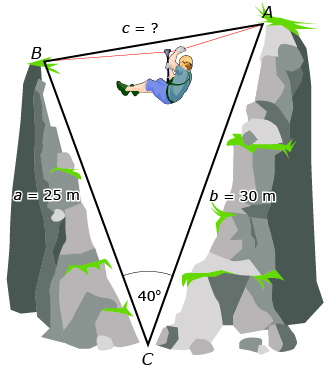
As you work through this lesson you will discover how David and Jennifer can determine the value of c and find the amount of rope they will need.

 

Lesson Outcomes

 

At the end of this lesson you will be able to

• determine an unknown length in a triangle using the cosine law
• determine an unknown angle in a triangle using the cosine law

Lesson Question

 

You will investigate the following question:

• How can the cosine law be used to solve problems?

Assessment

 

Your assessment may be based on a combination of the following tasks:

• completion of the Lesson 7 Assignment (Download the Lesson 7 Assignment and save it in your course folder now.)
• course folder submissions from Try This and Share activities
• additions to Glossary Terms
• work under Project Connection

Materials and Equipment

• calculator