Print this chapterPrint this chapter

Lesson 7

1. Lesson 7

1.5. Explore

Mathematics 30-3 Module 5

Module 5: Geometry

 

Explore

 

In Discover, you were introduced to the cosine law in the form a2 = b2 + c2 − 2bc cos A. Like the sine law, the cosine law can be used with any triangle. The cosine law can be used if the length of the three sides are known (SSS) or the length of two sides and the enclosed angle are known (SAS).

 

The cosine law can be used on Jennifer and David’s scenario, since SAS applies. A possible solution to their problem follows.

 

Write out the equation. a2 = b2 + c2 − 2bc cos A
Substitute the known values. a2 = 302 + 252 − 2(30)(25) cos 40°
Simplify each term. a2 = 900 + 625 − 1149.1
Simplify the expression. a2 = 375.9
Take the square root of both sides of the equation. a = 19.4


Therefore, Jennifer and David will need a rope long enough to cross a 19.4-m gap.

 

 

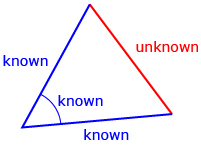
This diagram shows a triangle. One angle is labelled “known” and the two sides meeting that angle are also labelled “known.” The side across from the known angle is labelled “unknown.”

 

To label a triangle, use the same strategy used with the sine law, with angles given a capital letter and sides given a lowercase letter. Remember that an angle and the side across from the angle will get the same letter.

 

To use the equation a2 = b2 + c2 − 2bc cos A, always label the unknown side a and the angle across from the unknown side A. It does not matter which side you give the labels b and c to after a and A are labelled.

 

 

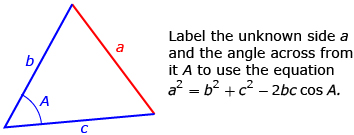
This diagram shows a triangle. One angle is labelled A and the two sides meeting that angle are labelled b and c. The side across from the known angle is labelled a.

 

Watch Cosine Law Illustrator. This presentation reviews the relationship between the cosine law and the parts of a triangle.

 

 

This is a play button that opens Cosine Law Illustrator.

 

Self-Check 1

 

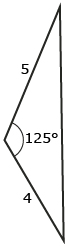
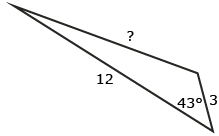
Label each triangle so you can use the cosine law, a2 = b2 + c2 − 2bc cos A, to determine the unknown side. (You don’t need to determine the unknown side.)


  1. This shows a triangle with an angle of 125 degrees. The side across from the 125-degree angle is labelled with a question mark, and the sides beside the 125-degree angle are labelled “4” and “5.”

    Answer

  2. This shows a triangle with an angle of 43 degrees. The side across from the 43-degree angle is labelled with a question mark, and the sides beside the 43-degree angle are labelled “3” and “12.”

    Answer

Once a triangle has been labelled properly, the cosine law (a2 = b2 + c2 − 2bc cos A) can be used to determine the length of the unknown side a. Read “Example 1” on page 261 of the textbook to see another example of how the cosine law can be used to determine the length of an unknown side. Pay attention to how the triangle was labelled before the cosine law was used.

 

Self-Check 2


textbook
Answer “Build Your Skills” questions 1, 2, 3, and 5 from pages 266 to 268. Answer