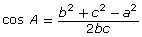Lesson 7
1. Lesson 7
1.6. Explore 2
Module 5: Geometry
Thus far you have used the cosine law to determine the length of an unknown side of a triangle. It is also possible to use the cosine law to determine the value of an unknown angle. Try This 2 explores this idea.
Try This 2

iStockphoto/Thinkstock
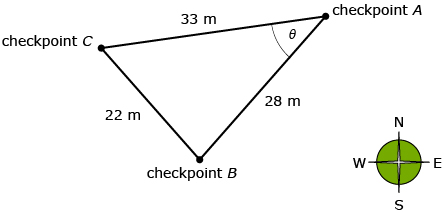
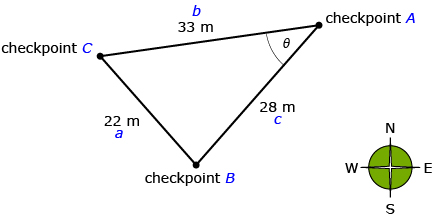
Sandra is taking the same orienteering course as Jeremy in Lesson 6. Sandra is standing at Checkpoint A and knows the distances between all the checkpoints, as shown in the diagram. In order to walk in the correct direction, she needs to determine the angle between Checkpoint B and Checkpoint C, represented by θ on the diagram.
-
- Sketch the diagram. Label the sides and angles appropriately.
- Use a “guess and check” strategy with the equation a2 = b2 + c2 − 2bc cos A to determine the value of θ in the diagram.
-
- Using a “guess and check” strategy can take a long time. A better strategy may be to solve the formula for A. Try isolating A in the equation a2 = b2 + c2 − 2bc cos A using the following steps. Make sure to write each step on a new line.
- Subtract b2 and c2 from both sides of the equation.
- Divide both sides of the equation by −2bc.
- Apply the inverse cosine (cos−1) to both sides of the equation.

- Use the equation you determined in part a. to determine the value of θ in the diagram. How did this value compare to the one you determined in question 1. b?

- Using a “guess and check” strategy can take a long time. A better strategy may be to solve the formula for A. Try isolating A in the equation a2 = b2 + c2 − 2bc cos A using the following steps. Make sure to write each step on a new line.
![]() Save your responses in your course folder.
Save your responses in your course folder.
If you know all three sides of a triangle, you can use the cosine law to determine an unknown angle. It is possible to rearrange the equation a2 = b2 + c2 − 2bc cos A to allow you to determine unknown angles more easily.
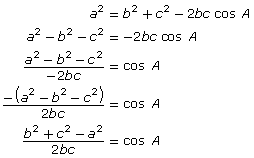
The equation ![]() can be used to determine cos A. To determine the degree measurement of A, find the inverse cosine (cos−1) of both sides of the equation.
can be used to determine cos A. To determine the degree measurement of A, find the inverse cosine (cos−1) of both sides of the equation.
This equation can be used to determine the unknown angle in Try This 2 as follows.
| Write out the equation. | ||
| Substitute the known values. | ||
| cos A = 0.7516… |
|
When entering fractions on a calculator, extra care must be taken with brackets. The easiest approach is to always put the numerator in brackets and the denominator in brackets.
For this example, you would enter the following in your calculator: |
| A = cos−1 (0.7516…) | Use the inverse cosine (cos−1) to determine A. | |
| A = 41.268…° | The rounded value of A is 41.268…°. | |
| A = 41° | Round to the nearest degree, unless instructed otherwise. | |
Read “Example 2” on pages 262 and 263 of the textbook to see how all three angles of a triangle can be determined if you know all three sides.
Self-Check 3
Add the following formulas to your copy of Formula Sheet:
- a2 = b2 + c2 − 2bc cos A