Lesson 6: Surface Area and Volume Problem Solving
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 6: Surface Area and Volume Problem Solving |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 3:27 AM |
Focus

© Jose Marines/shutterstock
How would you describe your favourite place to someone who has never been there? That place might be your bedroom at home, a cabin at the lake, or an ancient castle from your imagination. You could definitely use photos and drawings; but you also need a way to describe the size or dimensions of your place.
As you have been working on your math and spending time around your home and school, maybe you have noticed some basic geometric shapes in your environment. A single structure or space, such as the pictured castle, often includes a variety of geometrical shapes—prisms, pyramids, cones, cylinders, and spheres, for example.
If you have a structure that is made of more than one shape, how could you calculate its surface area and volume? What strategies can you develop to investigate the surface area and volume of complex shapes?
Outcomes
At the end of this lesson, you will be able to do the following:
- Solve problems that involve surface area and the volume of 3-D objects.
- Determine an unknown dimension of a right cone, cylinder, prism, pyramid, or sphere, given the object’s surface area or volume and the remaining dimensions.
- Solve problems that involve surface area or volume, given a diagram of the composite 3-D object.
- Describe the relationship between the volumes of right cones and cylinders with the same height and base and right pyramids and prisms with the same height and base.
Lesson Questions
- Why is visualization important to the study of the surface area and volume of 3-D objects?
- How does changing the dimensions of an object affect its surface area and volume?
![]() Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Assess tab or by using the Quizzes link under the Activities block.
** Note – Share questions may have to be done on your own depending on your learning situation**
Launch
Are You Ready?
Complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
1. In your own words, define the following:
a. surface area
b. volume
2. a. For each of the following 3-D shapes, determine the surface area.

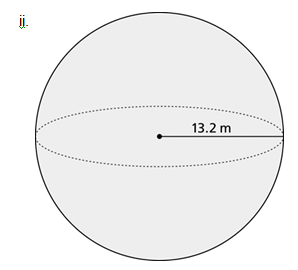
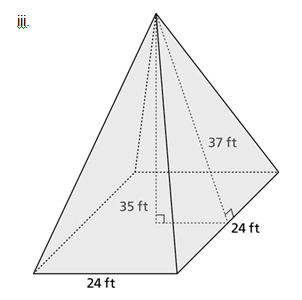
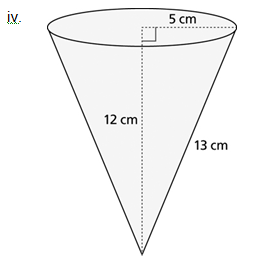
b. Determine the volume for each of the 3-D shapes in part a.
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
![]() Refresher
Refresher
The interactive applet titled “Exploring Surface Area, Volume, and Nets—Use It” can help you review many aspects of surface area and volume. You will find the interactive piece on the right-hand side of the website.
Select the “Use It” tab at the bottom of the activity to review the nets of all of the 3-D objects that were previously explored. The activity tests your ability to visualize the net of a given 3-D object.
Select the “Explore It” tab to review the surface area and volume formulas for all of the 3-D objects previously introduced. This applet also enables you to do a side-by-side comparison of two formulas. For example, you can use this feature to compare
- the surface area formula of a sphere and the volume formula for a sphere
- the volume formulas of a cylinder and a cone
You can also access a video that demonstrates how math is used in designing large inflatable shapes. On the left-hand side of the website, choose “Exploring Surface Area and Volume (Video Interactive)” to view the video.
Discover
How does adjusting the dimensions of a 3-D object affect its surface area and volume? In the following Math Lab, you will investigate this question.
![]() Math Lab: Surface Area and Volume Analysis
Math Lab: Surface Area and Volume Analysis
Go to Math Lab: Surface Area and Volume Analysis, print it (or copy by hand) and complete it. Save your work in your course folder (binder).
![]() Share
Share
Take a look at the results from Math Lab: Surface Area and Volume Analysis.
It seems reasonable to assume that as the dimensions of an object are doubled, the surface area and volume are also doubled. Yet the results of the investigation proved otherwise.
In fact, you may have found that as the dimensions are doubled, the surface area is quadrupled, or increases by a factor of four.
At the same time, the volume undergoes an increase by a factor of eight! Where do these numbers come from?
Review your lab results and see if you can see any patterns in the ratios.
You may want to extend the investigation by quadrupling each dimension; then recalculate the surface area or volume.
Develop an explanation for how to predict the increase in surface area or volume.
Use your explanation to predict how the surface area and volume will change when the dimensions of an object are increased by a factor of 7.
If possible, work with other students to see if you can develop a formula or pattern for the change in surface area and volume.
To check your work, use the link below.
Explore

© Jim Parkin/shutterstock
As you look around your surroundings, you may find objects that resemble the 3-D objects studied in the previous two lessons. A soup can, a box, and a ball are examples of cylinders, prisms, and spheres, respectively. A pylon used to alert motorists of traffic obstructions resembles a cone, and some games use pyramid-shaped dice.
While there are many examples of prisms, pyramids, cylinders, spheres, and cones, you may notice that many other objects are actually composites of two or more of these basic 3-D objects.
The image of the industrial propane tank is an example of a composite figure. Can you tell what 3-D objects are used in the tank’s design?
Glossary Terms
Throughout Module 1, you have been adding and saving math terms to “Glossary Terms” in your binder.
In this lesson the suggested terms for your glossary are
- composite figure
- hemispherical
- surface area to volume ratio
Return your updated “Glossary Terms” to your course folder (binder).
----------------------------------------
![]() Tip
Tip
In complex problems that have more than one three-dimensional shape, it is a good strategy to break the problem into parts so you are dealing with only one shape at a time.
In the case of the propane storage tank shown in the photo, you may want to determine its volume by first determining the volume of the cylinder and then determining the volume of the hemispheres (or half-spheres) on each end.
--------------------------------------
The steps below will help you to solve a surface area or volume problem:
Step 1: Decide which 3-D object or objects can be used to model the problem.
Step 2: Draw a rough sketch of this 3-D object, and label its dimensions.
Step 3: Decide which formulas you will use. You may need to select more than one formula in the case of composite figures. You might also find that you will need to modify the formula to fit the problem.
Step 4: Substitute given values into your formulas to solve the problem.
![]() Read
Read
Work through the following textbook examples that show how problems involving composite figures are solved. In the solutions, pay attention to
- the importance of an accurate drawing
- any preliminary calculations that need to be made
- the sequence of steps
Read “Example 1: Determining the Volume of a Composite Object” on pages 56 and 57 in your textbook. Then read “Example 2: Determining the Surface Area of a Composite Object” on page 57. Finally, read “Example 3: Solving a Problem Related to a Composite Object” on page 58.
![]() Self-Check
Self-Check

© Sue Smith/shutterstock
SC 1. A grain storage bin has a diameter of 4.8 m. The height of the straight side wall is 10 m. The cone top has an additional height of 1.5 m.
- What is the total volume of this bin?
- Suppose you want to paint the outside of one of the grain storage bins. If the slant height of the conical roof is 2.83 m, then what total surface area needs to be painted?

SC 2. Mr. Vanilla charges 0.5 cents/cm3 for his ice cream. How much would you pay for one spherical-shaped scoop of ice cream if a scoop of ice cream has a radius of 3.5 cm?
- $8.99
- $1.50
- 26 cents
- 90 cents
SC 3. The right cylinder and right cone shown have the same radius and volume. The cylinder has a height of 12 in. What is h, the height of the cone?

- 18 in
- 24 in
- 36 in
- 42 in
SC 4. A glass containing water is in the shape of a right circular cylinder with a radius of 3 cm. The height of the water in the glass is 10 cm.
- What is the volume of the water in the glass? Be sure to include units of measure in your answer. Show or explain how you obtained your answer.
- Five spherical marbles of equal size are dropped into the glass. The water in the glass rises to a height of 11 cm. What is the increase in the volume of the glass contents? Be sure to include units of measure in your answer. Show or explain how you obtained your answer.
- What is the volume of one marble? Be sure to include units of measure in your answer. Show or explain how you obtained your answer.
- What is the radius of one marble? Be sure to include units of measure in your answer. Show or explain how you obtained your answer.
![]() Try This
Try This
How did you do on the Self-Check questions?Complete TT1 for more practice:
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 1. Complete “Exercises” questions 3, and 9 on pages 59 and 60.
Use the link below to check your answers to Try This 1.
----------------------------------------
![]() Caution
Caution
There are a few myths about surface area and volume you may hear. These are all INCORRECT.
- Surface area can be found only for two-dimensional objects.
- Surface area is a concept used only in mathematics classes.
- You cannot measure the volume of some objects because they do not have “regular” lengths, widths, or heights.
- An object’s volume is greater in water than in air.
Connect
![]() Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Assess tab or using the Quizzes link under the Activities block. Also ensure your work in your binder (course folder) is complete.
![]() Project Connection: The Woodshed **NOT ASSIGNED**
Project Connection: The Woodshed **NOT ASSIGNED**
Up to this point in the project, you have all been working with your own place. For this lesson, you will do a common problem. You will consider the dimensions of a woodshed.
Of course, it is still a collaborative approach—you can still work together with a partner.
Go to the Unit 1 Project and complete the Lesson 6 portion of the project.
![]() Going Beyond
Going Beyond
The ratio between an organism’s surface area and volume has an enormous impact on its biology. For example, a cell that is shaped like a sphere has a low surface area to volume (SA : V) ratio.

© Nancy Nehring/iStockphoto

iStockphoto/Thinkstock
Cells that are extended (e.g., cylinder) have much more membrane per unit of cytoplasm, which means these cells have more surface area for each bit of goo inside of them. Extending the outer surface of a cell into fingers, like an amoeba, or indentations, like the red blood cells shown above, can greatly increase the total surface area.
Interestingly, scientists are identifying the ratio between the surface area and volume as a crucial factor in work with nanotechnology. Take a look at the nanobot in the second visual of red blood cells. What do you suppose its function is?
To find out more, perform an Internet search using the following keywords: “nanotechnology,” “surface area,” “volume,” “nanobot,” and “red blood cells.”
Summary
- Why is visualization important to the study of the surface area and volume of 3-D objects?
- How does changing the dimensions of an object affect its surface area and volume?
In this lesson you solved problems involving the surface area and volume of 3-D objects. You learned how to approach problems involving composite figures. You learned that it is important to visualize each problem before putting pencil to paper.
You also learned that doubling the dimensions of a 3-D object, such as a prism or a cone, actually increases its surface area by a factor of 4 and its volume by a factor of 8.
You also looked at common myths regarding surface area and volume. Through research, you were able to find explanations that dispelled these myths.
You are now ready to proceed to Assignment 1 and complete it.
