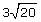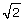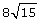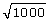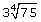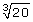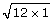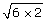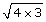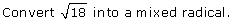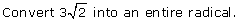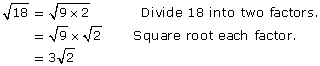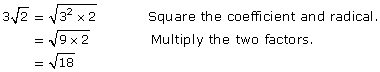Lesson 4: Mixed and Entire Radicals
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 4: Mixed and Entire Radicals |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 4:09 AM |
Module 2: Roots and Powers
Lesson 4: Mixed and Entire Radicals
Focus

© yuyangc/shutterstock
In this lesson you will learn how to simplify radicals. You use radicals when you apply the Pythagorean theorem. In Module 1 you solved surface area and volume problems that involved the use of radicals. Solving other equations in mathematics may also involve radicals.
Like the irrational numbers you learned about in Lesson 3, radicals can be used in the creation of secret codes. In fact, a cipher has been developed to improve the security of e-mails. A computer scientist named Michael Rabin developed a system that uses the squaring of numbers to convert plaintext to ciphertext to keep the contents secret. For decryption, he uses radicals!
Outcomes
At the end of this lesson, you will be able to demonstrate an understanding of radicals by
- expressing a radical as a mixed radical in simplest form
- expressing a mixed radical as an entire radical
- explaining, using examples, the meaning of the index of a radical
- ordering a set of radicals on a number line
Lesson Questions
- How are mathematical processes reversed?
- How can the properties of radicals be used to simplify and order irrational numbers?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Assess tab or by using the Quizzes link under the Activities block.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 2: Roots and Powers
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
1. List all the prime numbers between 1 and 20.
2. What is the prime factorization of 180?
3. Use prime factorization to determine the square root of 324.
4. Use prime factorization to determine the cube root of 1000.
5. Complete the table by listing the squares of each natural number from 1 to 15. The first three perfect squares have been done as an example.
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
You may find the following useful for reviewing these skills.
In Lesson 1 you created a chart of all the prime numbers between 1 and 100. Retrieve this chart and review the prime numbers in the first two rows.
The “Prime Factorization” applet demonstrates how you can use a factor tree to express a number as a product of primes. Use the applet to get the prime factorization of numbers such as 324 and 1000.
 Read
Read
Go to the textbook and work through the following examples to see how prime factorization is used to identify numbers as perfect squares or perfect cubes. This method also helps you determine the square roots and cube roots of those numbers. As you read, focus on how the prime factors are regrouped into identical groups to find the square and cube roots.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Determining the Square Root of a Whole Number” on page 144 and “Example 2: Determining the Cube Root of a Whole Number” on page 145.
Go to “Exploring Square Roots” to explore perfect squares and non-perfect squares. If you are not sure what the difference is, then you should really check this out. You can get the most out of this applet by answering the questions that are posed. The feedback will help you gain a better understanding of the concepts presented.
Module 2: Roots and Powers
Discover
In this lesson you will learn how to convert radicals from one form to the other. In order to do so, you need to know how to manipulate radicals. This activity will help you to become more comfortable working with radicals.
 Try This 1 - 2
Try This 1 - 2
Print out (or copy by hand) and complete the following Try This 1 and 2 activities in your course folder ( binder).
TT1 and 2 Activities
Once you complete these activities, check your work using the link below.
Module 2: Roots and Powers
Explore

© moxduul/shutterstock
The word radical has both Latin and Greek origins. From Latin, it means “root” and in Greek it means “branch.” In Lesson 2 you discovered ways to calculate the square root of a perfect square and the cube root of a perfect cube. In this lesson you will learn how to work with the roots of numbers that are not perfect squares or perfect cubes.
Glossary Terms
Add the following suggested glossary terms:
- entire radical
- index
- mixed radical
- radical
- radicand
- root
--------------------------------------------------------
Recall your work with the volumes of cubes. If you know the volume of a cube is 27 cm3, then you can determine the length of one side by using the formula V = s3. Here, V is the volume of the cube and s is its side length.
V = s3
27 = s3
To obtain the answer, you would cube root both sides of the equation. (Again, you may want to use your Perfect Squares and Perfect Cubes Data Sheet you created in Lesson 2 and saved in your course folder.)
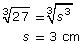
In this example you determined the cube root of 27 to find the side length of the cube. The expression 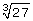 is called a radical.
is called a radical.
Study the diagram to understand how to name the parts of a radical.
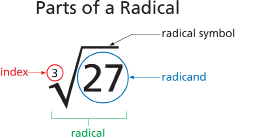
The radicand is the number or expression that appears underneath the radical symbol.
The index identifies the type of root. For example, a square root has an index of 2. A cube root has an index of 3. A fourth root has an index of 4, and so on.
 Tips
Tips
In the case of square roots where the index is not shown, the index is assumed to be 2.
For example, the index for each of the following radicals is 2:

Sometimes a radical may have a coefficient, or a number in front of the radical symbol, separated from the radicand. A radical whose coefficient is a number other than 1 is called a mixed radical. On the other hand, a radical with a coefficient equal to 1 is called an entire radical. The following chart has examples of mixed radicals and entire radicals.
|
Mixed Radicals |
Entire Radicals |
|
|
|
|
|
|
|
|
|
 Caution
Caution
There is a difference between  and
and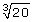 .
.
The radical  means three times the square root of 20 and is approximately equal to 13.4164.
means three times the square root of 20 and is approximately equal to 13.4164.
The radical 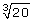 means cube root of 20 and is approximately equal to 2.7144.
means cube root of 20 and is approximately equal to 2.7144.
In Lesson 2 you learned how to find the square and cube roots of perfect squares and perfect cubes.
What if you are asked to find the square root of a non-perfect square such as 12? Well, you might say that ![]() is an irrational number. You could find a decimal approximation, but the only way to get an exact value is by simplifying the radical.
is an irrational number. You could find a decimal approximation, but the only way to get an exact value is by simplifying the radical.
In the Discover section you found out the square root of the product of two numbers is equal to the product of the square roots of those numbers. This property can be summarized with the following expression:
![]() where a and b are positive numbers
where a and b are positive numbers
For instance, the expression ![]() can be evaluated as
can be evaluated as![]() .
.
The following example uses this concept to simplify![]() .
.
Example 1
Simplify ![]() .
.
Solution
The radical ![]() could be expressed as the product of square roots in several ways:
could be expressed as the product of square roots in several ways:
|
|
This is not helpful as it is exactly the same as the original radical, |
|
|
This expression simplifies to |
|
|
This expression is the most helpful one because it simplifies to |
Sometimes, a radical is not a perfect square, but it may have a perfect square amongst its factors. To simplify the radical, you need to rewrite the radicand as a product of two factors, one of which is a perfect square. You can then simplify the square root of the perfect square and reduce the radicand. This process may need to be repeated until the radicand can no longer be reduced.
Example 2
Simplify the radical ![]()
Solution
Method 1: Perfect Square Factors

or look for the largest perfect square and get
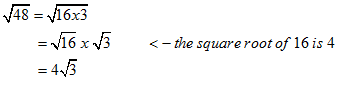
Method 2: Prime Factorization
 Watch and Listen
Watch and Listen
Watch “Simplifying Radicals” that demonstrates the method by prime factorization.
Did you notice the result of simplifying an entire radical, ![]() is a mixed radical,
is a mixed radical, ![]()
 Share
Share
Compare your answers to the following questions with another classmate or appropriate partner ( if possible).
1. In Method 1, how can you avoid repeated factoring of the radicand?
2. In Method 2, how do pairs of identical factors become simplified? Can you show the math that makes this possible?
Record any similarities and differences you discussed in your course folder (binder).
Example 3
You can apply the same techniques to simplify radicals of different indices (plural form of index).![]()
Solution
Method 1: Perfect Cube Factors
Method 2: Prime Factorization
Module 2: Roots and Powers
 Read
Read
Go to the textbook and work through the examples to further see how this is done. Pay attention to how the method is different from simplifying square roots.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Simplifying Radicals Using Prime Factorization” on page 215 and “Example 2.b): Writing Radicals in Simplest Form” on page 216.
Example 1.a) is a reminder of how to use prime factors to simplify a radical with index 2. Example 1.b) and 1.c) show a similar method for simplifying radicals with index 3 and index 4. Example 2.b) demonstrates what happens in the case of a number with no perfect square factors.
You have learned to simplify entire radicals by converting them into reduced mixed radicals. There will be some cases, however, where it is helpful to do the opposite. Read the next example to see how you can convert mixed radicals into entire radicals.
Example 4
Write 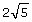 as an entire radical.
as an entire radical.
Solution
What distinguishes an entire radical from a mixed radical is that the entire radical does not have a coefficient. So, the objective is to determine the value of the radicand.
Method 1: Perfect Square Factors
The number 2 can be written as 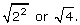
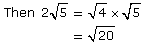
Method 2: Prime Factorization
Remember that the coefficient of 2 came from a pair of 2s under the radical symbol.
Write 2 as 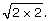
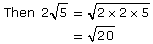
Example 5
Write 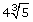 as an entire radical.
as an entire radical.
Solution
Using the method of prime factorization, write 4 as 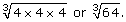
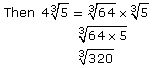
 Read
Read
At this point, if you think you understand how to convert from entire radicals to mixed radicals and vice versa, proceed to the Self-Check. Otherwise go to the textbook and work through the next example for more help with this concept.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 3: Writing Mixed Radicals as Entire Radicals” on page 217.
How does the index help you to convert to an entire radical?
In the previous lesson you learned how to locate irrational numbers on a number line. In this lesson you have learned to convert mixed radicals to entire radicals. Both these concepts can be applied to the ordering of irrational numbers on a number line. Study the following example to see how each method is applied.
Example 6
Order these irrational numbers from least to greatest: 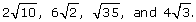
Solution
Method 1: Number Line
Enter the radicals into your calculator to obtain a decimal approximation of each one.
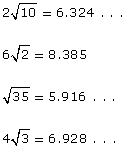
Putting these on a number line will give you the correct order:
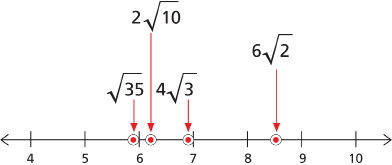
Method 2: Conversion to Entire Radicals
Convert each of the mixed radicals into entire radicals: 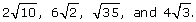
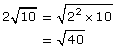
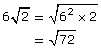
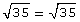
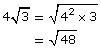
Since each of the radicals has the same index, you only need to compare the radicands.
The correct order from least to greatest is
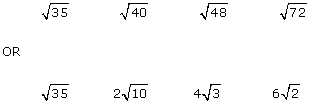
 Self-Check
Self-Check
SC 1. Simplify 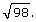
SC 2. Rewrite 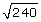 as a mixed radical.
as a mixed radical.
SC 3. Express 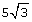 as an entire radical.
as an entire radical.
SC 4. Convert 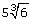 to an entire radical.
to an entire radical.
 Try This 3
Try This 3
Put your knowledge to the test by working through some of the questions from your textbook. When you are converting a mixed radical to an entire radical, pay attention to the index so you know how many factors of the coefficient you need to multiply with the radicand. When you are converting an entire radical, take an extra moment to make sure you have expressed the radicand as a product using the largest possible perfect square as a factor. This will help you avoid repeated multiplication.
Complete the following in your course folder ( binder).
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 3. Complete “Exercises” questions 4, 5, 11.a), 11.b), 11.c), 11.d), 12.a), 12.b), 12.c), and 12.d) on page 218.
Use the link below to check your answers to Try This 3.
Possible TT3 (Try This 3) Solutions
 Tips
Tips
It is really important to take a close look at the index before you work with a radical. If the index is not there, it is understood to be 2 (or the square root) and you are looking for one of two equal factors. If the index is 3 (the cube root), you are looking for one of three equal factors, and so on.
Module 2: Roots and Powers
 Lesson Assessment
Lesson AssessmentComplete the lesson quiz posted under the Assess tab or by using the Quizzes link under the Activities block. Also, ensure your work in your binder (course folder) is complete.
 Project Connection ** NOT ASSIGNED**
Project Connection ** NOT ASSIGNED**
There is no project component in this lesson. You will continue working on your project in the final two lessons of this module.
 Going Beyond
Going Beyond
Before the advent of calculators, the evaluation of square roots was performed using paper-and-pencil methods.
Step 1: Start an Internet search and use the keywords “Newton’s method square root” or “Babylonian method” to discover the steps for finding square roots without a calculator.
Step 2: Choose one of these methods and write down the steps.
Step 3: Apply the method to the following questions:
- Evaluate
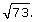
- Evaluate
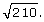
Module 2: Roots and Powers
Lesson 4 Summary

© fred goldstein/shutterstock
No one ever wants to be involved in a collision! Suppose you know the distance you need to stop your car, but can you stop it at the speed you are travelling? A very important application of radicals helps you find the maximum speed of a car to stop in a certain distance. The experimentation with objects in motion has shown that a relationship exists among the variables. For example, when you double your speed, your stopping distance quadruples.
Physicists have worked to create a formula that shows speed and stopping distance
|
|
The variable S is the maximum speed. |
|
The variable a is the braking deceleration. |
|
|
The variable d is the distance. |
In this radical expression, clear evidence is shown for why drivers should slow down in urban areas; a small reduction in speed leads to a much larger reduction in stopping distance. Solving the radical equation correctly here could quite literally save your, or someone else’s, life!
In Lesson 4 you investigated the following questions:
- How are mathematical processes reversed?
- How can the properties of radicals be used to simplify and order irrational numbers?
In this lesson you learned to identify the parts of a radical. You learned that an index of 2 means you can take one of two equal factors out from under the radical symbol. In a similar way, an index of 3 means you can take one of three equal factors out from under the radical symbol. By converting mixed radicals of the same index into entire radicals, you learned that you can compare the radicands to determine the correct sequence when ordering irrational numbers.
When you are encrypting a message, it is critical for you to be able to decrypt the code at a later time. Decryption is the reverse process of encryption. In a previous lesson you learned that you can reverse the single-step mathematical process of squaring by square rooting. Similarly, you can reverse the cubing of a number by evaluating the result’s cube root. In this lesson you examined another kind of mathematical process and its reverse process—converting between mixed radicals and entire radicals. Converting from an entire radical to a mixed radical is a two-step process. In the case of radicals with an index of 2, you first have to express the radicand as a product of two factors—a perfect square and a non-perfect square—and then you square root each factor. To reverse this you have to not only reverse each step but also in the reverse order.
Compare the following:
|
|
|
|
|
|
Notice that to convert to a mixed radical, you need to divide and then square root. On the other hand, to convert back to an entire radical, you need to square and then multiply. Therefore, each step is reversed, and the order of these steps is also reversed. The reversibility of processes is a recurring concept in mathematics. You will see this again in future courses when you examine inverse relations.
In the next lesson you will review the exponent laws. You will see by the last lesson of this module how radicals and exponents are related to each other. You will also learn how to convert between radicals and powers with rational exponents.