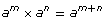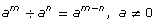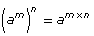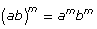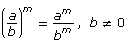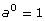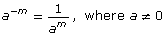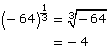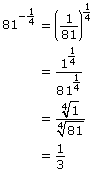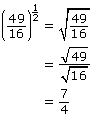Lesson 6: Rational Exponents
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 6: Rational Exponents |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 4:09 AM |
Module 2: Roots and Powers
Lesson 6: Rational Exponents
Focus

© Andresr/shutterstock; © Horst Petzoid/shutterstock
There is currently exponential growth in smartphones and social networking and, for some people, this is a cause for concern. When important information is on a work computer, there is not much chance it could be lost or stolen, but with smartphones that is changing.
Encryption has been used for years to keep important information secure. Most computer databases support encryption of sensitive tables, rows, or columns. That means everything in the database is secure, but it slows down access to the information.
A new direction some companies are taking is to decide what must be secure. If there are only a few sensitive columns (such as a customer’s credit card number, bank account number, or social insurance number), then only those columns need to be encrypted. This allows easier and faster information sharing while still protecting sensitive information. As the world changes, encryption changes too.
Outcomes
At the end of this lesson, you will be able to
- express powers with rational exponents as radicals and vice versa
- solve a problem that involves exponent laws or radicals
- identify and correct errors in a simplification of an expression that involves powers
Lesson Questions
- How are powers and radicals related to each other?
- How do you determine and understand error in mathematics?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Assess tab or by using the Quizzes link under the Activities block.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 2: Roots and Powers
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are you Ready?
Complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
1. a.Outline the steps used to add/subtract fractions.
b. Outline the steps used to multiply fractions.
2. Evaluate the expressions without a calculator. Simplify where possible.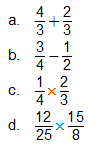
3. What is the formula relating a sphere’s volume and radius?
4. Find the radius of a sphere, to the nearest mm, if its volume is 905 mm3.
5. Name the parts of a power and the parts of a radical.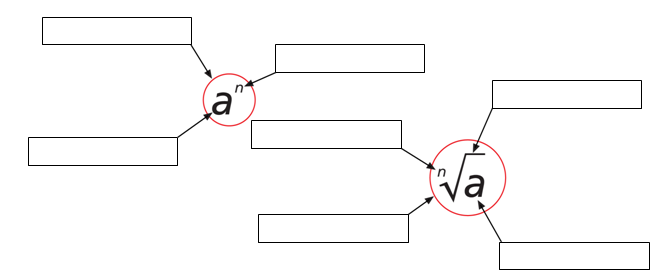
6. Simplify the following expressions. Report answers with positive exponents.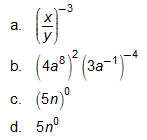
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
Go to “Adding and Subtracting Fractions” to see how to add and subtract common fractions and improper fractions. The concepts of equivalent fractions and lowest common denominator are explained. This lesson also includes math problems and a math game.
Now watch “Multiplying Fractions.”
Materials
You will need the following to complete Math Lab: Powers and Radicals.
- scientific calculator
You worked with volumes of spheres and other 3-D objects in Module 1. While the aim of this lesson is not to revisit volume in particular, you will be working with cube roots and other radicals.
 Read
Read
Go to the textbook to review an example of how to find the radius of a sphere when you are given the volume.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 4: Solving Problems Using the Exponent Laws” on page 241.
In the last lesson you created a chart reviewing the exponent laws. You also added other laws you recently learned. Compare your chart to this one and be sure it is complete. Add one or two examples showing how the law is applied for each of the exponent laws.
|
Exponent Law |
General Case |
|
Product Law |
|
|
Quotient Law |
|
|
Power of a Power |
|
|
Power of a Product |
|
|
Power of a Quotient |
|
|
Zero Exponent Law |
|
|
Integral Exponent Law |
|
Module 2: Roots and Powers
Discover
In this module, you have learned about both radicals and powers. How does a power relate to a radical?
 Math Lab: Powers and Radicals
Math Lab: Powers and Radicals
Go Math Lab: Powers and Radicals, print it (or copy by hand) and complete it.
Once you have completed these questions, use the link below to check your answers. Make any corrections or notes as needed. File this in your binder( course folder).
Module 2: Roots and Powers
Explore
© Laurence Gough/shutterstock
When you are learning to speak a new language, it is natural to continue thinking in terms of your native tongue and then translating it into the words of the new language. Similarly, when someone speaks to you in the new language, you will take a moment to translate what has been said into English before responding.
In this lesson you will explore how powers with rational exponents are like a new language for those who already understand radicals—the native tongue. You will convert between rational exponents and radicals.
Glossary Terms
Add the following term to your "Glossary terms":- rational exponents
-----------------------------------------------------
You saw in Math Lab: Powers and Radicals that powers with rational exponents are related to radicals. For example, you likely noticed that ![]() The pattern you discovered follows the rule
The pattern you discovered follows the rule ![]() where n is a natural number.
where n is a natural number.
 Tips
Tips
Another way to make the connection between powers with rational exponents and radicals is to think that since
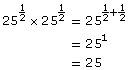
and
![]()
Therefore, ![]()
There are restrictions on the value of the radicand a depending on whether the value of n is even or odd.
Since a negative number cannot be square rooted to give a real solution, the value of a must be positive when n, the index, is equal to 2. This is because neither a negative number nor a positive number can be squared to give a result that is negative. In fact, it is not possible to multiply an even number of like factors together to give a negative product.
For example, 3 × 3 = +9 and (−3) × (−3) = +9, but there is not a number that can be squared to give −9. It is true that 3 × (−3) = −9, but that is not squaring since 3 and –3 are not the same number.
Therefore, when the value of n is even, a must be positive. When the value of n is odd, the value of a can be positive or negative.
Example 1
Use the pattern you discovered to evaluate the following powers.
Solution
 Caution
Caution
It is important to pay attention to the placement of brackets when working with exponents. There is a difference between ![]()
In the first case, the base is −9
![]() that has no real solution.
that has no real solution.
In the second case, the base is 9. The negative is not part of the base since there are no brackets to indicate this. Therefore,
![]()
You are now able to compute powers where the exponent is a fraction of the form ![]() What about rational exponents of the form
What about rational exponents of the form ![]() The following example will show how you can change powers with any rational exponent into an equivalent radical.
The following example will show how you can change powers with any rational exponent into an equivalent radical.
Example 2
Evaluate ![]()
Solution
Method 1

Method 2

Module 2: Roots and Powers
 Share
Share
Compare your answers to the following questions with another classmate or appropriate partner ( if possible). Record any similarities and differences you discussed in your course folder (binder).
Answer the following questions:
1. Describe the differences between method 1 and method 2 as shown in Example 2.
2. List at least one advantage for each method. Which method do you prefer? Use the link provided to check your answers.
You can see that ![]() since both result in the same answer: 64.
since both result in the same answer: 64.
This leads to the rule
![]()
where ![]() suggests you evaluate the nth root first and then apply the exponent m and
suggests you evaluate the nth root first and then apply the exponent m and ![]() suggests you apply the exponent m first and then evaluate the nth root. You will get the correct answer in either case.
suggests you apply the exponent m first and then evaluate the nth root. You will get the correct answer in either case.
 Read
Read
Go to the textbook and work through the following examples. Is there a quick way to remember how to convert a power into a radical, and vice versa? As well, pay attention to how decimals, negative bases, and negative exponents are treated.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Evaluating Powers of the Form ![]() ,” “Example 2: Rewriting Powers in Radical and Exponent Form,” “Example 3: Evaluating Powers with Rational Exponents and Rational Bases,” and “Example 4: Applying Rational Exponents” on pages 224 to 226. Read “Example 3: Simplifying Algebraic Expressions with Rational Exponents” on page 240.
,” “Example 2: Rewriting Powers in Radical and Exponent Form,” “Example 3: Evaluating Powers with Rational Exponents and Rational Bases,” and “Example 4: Applying Rational Exponents” on pages 224 to 226. Read “Example 3: Simplifying Algebraic Expressions with Rational Exponents” on page 240.
 Self-Check
Self-Check
These questions are based on the examples you just read. There may be more than one way of solving these questions. If your method does not match the one provided, check with your teacher to confirm whether your method is appropriate.
Go to the textbook.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Complete the following questions on pages 224 to 226 in your textbook.
SC 1. “Check Your Understanding” question 1.b)
SC 2. “Check Your Understanding” question 1.c)
SC 3. “Check Your Understanding” question 2.a)
SC 4. “Check Your Understanding” question 2.b)
SC 5. “Check Your Understanding” question 3.b)
SC 6. “Check Your Understanding” question 3.d)
SC 7. “Check Your Understanding” question 4.a)
 Try This 1 and 2
Try This 1 and 2
Complete the following in your course folder ( binder).
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 1. Complete “Exercises” questions 4.b, 6.b, 7.e, 9, 10.c, 11.e, 12.f, 13.c, 15, and 19 on page 227 and 228.
TT 2. Complete the following “Exercises” questions 10.a, 10.d, 10.f, 10.g, 15.b, 15.d and 16.c., 16.d on page 242 and 243.
Use the link below to check your answers to Try This 1 and 2.

© Amy Walters/shutterstock
You have now learned a total of eight exponent laws! These include the first five you learned in your previous math courses, as well as the newly learned zero exponent, integral exponent, and rational exponent laws.
How do you know if you have the right answer to a question? If you have completed multiple steps to arrive at the final answer, how do you know you didn’t make a mistake in one of those steps?
When confronted with the task of simplifying an expression involving exponents, you will likely have to apply several of these laws. You will have the freedom to approach the problem in several different (and correct) ways. However, because these problems involve multiple steps, you are at risk to make an error. Examples of errors could include forgetting to reciprocate a base or forgetting to include the negative sign with a base when it is not appropriate to do so.
A simple way to know is to enter the original expression into your calculator and then enter the final answer into the calculator. Compare those results to see if they are the same. If they are not, and you have entered both numbers in a correct manner, then you should check your work for errors. If they are equal, then you have used a correct method!
Identifying Errors
In the last section of this lesson you will analyze some typical student work that contains such errors. Can you detect the errors and, given the chance, advise the student as to how to correct the work?
Example 3
In the following solution, identify the error that was made.
Step 1: 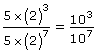
Step 2: ![]()
Step 3: ![]()
Step 4: ![]()
Step 5: ![]()
Solution
The sequence from step 2 to step 5 is correct. Starting with ![]() the quotient law is used to get 10– 4 in step 3. Then the Integral Exponent Law is applied to get the final answer. The error, however, is in the very first step; that is,
the quotient law is used to get 10– 4 in step 3. Then the Integral Exponent Law is applied to get the final answer. The error, however, is in the very first step; that is, ![]() and
and ![]() The student multiplied the 5 to the base 2, but that is incorrect because according to the order of operations, exponents should be treated before multiplication.
The student multiplied the 5 to the base 2, but that is incorrect because according to the order of operations, exponents should be treated before multiplication.
A correct approach would be to deal with the coefficients separately. So,
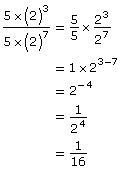
 Try This 3 and 4
Try This 3 and 4
For practice, here are a few error-identification questions. Be sure to identify not only the incorrect work but also explain why the work is incorrect. Then provide the correct solution.
Complete the following in your course folder ( binder).
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 3. Complete “Exercises” questions 18 and 22 on page 228.
TT 4. Complete “Exercises” questions 17.a) and 19 on page 242.
Use the link below to check your answers to Try This 3 and 4.
Possible TT 3 and 4 Solutions
Module 2: Roots and Powers
Connect
 Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under under the Assess tab or by using the Quizzes link under the Activities block. Also, ensure your work in your binder (course folder) is complete.
 Project Connection **NOT ASSIGNED**
Project Connection **NOT ASSIGNED**
In the last Project Connection you learned about binary numbers and how to convert between decimal (base 10) numbers and binary numbers. You also learned that computers use binary numbers to store data, communicate information, and run programs. In this lesson you will see how binary numbers can be used to encode characters on a computer keyboard, not just numbers.
When computers were in the beginning stages of development, there was no standard way of using binary numbers to represent letters. One computer might be programmed to recognize 10010101 as the letter K and another might recognize 01001011 as the same letter. Eventually, computer manufacturers agreed to use a standard code so all computers would assign the same letter for a given binary number. This code is called the American Standard Code for Information Interchange or ASCII.
The ASCII code assigns eight-digit binary numbers to letters and punctuation marks. Each eight-digit or eight-bit number can be stored as a byte. The table shows how some of those numbers are assigned.
|
Binary |
Dec |
Glyph |
|
0100000 |
32 |
|
|
0100001 |
33 |
! |
|
0100010 |
34 |
“ |
|
0100011 |
35 |
# |
|
0100100 |
36 |
& |
|
0100101 |
37 |
% |
|
0100110 |
38 |
& |
|
0100111 |
39 |
‘ |
|
0101000 |
40 |
( |
|
0101001 |
41 |
) |
|
0101010 |
42 |
* |
|
0101011 |
43 |
+ |
|
0101100 |
44 |
, |
|
0101101 |
45 |
- |
|
0101110 |
46 |
. |
|
0101111 |
47 |
/ |
|
0110000 |
48 |
0 |
|
0110001 |
49 |
1 |
|
0110010 |
50 |
2 |
|
0110011 |
51 |
3 |
|
0110100 |
52 |
4 |
|
0110101 |
53 |
5 |
|
0110110 |
54 |
6 |
|
0110111 |
55 |
7 |
|
0111000 |
56 |
8 |
|
0111001 |
57 |
9 |
|
0111010 |
58 |
: |
|
0111011 |
59 |
; |
|
0111100 |
60 |
< |
|
0111101 |
61 |
= |
|
0111110 |
62 |
> |
|
0111111 |
63 |
? |
|
Binary |
Dec |
Glyph |
|
1000000 |
64 |
@ |
|
1000001 |
65 |
A |
|
1000010 |
66 |
B |
|
1000011 |
67 |
C |
|
1000100 |
68 |
D |
|
1000101 |
69 |
E |
|
1000110 |
70 |
F |
|
1000111 |
71 |
G |
|
1001000 |
72 |
H |
|
1001001 |
73 |
I |
|
1001010 |
74 |
J |
|
1001011 |
75 |
K |
|
1001100 |
76 |
L |
|
1001101 |
77 |
M |
|
1001110 |
78 |
N |
|
1001111 |
79 |
O |
|
1010000 |
80 |
P |
|
1010001 |
81 |
Q |
|
1010010 |
82 |
R |
|
1010011 |
83 |
S |
|
1010100 |
84 |
T |
|
1010101 |
85 |
U |
|
1010110 |
86 |
V |
|
1010111 |
87 |
W |
|
1011000 |
88 |
X |
|
1011001 |
89 |
Y |
|
1011010 |
90 |
Z |
|
1011011 |
91 |
[ |
|
1011100 |
92 |
\ |
|
1011101 |
93 |
] |
|
1011110 |
94 |
^ |
|
1011111 |
95 |
_ |
|
Binary |
Dec |
Glyph |
|
1100000 |
96 |
` |
|
1100001 |
97 |
a |
|
1100010 |
98 |
b |
|
1100011 |
99 |
c |
|
1100100 |
100 |
d |
|
1100101 |
101 |
e |
|
1100110 |
102 |
f |
|
1100111 |
103 |
g |
|
1101000 |
104 |
h |
|
1101001 |
105 |
i |
|
1101010 |
106 |
j |
|
1101011 |
107 |
k |
|
1101100 |
108 |
l |
|
1101101 |
109 |
m |
|
1101110 |
110 |
n |
|
1101111 |
111 |
o |
|
1110000 |
112 |
p |
|
1110001 |
113 |
q |
|
1110010 |
114 |
r |
|
1110011 |
115 |
s |
|
1110100 |
116 |
t |
|
1110101 |
117 |
u |
|
1110110 |
118 |
v |
|
1110111 |
119 |
w |
|
1111000 |
120 |
x |
|
1111001 |
121 |
y |
|
1111010 |
122 |
z |
|
1111011 |
123 |
{ |
|
1111100 |
124 |
| |
|
1111101 |
125 |
} |
|
1111110 |
126 |
~ |
You can use the ASCII table and your knowledge of decimal to binary conversions to encode secret messages. The following section outlines the steps for encoding the message “Hello Eva.”
Step 1: Create a chart like the following:
|
Letter |
Decimal Number |
Binary |
Step 2: Write the letters of the secret message in the first column. Note that the chart provides different codes for upper case and lower case letters.
|
Letter |
Decimal Number |
Binary |
|
H |
||
|
e |
||
|
l |
||
|
l |
||
|
o |
||
|
E |
||
|
v |
||
|
a |
Step 3: Use the ASCII table to locate the decimal or binary numbers.
|
Letter |
Decimal Number |
Binary |
|
H |
72 |
1001000 |
|
e |
101 |
1100101 |
|
l |
108 |
1101100 |
|
l |
108 |
1101100 |
|
o |
111 |
1101111 |
|
E |
69 |
1000101 |
|
v |
118 |
1110110 |
|
a |
97 |
1100001 |
Step 4: Express your code in the format of your choice:
72.101.108.108.111.69.118.97
OR
1001000-1100101-1101100-1101100-1101111-1000101-1110110-1100001
At this time, go to the Unit 2 Project and complete the Module 2: Lesson 6 portion of the project.
 Going Beyond
Going Beyond

© andrés arias/shutterstock
If you have ever worked with Internet that was delivered using a satellite, you may have experienced a slight hesitation in the transmission of information. Why is that?
One of the disadvantages of the geosynchronous orbit (an orbit that keeps the satellite at the same place with regards to Earth) is the signal delay.
When a satellite is 22 240 mi away from the surface of Earth and the speed of light is around 186 000 mi per second, there is a delay of around one-quarter of a second from the time a signal is sent up to the satellite to the time the signal is received by an antenna back here on Earth.
Here is the formula that has been developed by scientists:
![]()
t = satellite’s time duration of orbit
d = distance from the centre of Earth
k = a constant
Using this formula, you could find out what the time lag would be with satellites in other orbits. What if, for example, there is a satellite that orbits in 12 hours? Or what about a satellite that orbits in 18 hours? Would the light lag be half as much or something different?
If you know the lag for a 24-hour orbit, you can find the value for k. Then you can use it and the formula to find the lag for other orbits.
|
Duration of Orbit |
Light Lag |
|
24 hours |
0.24 seconds |
|
18 hours |
|
|
12 hours |
Module 2: Roots and Powers
Lesson 6 Summary
In Lesson 6 you investigated the following questions:
- How are powers and radicals related to each other?
- How do you determine and understand error in mathematics?
You began this lesson by completing Math Lab: Powers and Radicals that related powers with rational exponents to radicals. You discovered the rational exponent law that states the following:
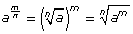
The result of this discovery is that you can evaluate powers by converting them into radicals first.
In this lesson you also identified and corrected errors in calculations involving powers. You learned about common errors that arise from misinterpretations of the exponent laws. You also learned that an easy way to check the answer to a multistep solution is to use a calculator to compare the entered value of the original expression with the value of the final answer.
In the next module you will continue to practise identifying and explaining errors in polynomial multiplication and polynomial factorization.