Lesson 4: Factoring Trinomials of the Form ax^2 + bx + c
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 4: Factoring Trinomials of the Form ax^2 + bx + c |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 3:28 AM |
Module 3: Polynomials
Lesson 4: Factoring Trinomials of the Form ax2 + bx + c
Focus

© Monkey Business Images/shutterstock
From 1930s to the 1950s, rotor machines were state-of-the-art devices used for encrypting and decrypting secret messages. The system used a simple substitution cipher, where each letter was replaced by a different letter based on an algorithm known only to some. The most famous example is the Enigma machine used in World War II.
Times have changed. Nowadays, encryption is used for many things besides secret messages. For example, codes are used in a wide variety of commercial data-storage applications, most prominently in CDs, DVDs, and Blu-ray discs. In fact, polynomial codes are used in these applications! The properties of polynomials that allow you to add, subtract, multiply, and divide also allow a great range of coding options.
In this lesson you will continue to explore factoring strategies. In particular, you will learn how to factor trinomials of the form ax2 + bx + c, where a ≠ 1.
Outcomes
At the end of this lesson, you will be able to
-
model the factoring of a trinomial in the form ax2 + bx + c, concretely or pictorially, and express the polynomial in factored form
-
express a polynomial as a product of its factors
-
factor a polynomial, and verify by multiplying factors
Lesson Questions
-
How is a multiplication array similar to a cipher?
-
How are the coefficients of a trinomial related to the coefficients of its binomial factors?
 Lesson Assessment and Completion
Lesson Assessment and Completion
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Assess tab or by using the Quizzes link under the Activities block.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 3: Polynomials
Launch
Are You Ready?
Complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
1. Arrange the terms into two pairs so that each pair has the greatest possible common factor.a. 2x3, 3x2, 3, 2x
b. 21x3, 2y, 6x2y, 7x
c. 1, xy, x, y
d. 10ax, 4ay, 15x, 6y
a. 2x(x + 1)
b. (x + 3)(x - 2)
c. 3(x + 2)(2x - 5)
3. Find two numbers whose product and sum are indicated in the table. The first row has been done as an example.
|
|
Product |
Sum |
Integers |
|
Example |
10 |
7 |
5 and 2 |
|
a. |
20 |
-9 |
|
|
b. |
-12 |
1 |
|
|
c. |
-60 |
11 |
|
a. 15x2y2 + 25x3y2
b. x2 - 8x - 9
c. 2x2 + 6x - 20
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
Answers
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources either before or after you try the Are You Ready? questions. Your teacher may also direct you to this section to review specific concepts.
Watch the “Mathcast 007 Greatest Common Factor” . You can move through the first examples until you find the ones that cover polynomial CF.
-------------------------------------------------------------------
Watch the “Mathcast 005 Using an Area Model to Illustrate the Multiplication of a Binomial and a Binomial” . Watch the video to see how you can use algebra tiles to model the multiplication of binomials.
-------------------------------------------------------------------
Watch this short video" Factoring Trinomials using the Product Sum method" that gives some help on how to be sure you have the entire set of factors when factoring a trinomial.
Materials
For this lesson, you may wish to use the set of algebra tiles that you borrowed from your teacher or that you created from the Algebra Tiles Template.
Alternatively, you could continue to use the “Arranging Algebra Tiles” applet.
Module 3: Polynomials
Discover
One of the concepts you investigated in the previous lesson was how to use algebra tiles to model the factoring of trinomials.
In this section you will look for patterns in factoring trinomials of the form ax2 + bx + c.
 Math Lab: Factoring ax2 + bx + c
Math Lab: Factoring ax2 + bx + c
Print (or copy by hand) and complete Math Lab: Factoring ax2 + bx + c.
Math Lab: Factoring ax2 + bx + c.
Use the link provided to check your work. *** DO the work before checking - this will lead to much better understanding**
Module 3: Polynomials
Explore

© sonya etchison/shutterstock
The photograph shows a group of students entering a high school. Some might have taken the bus, or perhaps a family member drove some of the students to school. Some of the students may live close enough to the school that they walked.
In other words, the students shown in the photo arrived at the same destination but may have used different methods to arrive.
This analogy is applicable to mathematics. Often there are multiple strategies for solving a problem. Your method may be different from your friend’s method, but both methods lead to the same answer.
This is particularly true of factoring trinomials, where there are many strategies that can be used. In this lesson you will learn these strategies. While you may prefer one strategy more than another, it is important to realize that your preferred strategy may not always be the most effective way to solve each problem. That’s why it is important that you learn several ways to factor a trinomial.
Glossary Terms
Add these terms to your 'Glossary Terms" in your notes:
- decomposition
- inspection
-------------------------------------------------------
FACTORING TRINOMIALS IN THE FORM ax2 + bx + c
VERY IMPORTANT: This skill is perhaps the MOST important skill (** ESPECIALLY METHOD 2**)you will learn in this course. Take TIME ( lots of it) to learn and practice this skill.
Factoring trinomials of the form ax2 + bx + c is different from factoring trinomials of the form x2 + bx + c due to the fact that the leading coefficient is not equal to 1.
There are several strategies for factoring a trinomial of the form ax2 + bx + c. The methods you will learn in this lesson include
Method 1: Area method ( algebra tiles)
Method 2: Decomposition method** the most common process and the one you should spend the most time on**
Method 3: Tic-Tac-Toe method
Method 4: Inspection ( not recommended as a general practice)
 Tips
Tips
Here are two quick tips to help your factoring go smoothly:
-
Always check for a greatest common factor first. It doesn’t take much time, and you’ll appreciate working with smaller numbers.
-
If the terms of a trinomial are scrambled, rewrite it in the form ax2 + bx + c. This is beneficial regardless of which strategy you use.
Method 1: Area Method
![]() Watch and Listen
Watch and Listen
Watch the video “Mathcast 010 Using the Area Model to Factor Trinomials”. This is the same video we looked at in Lesson 3 but you want to start at Example 2 so move the time slider to 3:32. There are three examples to watch here (Example 2 starts at 3:32, Example 3 starts at 5:19 and Example 4 starts at 7:24. As you watch, pay attention to how negative terms in a trinomial are treated in the factoring process and how he uses the zero principle to make the product a rectangle.
----------------------------------------------------------------------

------------------------------------------------------------
The following example shows you how to use algebra tiles and the area method to factor a trinomial of the form ax2 + bx + c.
Example 1
Factor 2x2 – x – 6.
Solution
Step 1: Gather two x2-tiles, one negative x-tile, and six negative 1-tiles.

Step 2: It is not possible to arrange these tiles into a rectangular area. So you will need to use more tiles.
Gather both positive and negative x-tiles, ensuring that you always have one more negative x-tile than positive x-tiles.
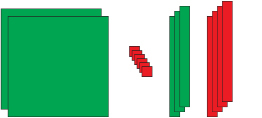
Step 3: Arrange the tiles into a rectangular area.

Step 4: Obtain the dimensions of the rectangle.
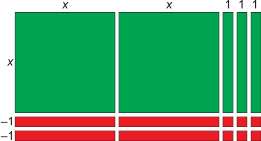
Step 5: Write the dimensions as two binomials.
(2x + 3)(x – 2)
---------------------------------------------------------------------
 Try This 1
Try This 1
Now it's time for you to get some more practice on these types of factoring questions using tiles.
Complete the following questions in your course folder (binder) using algebra tiles. Use the “Arranging Algebra Tiles”” applet as needed but do try hard to do these on your own.
1. Use algebra tiles ( and draw the picture in your binder for future reference) to factor each trinomial.
a. 2x2 + 5x + 3
b. 3x2 + 7x + 4
c. 3x2 + 7x - 6
d. 6x2 + 11x + 4
Possible TT1 ( Try This 1) Solutions
 Self-Check 1
Self-Check 1
SC 1. Use algebra tiles and the area method to factor these questions. As you complete these questions, see if you can figure out a way to know how many positive and negative x-tiles are needed to factor a trinomial with at least one negative term. Try NOT to use the Arranging Algebra Tiles applet.
- 4x2 + 12x + 9
- 3x2 – 10x + 8
- 2x2 + x – 6
Factoring by grouping:
In order to explore the next strategy for factoring trinomials, you need to first consider the factoring of a four-term polynomial.
When factoring a four-term polynomial, you may notice that you can take a common factor out of some of the terms, but not all. If you put the terms into two groups, then you can sometimes take a common factor out of each group.
Example 2
Factor 6x2 + 2y + 15x2y + 5y2.
Solution
Step 1: Group the first pair and the last pair of terms.
(6x2 + 2y) + (15x2y + 5y2)
Step 2: Take the greatest common factor out of each group. So factor a 2 out of the first two terms and factor a 5y out of the last two terms.
= 2(3x2 + y) + 5y(3x2 + y)
The key is to arrange the terms so that you have the same factors left in the brackets. See how, in the previous example, both brackets have the binomial (3x2 + y).
Step 3: When the binomials are the same, the binomial is considered a common factor and you can divide it from each term in the expression.

= (3x2 + y)(2 + 5y)
So,
6x2 + 2y + 15x2y + 5y2 = (3x2 + y)(2 + 5y)
Step 4: You can verify the result by multiplying the factors.
(3x2 + y)(2 + 5y) = 3x2(2 + 5y) + y( 2 + 5y)
= 6x2 + 15x2y + 2y + 5y2
( The order of the terms is different but it is the same polynomial expression)
 Self-Check 2
Self-Check 2
SC 2. Apply the method of factoring by grouping to the following expressions.
- x3 + x2 + 4x + 4
- 2ab + 2b2 – 3a – 3b
Method 2: Factoring by Decomposition
** AGAIN - IT CANNOT BE STATED ENOUGH HOW IMPORTANT THIS SKILL IS FOR SUCCESS IN HIGH SCHOOL MATH**
Recall that multiplication and factoring are inverse operations. When you multiply two binomials, for instance, your result may be a trinomial. To recover those binomials, you can factor the trinomial.
In the Discover section of this lesson you investigated the multiplication of various binomials to discover a pattern for factoring trinomials of the form ax2 + bx + c.
Retrieve the Math Lab: Factoring ax2 + bx + c results that you completed in the Discover section. Look at the second row of your table.

It is also important to the discovery of a factoring technique that you notice another pattern. The leading coefficient and the constant (in the second and fifth columns) are equal to the product of the two x-terms (in the third and fourth columns). In other words, 2 × (–15) = –30 and 10 × (–3) = –30.
The factoring method of decomposition involves the breaking—or decomposing—of the middle term of a trinomial into two terms. Those terms must have a sum equal to the middle term of the trinomial. At the same time, the product of those terms must be equal to the product of the leading coefficient and the constant.
The decomposed polynomial can then be grouped and factored by common factors.
Example 3
Factor 2x2 + 7x – 15 by decomposition.
Solution
Step 1: Find two numbers whose product is equal to the product of 2 × (–15) and whose sum is equal to 7. Note this is DIFFERENT that trinomials we learned about in Lesson3. The product comes from the first term coefficient multiplied by the constant term.

Step 2: Use a product - sum table to list the factors and the sum of each set of factors.
Select the pair that can give you the same number as the middle term of the trinomial.
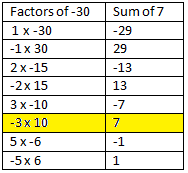
Step 3: Rewrite the trinomial as a four-term polynomial. Do this by breaking the middle term into the two terms found in the previous step.
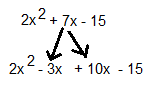
Step 4: Group the first two terms and the last two terms so that the expression is the sum of two binomials. ( This is grouping that you just practiced above).
= (2x2 - 3x) + (10x – 15)
Step 5: Factor out the greatest common factor from each group of terms.
= x(2x - 3) + 5 (2x - 3)
Step 6: Factor out the common binomial.
=(2x-3) (x + 5)
![]() Watch and Listen
Watch and Listen
For further explanation on the factoring strategy of decomposition, here are two videos to watch:
1. Watch the video "Mathcast 011a - Using Algebraic Patterning to Factor a Trinomial "where he combines common factoring and factoring by grouping/decomposition in one question.

2. Watch a second video “Mathcast 11b Using Algebraic Patterning to Factor a Trinomial ‘Decomposition.’” This videos shows three skills: Finding the Product/Sum numbers, Common Factoring and then Factoring by Grouping/Decomposition.
![]() Read
Read
The following example demonstrates how a trinomial is factored by decomposition. As you read, look for the answers to these questions:
- What is the first thing you should do when you approach a factoring task?
- How can you systematically determine the numbers that meet the product-sum criteria?
| Foundations and Pre-Calculus Mathematics 10( Pearson) Read " Example 4: Factoring a Trinomial by Decompostion on pages 175 and 176. |
![]() Try This 2
Try This 2
Complete the following in your course folder ( binder).
LOTS of practice is needed here so this becomes a skill you are VERY good at.
SPEND LOTS OF TIME ON THIS (are you getting the hint how important this is - haha).
Foundations and Pre-calculus Mathematics 10 (Pearson)
Questions 19, and 20.a), 20.c), 20.e), 20.f), on page 178
Use the link below to check your answers to Try This 2.
Possible TT2 (Try This 2) Solutions
![]()
Foundations and Pre-calculus Mathematics 10 (Pearson)
page 177 - 178 # 12, 13, 15, and 18.
Mathematics 10C Learn EveryWare © 2010 Alberta Education
Method 3: Tic-Tac-Toe Method
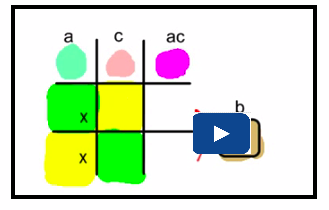
You can also apply the concepts of decomposition using a graphic organizer to help you keep track of your work. This graphic organizer is a 3 × 3 multiplication array, similar to a tic-tac-toe square.

© Helder Almeida/shutterstock
Example 4
Factor 3x2 – 8x + 4.
Solution
Step 1: The first part is similar to decomposition. Find two numbers whose product is equal to the product of the first term times the third term or 3 × 4, or 12, and whose sum is equal to the middle term or –8.
Use a table to consider the possibilities. ** Think - since the product is positive and the sum is negative, BOTH numbers need to be negative.
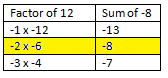
The numbers are –2 and –6, since the product is (–2) × (–6) = 12 and the sum is (–2) + (–6) = –8.
Step 2: Construct a 3 × 3 array as shown. Place the x2-term in the centre square. Place the constant in the last square in the bottom row.
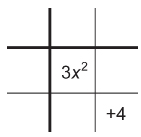
Step 3: Place an x-term in the last square in the middle row and an x-term in the second square of the last row. These x-terms should have coefficients equal to the numbers determined in step 1.
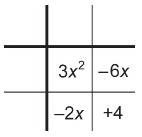
Step 4: Above each of the second and third columns, determine the GCF of the terms in the column. Ignore any negative signs for now.
3x2 = 3 × x × x
2x = 2 × x
GCF = x
6x = 2 × 3 × x
4 = 2 × 2
GCF = 2
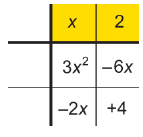
Step 5: Next to each of the second and third rows, determine the GCF of the terms in the row. Ignore any negative signs for now.
3x2 = 3 × x × x
6x = 2 × 3 × x
GCF = 3x
2x = 2 × x
4 = 2 × 2
GCF = 2
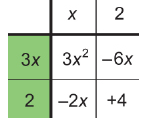
Step 6: Consider the signs of the terms in the top row and the left column. Remember that the product of two terms with the same sign is positive, while the product of two terms with opposite signs is negative.
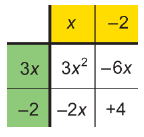
Since 3x2 is positive, x and 3x can remain positive. On the other hand, if those terms are positive, then the 2 in the left column and the 2 in the top row must be negative in order to justify the –6x and –2x.
The factors are (x – 2) and (3x – 2).
Check by multiplying.
( x- 2) ( 3x - 2) = x ( 3x - 2) - 2( 3x - 2)
= 3x2 - 2x - 6x + 4
= 3x2 - 8x + 4
 Watch and Listen
Watch and Listen
For further explanation on the tic-tac-toe method,
1. Go to this site that has several more problems solved.
2. Watch the video "Factoring Trinomials - Tic Tac Toe method"
 Self-Check 3
Self-Check 3
SC 3. Practise using the method of decomposition or the tic-tac-toe variation of this method to factor the following.
- 2x2 + 11x + 12
- 5x2 - 7x + 2
Mathematics 10C Learn EveryWare © 2010 Alberta Education
Method 4: Factoring by Inspection
Another way of factoring trinomials is by inspection. This method is based on reasoning and educated guesswork. This method can be done quickly as long as the coefficients are relatively small and have few factors.
The method of inspection is based on a consideration of the factors of the x2-term and the constant. Through trial and error, factors are accepted or rejected. As a result, it is important to check your final answer by multiplying the factors to see if the trinomial is recovered.
 Watch and Listen
Watch and Listen
Watch the video titled “Factoring by Inspection” to see a demonstration of how to use the method of inspection to factor the trinomial 2x2 - 7x + 6. Pay careful attention to how the coefficients of the trinomial are used to determine the coefficients of the binomial.
![]() Read
Read
The following example show how to complete a factoring question by Inspection or by "Using logical Reasoning".
| Foundations and Pre-Calculus Mathematics 10( Pearson) Read " Example 3: Factoring a Trinomial Using Logical Reasoning on page 172 - 173. |
 Try This 3
Try This 3
Practice applying the method of Inspection or Logical reasoning to the questions below.
Why would this process be appropriate for these questions?
Factor using inspection and then verify by multiplying
1. 2m2 + 3m - 9
2. 12y2 + y - 1
3. 2x2 - x - 1
4. 3x2 + x - 2
Possible TT3 ( Try This 3) Solutions
Common Errors
As you practice factoring using the methods that you have learned in this lesson, you should be aware of some common errors that can occur. Some of these errors are due to inattention to details but do not imply student misunderstanding. Other types of errors reveal a misconception of the recently learned math principles.
The following examples show how a student may factor a polynomial using the methods learned in this lesson.
 Self-Check
Self-Check
SC 4. Study the solutions and identify the error that has been committed. Then correct the error and complete the solution.
- Factor 2x2 + 7x + 6. Find two numbers whose product is 6 and whose sum is 7. The numbers are 6 and 1.
Therefore, the binomial factors are (x + 6)(x + 1).
Since the leading coefficient is 2, the final factored form is 2(x + 6)(x + 1). - Factor 6x2 + 11x – 10. Find two numbers whose product is –60 and whose sum is 11.
The two numbers are 15 and –4.
Set up the tic-tac-toe grid.
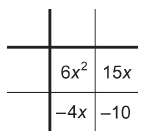
Determine the GCF for each column of terms and row of terms.
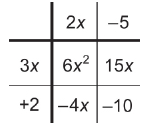
The factors are (2x – 5)(3x + 2).
 Try This 4
Try This 4
Be sure to identify the error and also to correct it. As you examine the solutions, focus on this question: During what phase of a solution are errors usually found? Are the errors found in the initial steps, the last steps, or the intermediate steps?
Complete the following in your course folder ( binder) and use the link provided to check your work.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Questions 16a and 17 on page 178
Possible TT4 ( Try This 4) Solutions
Mathematics 10C Learn EveryWare © 2010 Alberta Education
Module 3: Polynomials
Connect
In this lesson you learned strategies that can be used to factor trinomials of the form ax2 + bx + c. Take the opportunity now to update your Factoring Strategies document ( This should have been saved from Lesson 3 or copied by hand). Add information to your document that will help you to remember the steps of each method. Also, add notes that will help you recognize which strategy to use in a given situation.
In the final Try This section of this lesson, you examined ways in which errors can be made in the factoring of a polynomial. You may have noticed some errors in your classmates’ work as well as your own. It is a good idea to include notes about such errors in your chart as a reminder of how to avoid these types of error.
As you continue to learn new strategies for factoring different types of polynomials, continue to add to this chart. By the end of this module, you will have an invaluable study tool that can help you review some of the major outcomes you have learned.
 Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Assess tab or by using the Quizzes link under the Activities block. Also, ensure your work in your binder (course folder) is complete.
----------------------------------------------------------------------------------------
 Project Connection ** NOT ASSIGNED**
Project Connection ** NOT ASSIGNED**
The following photo shows the Navajo Code Talker monument in Window Rock, Arizona, USA. This photo is a clue to the Project Connection for this lesson.

You can use trinomial factoring as the basis of a cipher. Go to the Unit 2 Project. Complete the Module 3: Lesson 4 portion of the project to decipher the names of two actors who starred in a movie about secret codes. Use their names as keywords in your search engine to discover the name of the movie.
 Going Beyond
Going Beyond
In the Going Beyond section of the previous lesson, you learned how to use a graphing calculator to verify the factors of a polynomial. Now you will investigate how the graph of a trinomial of the form ax2 + bx + c can help you to identify its factors.
Factor the trinomial x2 + 2x – 15.
On a graphing calculator, complete the following steps.
Step 1: Enter Y1 = x2 + 2x – 15.

Step 2: Execute the Graph command. This type of graph is called a parabola.
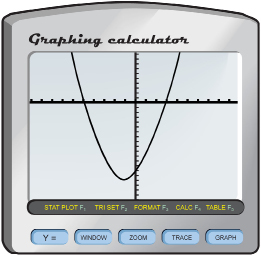
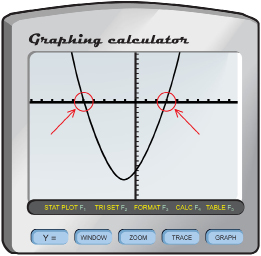
Step 3: Determine the points on the graph where the parabola intersects the horizontal axis. These are called the x-intercepts.
Answer the following questions. You should save your answers to your course folder. Also, check with your teacher to see if you are required to submit the answers to these questions for marks.
-
How do the x-intercepts compare with the coefficients of the binomial factors of x2 + 2x – 15?
-
Repeat steps 1 and 2 using the trinomial 2x2 + 15x + 7. How do the x-intercepts compare with the coefficients of the binomial factors of 2x2 + 15x + 7?
-
Graph the following trinomials. Try to determine the factors of each trinomial by looking only at the graph.
- x2 – 6x + 5
- 2x2 – 13x + 6
Share the answers to the questions with a partner. Find out how your partner responded to the questions and also if he or she noticed the same results as you did.
You will have the opportunity to further explore this relationship between a graph and a trinomial in future math courses.
Module 3: Polynomials
Lesson4 Summary
In Lesson 4 you investigated the following questions:
-
How is a multiplication array similar to the basis of many codes?
-
How are the coefficients of a trinomial related to the coefficients of its binomial factors?
In this lesson you learned how to factor trinomials of the form ax2 + bx + c, where a ≠ 1. Just as you can use a multiplication array to multiply binomials (see Lesson1), you can also use the arrays to factor trinomials.
In this way, the multiplication array is similar to a cipher. To encode a message, for example, the letters of the plaintext are scrambled in a prescribed way. To decode the message, the letters of the ciphertext must be de-scrambled in a way that is precisely the reverse of how it was encoded.
Likewise, you discovered in this lesson that in order to factor a trinomial, you must first break the x-term into two terms. Those terms are then placed centrally in the array. Then you determine the greatest common factors of each column and row to obtain the factors along the top row and left column. This procedure is precisely the reverse of the binomial multiplication procedure using the same array.
Besides using arrays, decomposition can be used to factor trinomials. With decomposition, you can “decompose” or break apart the middle term based on the determination of two numbers. For the trinomial ax2 + bx + c, these numbers must have a product equal to a × c and a sum equal to b.
Another way to factor a trinomial is by inspection. This strategy is based on educated guesswork. However, knowledge of how the coefficients of the trinomial relate to the coefficients of the binomial helps you use this factoring strategy effectively. For example, the following expression shows the proper factoring of the trinomial 2x2 - 7x - 4:
2x2 – 7x – 4 = (2x + 1)(x – 4)
Note that the coefficient of the x2-term in the trinomial is equal to the product of the first terms (or x-terms) of the binomials. Also notice that the constant –4 is equal to the product of the constants in the binomials: 1 × (–4).
In the next lesson you will consider ways to factor special polynomials. These polynomials are deemed special because there are ways to factor them based on interesting patterns. You will have the opportunity to discover these patterns before exploring how these patterns can be developed into factoring strategies.