Lesson 4: General Form and Slope-Point Form
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 4: General Form and Slope-Point Form |
| Printed by: | Guest user |
| Date: | Tuesday, 4 November 2025, 3:43 AM |
Module 5: Linear Functions
Lesson 4: General Form and Slope-Point Form
Focus

© Pete Saloutos/20637776/Fotolia
In the Summer Olympics, aquatic disciplines include swimming, diving, synchronized swimming, and water polo.
Consider the similarities and differences between synchronized swimming and relay swimming. Both competitions take place in a swimming pool and both involve teams of competitors. However, Olympic synchronized swimming is not open to men, whereas the relay events involve teams of women as well as teams of men.
Also, synchronized swimming is a judged competition where teams earn scores, whereas relay swimming is a race. In other words, the relay race is based on fastest times while synchronized swimming is based on both technical and aesthetic merits. The relay swimmer will adopt the most practical form to achieve the quickest time; the synchronized swimmer will work with her teammates to execute a performance that includes all the required components in a creative and artistic manner.
In mathematics you will also find different forms to express a linear function. In Lesson 3 you learned about the slope-intercept form. You will recall that this form is practical for obtaining the slope and y-intercept of a linear function. You may also recall how it was useful for graphing.
In this lesson you will learn how to express a linear function in other forms and from one form to the other. Just as some people prefer the excitement of relay competition and others enjoy the artistry of synchronized swimming, you may prefer to use some forms of linear functions for graphing and others for determining points and slopes.
Outcomes
At the end of this lesson, you will be able to
-
express a linear relation in different forms and compare the graphs
-
rewrite a linear relation in either slope-intercept or general form
-
identify equivalent linear relations from a set of linear relations
Lesson Questions
-
How are the general, slope-intercept, and slope-point forms different from each other?
-
Why are there multiple ways of expressing linear functions?
 Assessment
Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Activities block on the left in moodle or under the Assess tab.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 5: Linear Functions
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your binder. If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
Lesson 4: Are You Ready? ** spend significant time on 3 and 4**
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
Answers
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources either before or after you try the questions in Are You Ready? Your teacher may also direct you to this section to review specific concepts.
--------------------------------------------------------------------------------------------------------------------------------------
Use the “Slope-Intercept Form: y = mx + b” video to review some of the concepts covered in Lesson 3.
Go to “Determining the Equation of a Line.”
---------------------------------------------------------------------------------------------------------------------------------
Use the “Graphing Linear Equations Using the Linear Function Explorer” interactive applet to review how the equation of a linear relation in slope-intercept form relates to its graph.
-------------------------------------------------------------------------------------------------------------
Lastly, go to “Formula” to review the definition of formula and how to rearrange formulas. In the Example section, you will see how the width variable in the perimeter formula can be isolated by balancing both sides of the formula. There is also a second example that shows how the radius variable in the circumference formula can be isolated.
----------------------------------------------------------------------------------------------------------------
If you would like a more thorough review to prepare for this lesson, refer to the Explore sections of the following lessons:
-
Module 4: Lesson 4
-
Module 4: Lesson 5
-
Module 5: Lesson 1
Discover
 Math Lab: Linear Forms
Math Lab: Linear Forms
Go Math Lab: Linear Forms, print it (or copy by hand) and complete it.
Math Lab: Linear Forms
You will need to use the “Desmos Calculator” site to complete the Math Lab.
Once you have completed these questions, use the link below to check your answers. Make any corrections or notes as needed. File this in your binder( course folder).
 Self Check 1 -2
Self Check 1 -2
Study the following graph and respond to the questions provided to check that you understood the math lab work.
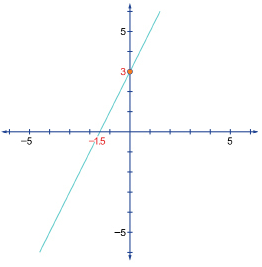
|
y = 2x + 3 |
y−y1 = m(x - x1) y − 3 = 2(x - 0) y − 3 = 2x |
2x − y + 3 = 0 |
1. Do the three equations shown in above represent the same relationship? Explain.
2. How could you get one equation from question 1 to look the same as one of the other equations? Choose two equations, and show the steps you would use to convert one into the other.
Answers
Mathematics 10C Learn EveryWare © 2010 Alberta Education
Module 5: Linear Functions
Explore
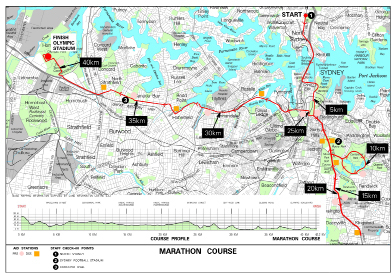
Creator: Sydney Organising Committee for the Olympic Games. © Sydney Olympic Park Authority.
The marathon is a long-distance foot race. In the Olympics, the official distance of the marathon is 42.195 km (or 26 mi and 385 yards). The design of a marathon course depends on several factors. Many courses minimize the number of hills and tight corners in order to make it easier for the athletes to run fast times. The way that a course is designed may also be based on how convenient it is for spectators and television crews to view the race. Since the host city is different from one Olympics to the next, the marathon course is also different at each Olympics. The one thing that remains the same, however, is the distance.
In Lesson 3 you learned to describe a linear function using the slope-intercept form, y = mx + b. In this lesson you will learn about two other forms. While all of these forms are different in appearance, like the Olympic marathon courses, they can all be used to describe the same linear function!
Glossary Terms
Add these terms and their definitions to your "Glossary Terms" section in your notes. You may also want to add examples that demonstrate how each term is applied.
- general form
- slope-point form
- standard form
-----------------------------------------------------------------------------------------------------------------------------------------
Slope-Point Form
In the last lesson you learned to construct the equation of a line using its slope and y-intercept. You can actually use any point on a line to construct the equation of a linear function.
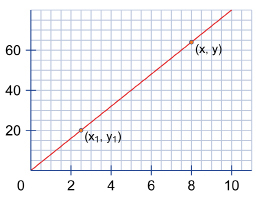
Recall the slope formula for determining the slope of a line with points at (x1, y1) and (x2, y2):
![]()
Examine the line in the slope-point form graph. If a line passes through the point (x1, y1), then you can take any other point on that line (x, y) to determine the equation of the line. You will do this by using the slope formula:
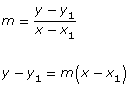
This form for the equation of a linear function is called slope-point form.
 Read
Read
The following example demonstrates how the equation of a linear function can be expressed in slope-point form. As you work through the example, focus on the order of the steps for converting an equation in slope-point form to slope-intercept form.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 2: Writing an Equation Using a Point on the Line and Its Slope” on pages 368. Verify the equation with your calculator.
 Self-Check 3
Self-Check 3
SC 3. The graph of a line that passes through the point (8, 3) with a slope of ![]() is shown.
is shown.
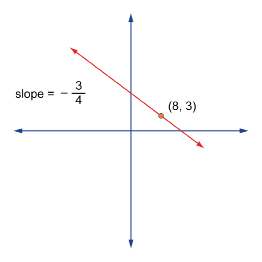
- Write the equation of the line in slope-point form.
- Convert the equation in part a. into slope-intercept form.
General Form
Another way to express the equation of a line is called general form. The general form of a graph is written as ![]() where A is a whole number, B and C are integers, and A and B cannot both be equal to zero.
where A is a whole number, B and C are integers, and A and B cannot both be equal to zero.
|
To ensure that an equation is in correct general form, make sure the coefficient in front of the x in positive and that none of the coefficients are fractions. To do this, multiply each side and each term by a number that changes the coefficients to match these restrictions. |
Retrieve your tables from Math Lab: Linear Forms. Check the last column of each table for examples of linear functions written in general form. Compare the general form to the other forms of linear functions.  Think about the following questions:
Think about the following questions:
1. In what ways is the general form different from the other forms? In what ways is the general form similar to the other forms?
2. What are the benefits of expressing a linear function in general form?
3. Select equations from the tables in Math Lab: Linear Forms to show how you can convert from
a. slope-intercept form to general form
b. general form to slope-intercept form
Possible Solutions are:
1. The general form has one side of the equation as 0; the other forms have x and y on opposite sides of the equal sign. The general form is similar in that its graph is also a line and it has x, y, and constant terms.
2. You can easily find two points to graph. The first point can be found by using x = 0 and solving for y; the second point can be found by using y = 0 and solving for x.
3. a. Any slope-intercept form can be transformed to general form using these steps.
y = mx + b
y – y = mx + b – y **Subtract y from both sides**
0 = mx – y + b ** We just change the letters to match general form
0 = Ax + By + C ** if there are any fractions, we multiply every term by the
lowest common denominator and if A is negative, we
multiply every term by -1**
ex. y = -1/2x + 5
y - y = -1/2x + 5 – y
0 = -1/2x – y + 5 ** since the coefficient in front of x is a fraction AND is
negative, we multiply every term by -2
-2(0) = -2(-1/2x) – (-2)y + -2(5)
0 = x + 2y - 10
b. Any general form can be transformed into slope-intercept form using these steps.
Ax + By + C = 0
Ax – Ax + By + C – C = 0 – Ax – C **Subtract the Ax and C to leave the By term on the left**
By = -Ax – C ** divide every term by B**
Y = -A/B x + -C/B
![]() Read
Read
Go to your textbook to find out how to convert the equation of a linear function into general form. As you read, find out the answers to these questions:
- How do you know by what number you need to multiply both sides of the equation?
- How do you know which side of the equation in which to collect the terms?
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Rewriting an Equation in General Form” on page 379.
Module 5: Linear Functions
Did You Know?
A variation of general form that you will see in the next module is called standard form. The standard form of the equation of a line is Ax + By = C, where A, B, and C are integers and A and B cannot both be equal to zero.
 Self-Check
Self-Check
SC 4. Convert the following equations into general form.
You can also convert an equation in general form to slope-intercept form. This is useful if you wish to identify the slope or y-intercept of a function prior to graphing it. Study the next example to see how this is done.
Example
A linear function is described by the equation 4x − 3y + 12 = 0. Identify the slope and y-intercept of the graph.
Solution
You can rearrange the equation into slope-intercept form in order to identify the slope and y-intercept.
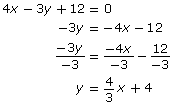
The slope is ![]() and the y-intercept is 4.
and the y-intercept is 4.
Once you have determined the slope and the y-intercept, you can then sketch an accurate graph of the linear function. In the next lesson you will learn strategies for graphing linear functions in general form. One strategy will be to rearrange the equation into slope-intercept form first.
You have now learned about three ways of expressing the equation of a linear function. In this next Self-Check problem, you have an opportunity to work with each one.
 Self-Check
Self-Check
SC 5. The following graph shows the progress of a person who is walking his dog.
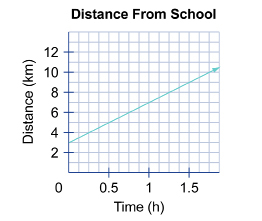
- State the coordinates of two convenient points on the line.
- Use the slope formula to determine the slope of the line.
- Write the equation of the line in slope-point form using one of your points from question a.
- Convert the equation into slope-intercept form.
- State the coordinates of the y-intercept, and explain what the y-intercept means.
- Convert the equation into general form.
You have studied slope-intercept, slope-point, and the general form of a linear function. Two linear functions are equivalent if they have the same slope and pass through the same point. Equivalent forms will have the same slope and y-intercept.
 Try This 1 - 2
Try This 1 - 2
Print (or copy by hand) and complete the following in your course folder binder.
Use the link below to check your answers to Try This 1 - 2.
 Watch and Listen
Watch and Listen
Go to the following site to watch a video on converting forms.
-----------------------------------------------------------------------------
![]()
Go to the following site to look at a few more examples. Scroll to the bottom and do the short self test there.
Module 5: Linear Functions
Connect
 Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Quizzes link to the left in moodle or under the Assess tab and ensure your work in your binder (course folder) is complete.
 Project Connection **NOT ASSIGNED**
Project Connection **NOT ASSIGNED**

Stockbyte/Thinkstock
Retrieve your results from the Math Lab: Bungee Jump Simulation that you completed in the Project Connection for Lesson 3.
In that Math Lab you conducted a bungee simulation using a fashion doll or action figure. You constructed a graph that showed the drop distance compared to the number of elastics bands used to create a bungee cord.
You then constructed a line of best fit and determined the equation of the line in slope-intercept form.
Go to the Unit 3 Project and complete both Part A and Part B of the Module 5: Lesson 4 component of the project.
 Going Beyond
Going Beyond

© Nicholas Piccillo/19345193/Fotolia
In wrestling, there are many ways of scoring points against your opponent. There are points associated with takedowns, escapes, reversals, near falls (when a wrestler almost pins an opponent to the mat), and penalty points.
Some high school wrestlers are successful because they have focused their training on specific manoeuvres in a few of these areas. As a wrestler progresses and encounters tougher competition at the collegiate and even Olympic levels, it is imperative that he or she becomes proficient in all areas in order to experience success.
In this lesson you have learned three ways of expressing a linear equation. There are other ways to write a linear equation. Find these other ways by performing an Internet search. You may want to type the keywords “ways to express a linear equation.” Show an example of each linear equation you find, and provide the information needed to be able to express a linear equation in that form.
Save your findings in your course folder.
Module 5: Linear Functions
Lesson 4 Summary
In this lesson you investigated the following questions:
- How are the general, slope-intercept, and slope-point forms different from each other?
- Why are there multiple ways of expressing linear functions?
There are multiple ways of representing the equation of a linear function. In Lesson 3 you studied the slope-intercept form. In this lesson you examined the slope-point form and the general form.
Here is a nice graphic to summary how to change between the forms.
In the Going Beyond section of this lesson, you may have discovered even more ways that a linear equation can be expressed. Besides learning about the different forms, you also learned how to convert between forms. Specifically, you learned how to convert a linear equation from slope-intercept and slope-point forms into general form and from general form to slope-intercept form. Each method of representing a linear equation has its benefits. Both the slope-intercept form and the slope-point forms are useful for graphing since you can easily extract a point and the slope from each form.
General form is different from the slope-intercept and slope-point forms in two key ways. First, the coefficients are integers or whole numbers. This means that equations in general form will not contain fractions or decimals. Second, the terms of an equation expressed in general form will all be on the same side of the equation. While the slope and y-intercept are not directly given in general form, you can still determine those properties of the linear function by rearranging the equation into one of the other forms.
It is helpful to have multiple ways of representing an equation since this allows you the flexibility of interpreting and presenting a linear relation based on the information that is available. In this lesson you have learned to identify equivalent linear relations from a set of linear relations. One approach is to rearrange equations into slope-intercept form. You can then compare the slopes and intercepts. In the next lesson you will apply the information about the three equations you learned, and you will create graphs for all three equation types.