Lesson 2: Modelling Linear Systems
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 2: Modelling Linear Systems |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 5:23 AM |
Module 7: Systems of Linear Equations
Lesson 2: Modelling Linear Systems
Focus

Creatas/Thinkstock
Volunteerism is the act of serving others without pay or material gain. When you volunteer, either as an individual or as part of a team, you are freely giving your time and talents to a worthwhile cause. Volunteer opportunities for young and old can be found in hospitals, children’s camps, music and arts festivals, charities, and environmental organizations, to name just a few. You can also volunteer closer to home by doing yard work for an elderly neighbour, tutoring a younger student, or coaching a community team.
Volunteering is a productive way to spend your leisure time. Even though you do not receive financial compensation for your service, volunteering offers other valuable benefits. These benefits include finding out about different career paths, gaining work experience, learning new skills, and making connections with other people.
In this lesson you will continue to study linear systems. You will analyze information and write linear equations to model problems. Many of the math problems that you will encounter in this lesson are based on actual volunteer projects and volunteerism in general. Perhaps you will be inspired to help out in your own community!
Outcomes
At the end of this lesson, you will be able to
- model a situation using a system of linear equations
- relate a system of linear equations to the context of a problem
Lesson Questions
- How do you decide what parts of a problem should be represented by variables?
- How do you organize the information you need to create a linear system?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Activities block on the left in moodle or under the Assess tab.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 7: Systems of Linear Equations
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your binder. If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
Answers
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources either before or after you try the questions in Are You Ready? Your teacher may also direct you to this section to review specific concepts.
For a review, visit “Converting to Slope Intercept Form” to see how you rearrange an equation into y = mx + b form.
---------------------------
For a review of writing a mathematical equation and solving multi-step equations, have a look at the
“Solving Systems of Equations” video.
--------------------------------------
Then read the following.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Determining Intercepts, Domain, and Range of the Graph of a Linear Function” on page 314.
Module 7: Systems of Linear Systems
Discover
 Math Lab: Pennies and Paper Clips
Math Lab: Pennies and Paper Clips
Go Math Lab: Pennies and Paper Clips, and complete it.
Math Lab: Pennies and Paper Clips
Once you have completed these questions, use the link below to check your answers. Make any corrections or notes as needed. File this in your binder( course folder).
Math Lab Answers
Mathematics 10C Learn EveryWare © 2010 Alberta Education
Module 7: Systems of Linear Equations
Explore

© bawinner/3153392/Fotolia
Habitat for Humanity is a non-profit organization whose mandate is to build affordable housing for people all over the world. The objective is accomplished through the co-operation of volunteers who donate their labour in the construction of each house. The houses are then sold for the same amount as the cost of the materials so that no profit is made. Families who qualify to receive a Habitat for Humanity home are selected based on their need for shelter, their ability to pay for the cost of the materials, and their ability to contribute their own labour (approximately 500 hours) into the construction of the house.
The building of a house begins with the construction of a solid foundation. There are many types of foundations and different techniques for constructing them. Regardless of the type of foundation, however, it is important that proper techniques are applied to make certain that the foundation is strong. Such a foundation will ensure the longevity of the house.
In this lesson you will be building the foundation for problem solving. You will study problems and develop techniques for modelling those problems with linear equations. Just like in house construction, it is important that you obtain the correct initial equations to ensure correct solutions.
 Share 1 - 2
Share 1 - 2
Work with a partner (if possible) to find a solution to the following problem. Write down the steps you followed. If there are places in the solution process where you have estimated numbers, please include an explanation of why you chose those numbers.
1. Andrea has a bag of coins. There are 32 coins altogether, consisting of quarters and dimes. The total value of the coins is $5.90. Determine the number of quarters and the number of dimes in the bag.
2. Now find a different partner to work with than the partner you worked with in question 1. Share your strategy for solving the problem in question 1. In your discussion, be sure to address the
- similarities and differences between your approaches
- efficiency and simplicity of each approach
- advantages and drawbacks of each approach
Add the points of discussion to your work and solution to the problem.
--------------------------------------------------------------------------------------------
Many problems can be modelled by a system of linear equations. In this lesson you will focus on problems that involve two unknown quantities. Every problem is different and may require a slightly different approach. There are, however, certain guidelines that can help you to organize the presented information, to represent the situation mathematically, and to solve for the unknown quantities.
The following example shows how question 1 of the Share activity can be modelled by a system of linear equations. The emphasis in this lesson will be to use linear systems to model situations. The emphasis in later lessons will be to solve these systems using various graphical and algebraic techniques.
As you read through the example, focus on the approach to modelling.
Example
Andrea has a bag of coins. There are 32 coins altogether, consisting of quarters and dimes. The total value of the coins is $5.90. Determine the number of quarters and the number of dimes in the bag.
Solution
Let q = number of quarters.
Let d = number of dimes.
number of coins :
d + q = 32
value of coins:
0.1d + 0.25q = 5.90
 Try This 1 - 6
Try This 1 - 6
Answer the following questions in reference to the question above:
TT 1. What clue in the problem suggests that the two unknowns are number of quarters and number of dimes? Where is this clue found in the problem?
TT 2. What do you notice about how the variables are defined in this example?
TT 3. Explain how it might be confusing if the variables were defined instead as the following:
Let x = quarters.
Let y = dimes.
TT 4. Why is it a good idea to begin modelling by defining variables?
TT 5. Explain the significance of each equation.
TT 6. How would you use a graphing method to solve this problem? How do you deal with the fact that the variables are not x and y?
There are many types of situations that can be modelled and solved by a linear system. For example, problems involving mixtures, costs, perimeter, and rates are situations that can be represented by a linear system.
In the remainder of this lesson, you will explore these different types of situations and investigate how you can model them with linear systems.
 Try This 7 - 9
Try This 7 - 9
Complete the following in your course folder ( binder).
Try This 7 - 9 Questions
Use the link below to check your answers to Try This 7 - 9.
Possible TT7-9 Solutions
In the next section you will consider strategies outlined in your textbook.
As you read, think about how the presented strategy can help you with the previous task of modelling equations for Try This 7 - 9.
 Read
Read
Your textbook contains several examples of how to use linear systems to represent situations similar to the ones presented above. Go to your textbook now to review those examples. Look only at the setup of the problem. Do not worry at this time about how to solve the systems.
As you read, create a table similar to the one below. Describe key steps in modelling a problem, and then explain the purpose of those steps.
|
Description of Step |
Purpose |
|
|
|
|
|
|
|
|
|
For example, one step that is common to all problems is the definition of variables. The purpose of this step is so that you can use those variables to write mathematical equations.
Foundations and Pre-calculus Mathematics 10 (Pearson)
First, read only part a) of “Example 1: Using a Diagram to Model a Situation” on page 397.
Next, read only part a) of “Example 2: Using a Table to Create a Linear System to Model a Situation” on page 398.
Finally, read only part a) of “Example 3: Using a Linear System to Solve a Problem” on page 434.
 Try This 10
Try This 10
Write a system of equations to model the following scenario. As you answer TT10, consider the helpful questions/suggestions below:
Jennifer takes 5.9 h to drive her car 600 km from Edmonton to Dawson Creek. For the first part of the trip, her speed was 75 km/h, and for the rest of the trip, her speed was 110 km/h. How long did she drive at each speed?
Define the variables.
- What is the question asking for? Is it speed, distance, or time?
- What are the two quantities that you are looking for?
- What variables will you use to represent the two quantities?
Organize the information.
- How could you use a table similar to the following to organize your information?
|
|
Speed |
Time |
Distance |
|
First Part of Trip |
|
|
|
|
Second Part of Trip |
|
|
|
Write the equations.
- This question involves units of distance, time, and speed. What is the relationship amongst these three variables? (You may want to perform an Internet search using the keywords “distance time speed formula.”)
- What is the equation that would represent the total driving time?
- How could you use the formula to write the equation that would represent the total distance driven?
Possible TT10 Solutions
 Self-Check
Self-Check
Complete the following questions to check your understanding of the concepts covered in this lesson so far. Feel free to refer to the previous examples that you have previously encountered. In each case, create a linear system that could be used to model the situation described.
SC 1. The admission fee for the chuckwagon races at the Grande Prairie Stompede is $10.00 for children and $16.00 for adults. On a certain day, 2200 people entered the fair and $30 544 was collected. Determine the number of children and the number of adults that attended on this day.
SC 2. An exam worth 125 points contains 40 questions. Some of the questions are worth two points and some are worth five points. Determine the number of two-point questions and the number of five-point questions.
SC 3. Dominick invested $2000—one part at 6% per year and the other part at 8% per year. At the end of one year, he earned $133. Determine how much Dominick invested at each rate.
 Try This 11
Try This 11
Complete the following in your course folder ( binder).
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 11. Complete “Exercises” questions 6, 7, 9, and 12 on pages 401 and 402.
Use the link below to check your answers to Try This 11.
Possible TT1 Solutions
In this lesson you have encountered a variety of problems that can be modelled by a system of equations. These problems can be classified according to type. Some are related to money and investments, and others may deal with perimeter or mixtures and concentrations. You may have a different strategy for modelling one type of problem as opposed to another.
Module 7: Systems of Linear Equations
Connect
![]() Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Quizzes link to the left in moodle or under the Assess tab and ensure your work in your binder (course folder) is complete.
**Project NOT ASSIGNED**

© pressmaster/21747793/Fotolia
 Project Connection
Project Connection
In Lesson 1 you were asked to imagine that you and a group of friends had decided to take a trip. You are now ready to book your flights and accommodations. You will also want to make decisions regarding the transportation that you will need while you are vacationing.
At this time, go to the Unit 4 Project and complete the Module 7: Lesson 2 component of the project.
 Going Beyond
Going Beyond
If you go on to study mathematics, science, or engineering after high school, you may be required to take a course in linear algebra. Among other things, linear algebra teaches you different techniques for solving systems of equations. In this section you will search for a specialized online calculator that can be used to solve a system of equations. This calculator is programmed according to principles found in linear algebra.
A matrix is a rectangular array of numbers. Examples of matrices are as follows:
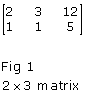
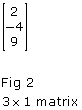

You can represent a system of equations as a matrix.
The system ![]() can be represented by the matrix
can be represented by the matrix ![]() .
.
Notice that only the coefficients of each term in the system are written in the matrix. Work through the following steps to solve this system of equations using an online matrix calculator.
- Use an Internet search engine to find an online matrix calculator. You may want to use search terms such as “matrix calculator” or “calculator rref.” Most of these online applets are easy to use—all you need to do is enter the matrix representing the linear system according to the instructions and then select “Solve” to see the answer.
- Once you have found an appropriate applet, input the matrix. Pay attention to the instructions. Some applets require spaces between numbers, and others may require commas or tabs.
- Select “Solve” or “rref.” Your answer will also appear as a matrix. Record this matrix, and explain what it means. According to the matrix, what is the solution to the linear system? Save your response in your course folder.
Many graphing calculators have a matrix feature. Check your calculator manual or go online to see how you can access this command and use it to check your answers to the questions you have and will encounter in this module. You can also check with your teacher, who may be aware of how to use this feature on particular graphing calculator models.
Module 7: Systems of Linear Equations
Lesson 2 Summary
In this lesson you investigated the following questions:
- How do you decide what parts of a problem should be represented by variables?
- How do you organize the information you need to create a linear system?
In this lesson you examined situations that could be modelled by a system of linear equations. You learned how to write linear systems that can be used to solve problems. One of the initial steps in modelling situations is to define the variables or the unknown quantities. In order to know how to define the variables, you must know what type of solution the problem demands. For example, if the problem asks for the number of quarters and the number of dimes, then the variables could be defined as follows:
q = the number of quarters
d = the number of dimes
The example also shows that you can avoid confusion by defining variables using letters that have meaning in the context of the problem.
In this lesson you organized and evaluated information about given situations and then created linear systems based on your work. You used diagrams to develop meaning and to get a sense of the situation. You also used tables to sort the data. By sketching diagrams and analyzing tables, you were able to develop appropriate linear systems.
Some of the problems in this lesson were solved by graphing. Many of the other problems that you modelled in this lesson were left unsolved. In the final lesson of this module, you will revisit these problems. At that time, you will employ various strategies to determine the solutions to these problems.

