Lesson 4: Solving Linear Systems by Elimination
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 4: Solving Linear Systems by Elimination |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 5:25 AM |
Module 7: Systems of Linear Equations
Lesson 4: Solving Linear Systems by Elimination
Focus

David Sacks/Lifesize/Thinkstock
Shopping can be a fun way to spend leisure time. It does not have to be an expensive endeavour. You can set a budget, or you can just go window shopping with some friends.
When the weather gets warmer, you can take your shopping outdoors and find some good bargains at garage sales or yard sales in your community. Perhaps you will uncover a missing piece to add to your special collection or an outfit that complements your current wardrobe.
Instead of shopping, you may discover multiple benefits if you decide to sell gently used items. First, you are eliminating unwanted items from your home. Second, you are doing your part for the environment by giving someone else the opportunity to reuse these products. Third, you can use the proceeds of the sale toward your own recreational pursuits.
In the last lesson you learned how to solve a linear system by using the substitution method. In this lesson you will learn a second algebraic technique for solving linear systems. This technique, called elimination, will depend on your ability to find or create matches from the equations in a system. Many of the math problems that you will encounter in this lesson are concerned with buying and selling items as a hobby.
Outcomes
At the end of this lesson, you will be able to
- determine the solution of a system of linear equations by using the elimination method
- verify the solution of a system of linear equations algebraically
Lesson Questions
- In using the elimination method, how do you know whether equations need to be multiplied, added, or subtracted?
- How does adding or subtracting the equations of a linear system affect the solution to the system?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Activities block on the left in moodle or under the Assess tab.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 7: Systems of Linear Equations
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your binder. If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
Answers
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources either before or after you try the questions in Are You Ready? Your teacher may also direct you to this section to review specific concepts.
In solving systems of equations algebraically, one key step may be the collection of like terms in an expression.
Read Collecting Like Terms to remind you of this technique.
-------------------------------------------
 Read
Read
One way to solve a system of linear equations is by substitution. For a review about how to use the method of substitution, it may be helpful to reread the following example from your textbook.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Solving a Linear System by Substitution” on pages 418 and 419.
Module 7: Systems of Linear Equations
Discover
You are familiar with adding and subtracting numbers and polynomials. In this lesson you will investigate the addition and subtraction of equations. Can equations be added or subtracted? What would be the benefit of doing so?
In this activity you will explore properties of linear systems, which will ultimately lead to a new strategy for solving a system of linear equations.
 Math Lab: Properties of Linear Systems
Math Lab: Properties of Linear Systems
Go Math Lab: Properties of Linear Systems and complete it.
Math Lab: Properties of Linear Systems
Once you have completed these questions, use the link below to check your answers. Make any corrections or notes as needed. File this in your binder.
Math Lab Answers
As you proceed in this lesson, think about how your discovery about the properties of equations can help you to solve a linear system algebraically.
Module 7: Systems of Linear Equations
Explore

© Patricia Hofmeester/3529689/Fotolia
Study the photo with various shoes scattered on the ground. How many pairs of shoes can you find? Have you ever experienced the frustration of not being able to find a missing shoe or a missing sock?
There are many examples of occasions when you need to find a pair. In terms of clothing, you may need to find matching pairs of socks, mitts, shoes, earrings, or knee pads. You may also want to find a matching top and bottom to wear.
You need to find matching pairs in games such as Memory and Go Fish. After you’ve found a match, you can remove the cards from the playing area and they are no longer a part of the game.
In this lesson you will learn another algebraic method for solving a system of equations. The basis for this method is to match like terms and eliminate them by adding or subtracting the equations in the linear system. You may have to manipulate the equations before you can find the match.
Glossary Terms
Add these terms and their definitions to the Glossary Terms section in your notes. You may also want to add examples that demonstrate how each term is applied.
- additive inverses
- elimination method
------------------------------------------------------
In Math Lab: Properties of Linear Systems, you observed that the graph of a linear equation formed by adding or subtracting the equations of a linear system also passes through the point of intersection. You also noticed that by adding or subtracting equations, you may end up with a result where a variable has been “eliminated.”
You may still have questions about these observations and how they can be used to solve linear systems. In fact, the practice of adding, subtracting, and even multiplying equations is a practice that is fundamental to the algebraic method of solving a linear system by a method known as elimination. Try the next exercise to see how the elimination method works.
 Try This 1 - 3
Try This 1 - 3
Complete the following in your course folder ( binder).
Try This 1 - 3 Questions
Use the link below to check your answers to Try This 1 - 3.
Possible TT1-3 Solutions
 Self-Check
Self-Check
Solve the following linear systems by applying the elimination method.
SC 1.
x − 3y = 1
2x + 3y = 26
SC 2.
5x + 4y = 20
3x + 4y = 24
------------------------------------
In the linear systems that you have worked with, you have been able to eliminate a variable by adding or subtracting the given equations in the system. Sometimes it is not possible to eliminate a variable just by adding and subtracting. You may need to manipulate the equations in some way in preparation for elimination.
Try the next activity with a partner ( if possible) to see how you can do this. Recall from your results in Math Lab: Properties of Linear Systems that multiplying each term in a linear equation by a constant does not change the solution of the linear system. With this in mind, work with a partner to solve the systems of linear equations in the following activity.
 Share 1 - 3
Share 1 - 3
Print the questions out and complete them with another classmate or appropriate partner ( if possible).
Share 1 - 3 Questions
Use the link below to check your answers to Share 1 - 3.
Possible S1-3 Solutions
-----------------------------------
Work through the next example to see a couple of ways that you can solve a system of linear equations by elimination.
Example
Consider the following linear system:
6a − 5b = 14
4a + 3b = 22
- Solve the linear system by using the method of elimination.
- Verify the solution.
Solution
- In this case, it is not possible to eliminate a variable by adding or subtracting the equations as they are. However, it is possible to eliminate either the a terms or the b-terms. Note: In the method of elimination, you are only looking for a way to eliminate one of the variables, not both!
Method 1: Eliminate the a-Term
To eliminate the a-term, you must multiply each equation by a constant so that the coefficients of the a-terms are either equal or additive inverses of each other. One way to determine this constant is to first determine the lowest common denominator of the current coefficients. Then multiply each equation by the factor that would result in a new coefficient equal to the lowest common multiple.
In this case, the lowest common multiple of 6 and 4 is 12. Since 2 × 6 = 12, and 3 × 4 = 12, the first equation should be multiplied by 2 and the second equation multiplied by 3.
2(6a − 5b) = 2(14)
3(4a + 3b) = 3(22)
12a − 10b = 28
12a + 9b = 66
To eliminate the a-terms, you must subtract the equations.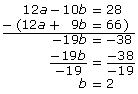
You can now determine the a-value by substituting b = 2 into one of the original equations.
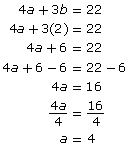
Method 2: Eliminate the b-Term
To eliminate the b-term, you must multiply each equation by a constant so that the coefficients of the b-terms are either equal or additive inverses of each other. You can find this constant by following the procedure in Method 1, where you first determine the lowest common multiple, or you could simply multiply each equation by the coefficient of the other equation.
In this case, you can multiply the first equation by 3 and the second equation by −5.3(6a − 5b) = 3(14)
−5(4a + 3b) = −5(22)
18a − 15b = 42
−20a − 15b = −110
To eliminate the b-terms, you must subtract the equations.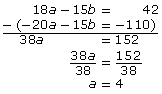
You can now determine the b-value by substituting b = 2 into one of the original equations.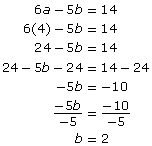
-
To verify the solution, substitute the a-value and b-value into the original equations.
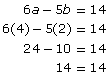
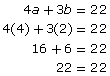
Since both equations are true, the solution is verified.
![]() Share 4 - 7
Share 4 - 7
Discuss the following questions with a partner ( if possible). Note down your answers in your course folder.
4. a. In both Method 1 and Method 2, substitution was avoided when determining one of the values. How can you avoid using substitution?
b. In what cases would it be better to not use substitution?
5. In both Method 1 and Method 2, the elimination method was based on subtracting the equations. How could you use addition to solve the system?
6. In what cases would you want to find the lowest common multiple of the two coefficients whose terms you are trying to eliminate?
7. In what steps in the solution do you think a student might commit an error?
Possible S4 - 7 Solutions
Module 7: Systems of Linear Equations
![]() Read
Read
- How do you prepare a linear system for elimination by addition?
- How is this different from preparing for elimination by subtraction?
| Foundations and Pre-calculus Mathematics 10 (Pearson) Read “Example 2: Solving a Linear System by Adding to Eliminate a Variable” on pages 432 and 433. |
![]() Watch and Listen
Watch and Listen

![]() Try This 4
Try This 4
Complete the following in your binder.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 4. Complete “Exercises” questions 3, 6, and 12 on pages 437 and 438.
Use the link below to check your answers to Try This 4.
Possible TT4 Solutions
You can use the elimination method to solve problems modelled by systems of linear equations. Go to your textbook to see how a problem is modelled and then solved by elimination. As you read, pay attention to the following:
->How is the information from the problem organized?
->How are the equations of the model prepared for the elimination of a variable?
|
Read “Example 3: Using a Linear System to Solve a Problem” on page 434. |
 Try This 5
Try This 5
Study each of the following problems. In Lesson 3 you chose one of the problems to model with a linear system. You will now use a system of equations to model the other problem. If you chose Problem 1 in Lesson 3, choose Problem 2 to answer TT 5 and vice-versa.
TT 5. Define the variables and solve the system using the method of elimination. Include any tables or diagrams that you may have used to help with the setup of the system.
Problem 1: The admission fee for the chuck wagon races at the Grande Prairie Stampede is $10.00 for children and $16.00 for adults. On a certain day, 2200 people enter the fair and $30 544 is collected. Determine the number of children and the number of adults that attended on this day.
OR
Problem 2: An exam worth 125 points contains 40 questions. Some of the questions are worth two points and some are worth five points. Determine the number of two-point questions and the number of five-point questions.
Possible TT5 Solutions
Mathematics 10C Learn EveryWare © 2010 Alberta Education
Module 7: Systems of Linear Equations
Connect
 Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Quizzes link to the left in moodle or under the Assess tab and ensure your work in your binder (course folder) is complete.
Update your Strategies for Solving Linear Systems page at this time as well.
 Project Connection **NOT ASSIGNED**
Project Connection **NOT ASSIGNED**

Digital/Vision/Photodisc/Thinkstock
Throughout the Unit 4 Project, you have been asked questions related to taking a vacation. Now imagine that you are taking your vacation. During a break in your itinerary, you decide to go shopping at the local outlet mall where brand-name stores sell last season’s fashions at discounted prices. At a particular shoe store, there is a sale where you can buy one pair and get the second pair for half price. In cases where the two pairs are of unequal value, the discount applies to the less expensive pair. For example, if one pair was $100 and the second pair was $60, then you would only receive the 50% discount on the $60 pair.
Now go to the Unit 4 Project, and complete the Module 7: Lesson 4 component of the project.
 Going Beyond
Going Beyond
You have previously considered the solution to a system of three equations in three variables. In this lesson you learned how to solve a linear system by elimination. You can solve a system of three equations in three variables by using the same method. In the Going Beyond section in Lesson 1, you explored how you might graph each equation in the following system.
x + y + z = 6
2x − y + z = 3
x + y − z = 0
- You can now use elimination to solve this same system of equations. Follow the steps below to find the values of x, y, and z that will satisfy the system.
- Choose two of the three equations. Use the elimination method to eliminate one of the variables. Call the resulting expression Equation A.
- Now choose a different pair of the original equations. One of the equations will be the same as in the first pair. Use the elimination method to eliminate the same variable as in step 2. Call the resulting expression Equation B.
- You should now have two equations with two variables. Solve the linear system represented by Equation A and Equation B.
- Use the values of the variables found in step 2 to determine the value of the third variable.
- How many other ways could you have solved this question using elimination?
- How can you verify your solution?
- How would you verify your solution with the online matrix calculator?
Save your work in your course folder.
Module 7: Systems of Linear Equations
Lesson 4 Summary
In this lesson you investigated the following questions:-
In using the elimination method, how do you know whether equations need to be multiplied, added, or subtracted?
-
How does adding or subtracting the equations of a linear system affect the solution to the system?
In this lesson you learned how to use the elimination method to solve systems of linear equations. This method is based on the properties of linear systems. The first property is that the solution to a linear system is unchanged when the equations in the system are either added or subtracted. The second property is that the solution is also unchanged when any equation in the system is multiplied by a constant. You discovered these properties when you graphed the sum, difference, and multiples of the linear equations. In doing so, you saw that the graphs passed through the same point of intersection as the original equations in the system.
To use the elimination method successfully, you learned that you have to match the coefficients of either the x-term or the y-term. You can do this by multiplying one or both equations by a constant. Once the coefficients match, you can either add or subtract the two equations in order to eliminate the term. If the matching coefficients have opposite signs, you would add the equations. However, if the matching coefficients have the same signs, then you would subtract the equations. The result is a simplified equation that can be solved for the remaining variable.
Did you know that a linear system can have different numbers of solutions? In the next lesson you will investigate the number of solutions of a linear system. In the last lesson of this module you will use the elimination method as a strategy in solving context-based problems. You will also make decisions about which solution strategy is the most appropriate in specific situations.