Lesson 5: Number of Solutions of a Linear System
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 5: Number of Solutions of a Linear System |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 5:22 AM |
Description
Created by IMSreader
Module 7: Systems of Linear Equations
Lesson 5: Number of Solutions of a Linear System
Focus

© Gino Santa Maria/11945614/Fotolia
Have you ever watched an ensemble dance performance? Perhaps you’ve attended a musical production or tuned in to a television program featuring competitive dancing. If you have, then you might have been impressed with the way that the dancers’ movements were synchronized, both with the music and with each other. The art of designing sequences of movement to form a dance is called choreography.
In addition to dance, choreography is used in other contexts that involve movement. Moves and routines are developed or choreographed in activities such as cheer leading, gymnastics, figure skating, fashion shows, and combat scenes, including sword fights in stage productions. In cheer leading, for example, you may also see pyramid formations. In ensemble choreography, you will often see different formations of the performers, including straight lines, rows, crosses, and staggered V-formations.
In this lesson you will investigate the formations of two lines. From Lesson 1 you are already familiar with the fact that two lines can intersect at a single point. In this lesson you will study the relative orientations of two lines on a coordinate plane and determine the implications for the number of solutions of such linear systems.
Outcome
At the end of this lesson, you will be able to explain, using examples, why a system of equations may have no solution, one solution, or an infinite number of solutions.
Lesson Questions
- Why can linear systems have different numbers of solutions?
- How do the equations of a linear system indicate the number of solutions of that system?
 Lesson Assessment and Completion
Lesson Assessment and Completion
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Activities block on the left in moodle or under the Assess tab.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 7: Systems of Linear Equations
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your binder. If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
Answers
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources either before or after you try the questions in Are You Ready? Your teacher may also direct you to this section to review specific concepts.
 Read
Read
A system of linear equations can be solved algebraically by substitution or elimination. For these algebraic solutions, review the following from examples from your textbook.
Foundations and Pre-calculus Mathematics 10 (Pearson)
If necessary, reread “Example 1: Solving a Linear System by Substitution” on pages 418 and 419.
You may also find it helpful to reread “Example 1: Solving a Linear System by Subtracting to Eliminate a Variable” on pages 430 and 431.
There are two more examples on the following pages if you wish to study them.
For a review of parallel lines, go to “Parallel” at LearnAlberta’s Mathematics Glossary.
There is a demonstration applet at the website that you can try. (HINT- See what happens when you put one line directly
on top of the other).
-------------------------------
Module 7: Systems of Linear Equations
Discover

© Robert L. BowlinJr./7610679/Fotolia
The Canadian Air Forces 431 Air Demonstration Squadron, commonly called the Snowbirds, is best known for outstanding air shows featuring pinpoint choreography and amazing stunts. If you have ever had a chance to watch the Snowbirds in action, you will know that a trademark at air shows is the ability of the pilots to guide their planes from one formation to another.
In this Discover activity you will examine the different formations of two lines on the coordinate plane.
 Try This 1 - 7
Try This 1 - 7
Complete the following.
Try This 1 - 7 Questions
Use the link below to check your answers to Try This 1 - 7.
Possible TT1-7 Solutions
Module 7: Systems of Linear Equations
Explore

Comstock/Thinkstock
If you like to dance, sing, or act, you may want to consider participating in community theatre in your leisure time. Community theatre provides opportunities for people to work together to put on stage productions from one-act plays to full-scale musical productions. There are many community theatres all across Alberta from the small towns to the big cities. Some famous actors even got their start in community theatre!
The director of a community theatre production has many duties, one of which is to hold auditions. At auditions, people interested in getting a role in the production showcase their acting skills privately in front of the director. Based on the auditions, the director can make decisions about how to cast the play. For a particular role, the director may find one ideal candidate, no candidates, or many candidates. If there are many candidates for a role, then the director may decide to offer the role to two people and have each person alternate performances, especially in the case of a long production run where the show is staged multiple times.
In this lesson you will analyze the graphs and equations of linear systems to determine the nature of the solutions. Just as in the case of a director, you may find instances when there is a single solution, no solution, or infinitely many solutions!
In Lesson 1 you investigated solving systems of linear equations by graphing. In that lesson, you only encountered situations where each system had a unique solution. In other words, there was only one point of intersection. The coordinates of this point represented the values of x and y that satisfied both equations in the system. It is also possible for two lines to intersect infinitely many times or to never intersect.
Glossary Terms
Add these terms and their definitions to the Glossary Terms section in your notes. You may also want to add examples that demonstrate how each term is applied.
- coincident lines
- consistent system
- dependent system
- inconsistent system
- independent system
---------------------------------------
 Watch and Listen
Watch and Listen
Go to the Math Dude and watch a video about "Solving systems of equations".
Watch the video from the 3:30 mark to the end. (This is the same video from Lesson 1 that you started watching to he 3:30 point). Are the graphs that are presented in the video the same as the ones you generated in TT 4? As you watch, see if you can find a way to recognize the number of points of intersection by analyzing the equations in the system prior to graphing. You may want to press pause to momentarily stop the video when the equations are displayed.
--------------------------------------------
In the Discover section you considered the different ways that two straight lines can intersect. You may have come up with the following three possibilities.
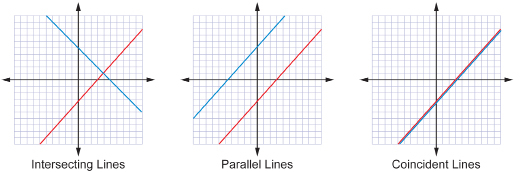
 Try This 8
Try This 8
Complete the following. You will complete a table that is related to the three graphs you have just studied.
Try This 8 Questions
Use the link below to check your answers to Try This 8.
Possible TT8 Solutions
You can always determine the number of intersection points and solutions of a linear system by graphing the equations in the system. Sometimes, however, this may be inefficient or impractical.
In the remainder of this lesson, you will develop methods for identifying the number of solutions in a linear system by analyzing both the properties of the equations in the system.
 Try This 9 - 12
Try This 9 - 12
Complete the following. You will again refer to the three graphs you have just studied. Work with a partner to complete TT 11 if possible.
Try This 9 - 12 Questions
Use the link below to check your answers to Try This 9 - 12.
Possible TT9 - 12 Solutions
 Read
Read
Go to your textbook to see how you can identify the number of solutions of a system by analyzing the slope and the y-intercepts of the linear equations. As you read, try to find out the answers to the following questions:
- Why is it unnecessary to check the y-intercepts of the equations if the slopes are identified as unequal?
- Why is it necessary to check the y-intercepts of the equations if the slopes are identified as equal?
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Determining the Number of Solutions of a Linear System” on pages 444 and 445.
Complete the following questions to check your understanding of the concepts covered in this lesson so far.
 Self-Check
Self-Check
Determine the slopes and y-intercepts of each system; then identify the number of solutions for the system. In your response, be sure to include reasons that support your answer.
SC 1.
y = x + 1
y = x - 2
SC 2.
2x + 3y = 12
4x + 6y = 24
SC 3.
7x - 4y = 8
7x + 4y = 8
So far, you have studied two methods of determining the number of solutions of a linear system:
- Method 1: You can graph the equations of the system and check the number of points of intersection.
- Method 2: You can compare the slopes and the y-intercepts of each equation in a system.
In the next part of the lesson, you will investigate a third method based on an inspection of the equations in the system when written in standard form. Recall that standard form is when the equation of a line is written in the form Ax + By = C.
 Share 1 - 2
Share 1 - 2
Complete the following.
Share 1 - 2 Questions
Use the link below to check your answers to Share 1 - 2.
Possible S1-2 Solutions
Module 7: Systems of Linear Equations
What happens if you try to algebraically solve a linear system that has either no solutions or an infinite number of solutions? What will your answer look like? To find out, complete the Try This questions below.
 Try This 13 - 16
Try This 13 - 16
Complete the following.
Try This 13 - 16 Questions
Use the link below to check your answers to Try This 13 - 16.
Possible TT13-16 Solutions
 Read
Read
Go to your textbook to solidify your understanding of how the number of solutions of a linear system relate to the terms of the equations in the system.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 2: Creating a Linear System with 0, 1, or Infinite Solutions” on page 446. As you read, focus on the differences between the methods used in parts a) and b) compared to part c).
 Self-Check
Self-Check
SC 4.
- In the system of linear equations y = 2x + 3 and y = 2x + b, what values of b will result in a system that has no solution?
- What values of b will result in a system that has one solution?
- What values of b will result in a system that has an infinite number of solutions?
SC 5.
- In the system of linear equations y = -3x + 4 and y = mx + 4, what values of m will result in a system that has no solution?
- What values of m will result in a system that has one solution?
- What values of m will result in a system that has an infinite number of solutions?
SC 6. How many solutions does each linear system have? Show how you know.
- 2x + 3y = 20
6x - y = 20 - x - 5y = 1
-x + 5y = 1 - x + 3y = 5
2x + 6y = 10
To help you with SC 7, retrieve your flow chart from Try This 12. You created it for identifying the number of solutions in a linear system. Think about the strategies that you used and that can be applied to this problem. Do the question; then return to the flow chart to evaluate its success in tackling this problem. Make any necessary revisions to the flow chart.
SC 7. Consider the following four linear equations.
|
Line |
Considerations |
|
A |
6x + 2y = 16 |
|
B |
9x + 3y = 12 |
|
C |
-3x + y = 8 |
|
D |
6x - 2y = -16 |
- Identify two lines that form a system that has no solution.
- Identify two lines that form a system that has one solution.
- Identify two lines that form a system that has an infinite number of solutions.
 Try This 17
Try This 17
For some final practice, complete the following in your binder.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 17. Complete “Exercises” questions 4, 5, 6, 7, 10, 11, and 12 on page 448.
Use the link below to check your answers to Try This 17.
Possible TT17 Solutions
---------------------------------
![]()
Now it's time to have some fun playing a game to practice all of the skills you have learned about Linear Systems.
Use the link below to play the Flying Acrobats game.
---------------------------------
Module 7: Systems of Linear Equations
Connect
In this lesson you have discovered that a linear system can have a number of different solutions or no solutions at all. You created a flow chart that helps you to identify the number of solutions of a system based on its equations. As you undertake the tasks in this section, refer to your flow chart often to support your work.
 Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Quizzes link to the left in moodle or under the Assess tab and ensure your work in your binder (course folder) is complete.
 Project Connection **NOT ASSIGNED**
Project Connection **NOT ASSIGNED**

© Pedro Nogueira/
1893623/Fotolia
Depending on where you are vacationing, you may have opportunities to attend a live performance. You could attend a dramatic production, a live concert, a magic show, or a standup comedy performance. As part of your final module project, you will put your own abilities to the test by creating a performance piece about the concepts that you have learned in this module.
Go to the Unit 4 Project, and complete the Module 7: Lesson 5 component of the project.
 Going Beyond
Going Beyond
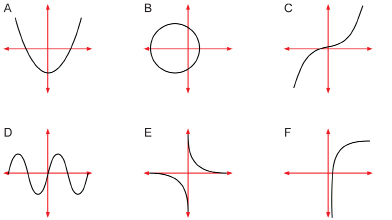
How can a system of equations contain exactly two solutions?
A system of linear equations cannot have exactly two solutions, since two lines cannot intersect exactly twice. However, in the case of non-linear systems, where at least one equation in the system is not represented by a straight line, then it is possible to have exactly two solutions.
Part A
The illustration above shows some non-linear graphs that you may encounter in future math courses.
- For each of the graphs shown in the illustration, state all possible solutions for a system of equations comprised of a linear equation and an equation represented by the graph. In other words, determine how many different ways a straight line can intersect each of the graphs above.
You may want to print out a copy of these graphs and then use a ruler, pencil, or other straightedge to see how many ways a straight line can intersect each graph. For example, a straight line can intersect Graph A once, twice, or not at all. Therefore, the system could have one solution, two solutions, or no solutions.
Part B
How would you solve a non-linear system algebraically?
- See if you can use a method that you have learned in this module to solve the following non-linear systems.
- y = -3
y = x2 - 3 - x - y = 2
(x + 2)2 + y2 = 16
- y = -3
Save your responses in your course folder. Your teacher may choose to examine your work at a later time.
Module 7: Systems of Linear Equations
Lesson 5 Summary
In this lesson you investigated the following questions:
- Why can linear systems have different numbers of solutions?
- How do the equations of a linear system indicate the number of solutions of that system?
Up until this lesson, you focused on systems that had only one solution or those systems whose graphs contained only one point of intersection. In this lesson you learned that a system of linear equations with two variables can also have no solutions or an infinite number of solutions. You discovered this by graphing each of the different ways that two lines can be oriented relative to each other on a coordinate plane. If two lines are parallel, then they will have no solutions because there will not be a point of intersection. On the other hand, if two lines are coincident, then they will have an infinitely many points of intersection and, therefore, infinitely many solutions.
Besides analyzing graphs, you also analyzed the equations of systems for clues about the number of solutions for the systems. You discovered that, by determining the slopes and the y-intercepts of each equation in the system, you could identify the number of solutions. If the equations have a common slope as well as a common y-intercept, then the system has an infinite number of solutions. A system whose equations have only a common slope, but differing y-intercepts will have no solution since the lines will be parallel. Finally, a system whose equations do not share the same slope will have only one solution.
Another way of identifying the number of solutions of a linear system is by analyzing the coefficients of each equation in standard form. For example, if one equation is a multiple of the other equation, then there are infinitely many solutions. If the left side of one equation is not a multiple of the left side of the other equation, then there is only one solution. All other cases represent those systems with no solutions.
In the final lesson of this module, you will work with others to solve problems modelled by systems of linear equations. You will revisit all of the strategies that you have learned to solve linear systems. You will practise modelling systems and solving them based on the selection of the most appropriate strategy for each problem.


