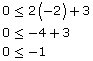Lesson 6: Solving Problems with Linear Systems
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 6: Solving Problems with Linear Systems |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 5:23 AM |
Module 7: Systems of Linear Equations
Lesson 6: Solving Problems with Linear Systems
Focus

© Bobo Ling/1445396/Fotolia
Origami is the Japanese art of paper folding. With origami, you can create shapes that represent animals, flowers, toys, and other 3-D objects. The types of creations range from the simple to the complex. Origami is a recreational activity that stimulates creativity and improves manual dexterity, the ability to use hands with ease.
Origami has long been a subject of interest amongst mathematicians. Some studies have focused on whether certain models can be flattened without causing damage to them. Other studies have based the solution to mathematical equations on the creases of origami models.
Computer applications have been designed to assist in the design of origami models. Starting with a very basic drawing of an animal, for example, measurements would be taken that described the position of the animal’s parts. Then a system of equations based on those measurements would be developed. There could be a linear system comprised of hundreds of equations. The computer application then computes the solution to the system, which results in a crease pattern for the construction of the animal.
In this lesson you will apply the techniques that you have learned in this module to problems that require systems of equations to solve. You will encounter problems that are familiar and others that are novel. You will use these problems to test and refine your own personal strategies. The final lesson of this module will focus on hobbies that require manual dexterity.
Outcomes
At the end of this lesson, you will be able to
- explain a strategy to solve a system of linear equations
- solve a problem that involves a system of linear equations
Lesson Questions
- Why is it necessary to learn several methods for solving a problem?
- How can you recognize which strategy is most appropriate for solving a given system of equations?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Activities block on the left in moodle or under the Assess tab.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 7: Systems of Linear Equations
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your binder. If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
Answers
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources either before or after you try the questions in Are You Ready? Your teacher may also direct you to this section to review specific concepts.
 Read
Read
A system of linear equations can be solved algebraically by substitution or elimination. For a sample of these algebraic solutions, look at the following examples from your textbook.
Foundations and Pre-calculus Mathematics 10 (Pearson)
If necessary, reread “Example 1: Solving a Linear System by Substitution” on pages 418 and 419.
You may also find it helpful to reread “Example 1: Solving a Linear System by Subtracting to Eliminate a Variable” on pages 430 and 431.
You will find more examples on the following pages if you would like to look at more.
How do the characteristics of systems of linear equations correspond to the number of solutions the system has? If you don’t remember, have a look at Self-Check 4 of Lesson 5 again.
--------------------------------
Module 7: Systems of Linear Equations
Discover
In this module you have learned multiple methods for solving linear systems both graphically and algebraically.
In the Discover section you will work with a partner (if possible)to analyze linear systems to determine the best approach to adopt when facing systems of particular types. As you work through this section and throughout this lesson, you may want to have handy your Strategies for Solving Linear Systems document that you saved to your course folder. Remember that you can add to your document as you construct new understanding.
 Share 1 - 5
Share 1 - 5
Complete the following in your binder. Work with a partner if possible.
Share 1 - 5 Questions
Use the link below to check your answers to Share 1 - 5.
Possible S1-5 Solutions
Mathematics 10C Learn EveryWare © 2010 Alberta Education
Module 7: Systems of Linear Equations
Explore

iStockphoto/Thinkstock
The Tower of Hanoi puzzle.
To solve the Tower of Hanoi puzzle, you must move all the disks from one peg to another according to certain rules. You may only move one disk at a time. Also, the move may only be made to an empty peg or on top of a larger disc on a non-empty peg. Applying a certain sequence of steps allows you to solve the puzzle in a minimum number of steps.
(You may want to use your Internet search engine with the keywords “Tower of Hanoi” to learn more about this puzzle and to play an online version.)
In some ways, solving systems of equations is similar to solving the Tower of Hanoi puzzle. You have learned three methods of solving linear systems. Each of these methods requires that a certain sequence of steps be applied. The more you practise using these steps, the better you will become at solving linear systems!
 Read
Read
Consider different strategies for solving a problem that can be modelled by a system of linear equations. Go to your textbook and work through an example that shows how you can solve a problem with either graphing technology or by algebraic methods. As you read, consider the advantages and disadvantages of each approach. Also, consider other strategies that might work. Why do they work here? Which method do you prefer?
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 2: Using a Linear System to Solve a Problem” on pages 420 and 421.
In Lesson 2 of this module, you modelled various situations with systems of linear equations. In this lesson you will revisit those problems and solve them using both the algebraic and graphical methods that you have learned.
 Try This 1 - 4
Try This 1 - 4
At the beginning of Lesson 2, you created a system of equations to model the following problem:
Andrea has a bag of coins. There are 32 coins altogether, consisting of quarters and dimes. The total value of the coins is $5.90. Determine the number of quarters and the number of dimes in the bag.
Complete the following in your binder.
TT 1. Define the variables in the problem. Recreate the linear system that models this problem. Go back to your previous work to check that you have the correct set-up.
TT 2. Analyze your system and choose an appropriate strategy—graphing or algebraic—for solving the system. Then solve the system.
TT 3. Verify your solution quantitatively and qualitatively by doing the following steps.
a. Check that the solution values comply with the conditions stated in the problem.
b. Substitute the solution values in the original equations of the linear system.
TT 4. Once you have solved the system, evaluate your method. Was it the most appropriate strategy? Provide reasons to support your answer.
Use the link below to check your answers to Try This 1 - 4.
Possible TT1-4 Solutions
---------------------------------
The following example features a problem that you previously encountered in Lesson 2.
Example
Jennifer takes 5.9 h to drive her car 600 km from Edmonton to Dawson Creek. For the first part of the trip, her speed was 75 km/h, and for the rest of the trip her speed was 110 km/h.
- How long did she drive at each speed?
- How far did she drive at each speed?
Go to your course folder and retrieve your work related to this problem in Lesson 2 and do the following:
- Study how the linear system is established. Compare that with your own approach. Be sure that your approach leads to the same linear system.
- Solve the system using what you feel is the best method.
Then study the solution.
Solution
- Define the Variables
Let x = the time required to drive the first part of the trip.
Let y = the time required to drive the second part of the trip.
Organize the Information
Write the EquationsSpeed
Time
Distance
First Part of Trip
75
x
Second Part of Trip
110
y
The formula relating speed, time, and distance is d = st.
The equations of the linear system areSpeed
Time
Distance
First Part of Trip
75
x
75x
Second Part of Trip
110
y
110y
Total
x + y
75x + 110y
• total driving time: x + y = 5.9
• total distance driven: 75x + 110y = 600
Solve the Linear System
You can use substitution to solve this problem.
Rearrange the first equation.
y = 5.9 – x
Substitute the expression for y into the second equation.
75x + 110 (5.9 – x) = 600
Expand and solve for x.
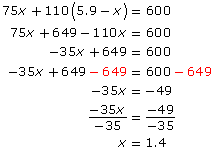
Substitute x = 1.4 into the equation y = 5.9 – x
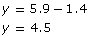
Jennifer drove for 1.4 h at 75 km/h; then she drove for 4.5 h at 110 km/h.
Verify the Solution
Check that the solution satisfies both equations in the linear system.
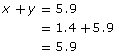
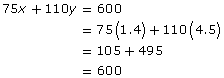
This solution also conforms to the conditions of the problem. The total time is 1.4 + 4.5 = 5.9 h. The total distance driven is 600 km. - Once you know the values of x and y, you can also determine how far Jennifer drove at each speed.
Refer to the chart used to organize the information. Use the expressions for distance to determine the length of each part of the trip.
First part of the trip:
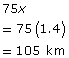 Second part of trip:
Second part of trip:
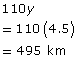
How is the solution strategy different from what you used to solve the problem?
 Share 6
Share 6
Complete the following.
Share 6 Questions.
Use the link below to check your answers to Share 6.
Possible S6 Solutions
----------------------------------
 Watch and Listen
Watch and Listen
Go to the site Writing Systems for some advice on how to set up the equations from word problems and to see a solved example.
----------------------------------
 Self-Check
Self-Check
For each of the following questions, do the following:
- Write a system of linear equations to model the situation.
- Choose a strategy and use it to solve the problem.
- Verify your solution; then evaluate the strategy that was used.
The key is figuring out whether to use the graph, substitution, or elimination strategy and deciding why one strategy may be better than the others.
SC 1. Two numbers have a sum of 60. Their difference is 6. Determine the two numbers.
SC 2. The mass of two bags of fertilizer differed by 10 kg. The larger bag contained 30% nitrogen. The smaller bag contained 20% nitrogen. The total mass of nitrogen in both bags was 16 kg. What was the mass of each bag?
 Try This 5
Try This 5
Complete the following in your binder.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 5. a. Complete “Review” question 13 on page 453.
b. Complete “Practice Test” questions 5.a) and 6 on page 455.
c. Complete “Cumulative Review” question 28 on page 461.
Use the link below to check your answers to Try This 5.
Possible TT5 Solutions
Module 7: Systems of Linear Equations
Connect
 Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Quizzes link to the left in moodle or under the Assess tab and ensure your work in your binder (course folder) is complete.
 Project Connection **NOT ASSIGNED**
Project Connection **NOT ASSIGNED**

iStockphoto/Thinkstock
You will now have an opportunity to return to the other Project Connections in this module to complete what you have previously started.
Go to the Unit 4 Project, and complete the Module 7: Lesson 6 component.
.
 Going Beyond
Going Beyond
Throughout this module, you have modelled and solved systems of linear equations. Some problems can be modelled by solving a system of linear inequalities.
Part A
Step 1: Use graph paper or the Graph Paper Template to graph the equation y = 2x + 3. The line that you graphed divides the coordinate plane into two half-planes.
Step 2: Go to the Pairs Table document. Choose any three points on one side of the line and record them as ordered pairs in the left-hand column in the table provided in the document. Make sure to save your Pairs Table document to your course folder.
Step 3: In the right-hand column of the table in the Pairs Table document, substitute the coordinates of each ordered pair into the expression. Simplify the expression and decide if the final expression is true or false. An example is shown below.
|
(x, y) |
|
|
(-2, 0) |
False, since 0 is greater than -1. |
Step 4: Repeat steps 2 and 3 for three points on the other side of the line, in the other half-plane. Remember to save your updated Pairs Table document to your course folder.
Step 5: You may have noticed that one half-plane contains points that yield true expressions, whereas the points in the other half-plane leads to false expressions. Shade in the half-plane that yields true expressions. This is the graph of the linear inequality ![]() since all of the points in the shaded region represent ordered pairs that satisfy the inequality.
since all of the points in the shaded region represent ordered pairs that satisfy the inequality.
Step 6: Follow a similar procedure to graph a second inequality ![]() on the same set of axes as the previous one. Start by graphing x + 2y = 4; then apply steps 2 to 4.
on the same set of axes as the previous one. Start by graphing x + 2y = 4; then apply steps 2 to 4.
Part B
With a partner, discuss the following questions and come up with some responses. You may search the Internet for related topics to supplement your discussion. Record your responses and save them in your course folder.
- a. Where do the graphs of the linear inequalities intersect?
b. How is this different from the intersection of two linear equations? - How many solutions are there for this system of linear inequalities?
- What real-life situation could be modelled by a linear inequality or a system of linear inequalities?
- Sketch a system of linear inequalities that has no solution. You do not need to write the system itself.
Save your responses in your course folder.
Module 7: Systems of Linear Equations
Lesson 6 Summary
In this lesson you investigated the following questions:
- Why is it necessary to learn several methods for solving a problem?
- How can you recognize which strategy is most appropriate for solving a given system of equations?
In the final lesson of this module you evaluated the strategies that you have learned for both modelling and solving linear systems. You revisited the problems that you previously modelled with linear systems in Lesson 2. You were able to confirm that the systems were properly set up. You also encountered a variety of other types of problems. You used what you learned previously about defining variables, organizing information, writing equations, and verifying solutions to solve the problems in this lesson.
In this lesson you worked with your peers to compare the strategies, determining both the benefits of drawbacks of each one. By having multiple strategies in your repertoire, you become more prepared to tackle a variety of problems. You may have discovered that some strategies work better with certain problem types, while other strategies are suited to other types of problems. By learning several solution strategies, you can choose one that enables you to solve the problem.
The benefit of the graphing method is that it can help you to visualize the solution. The graphing method is best suited to those systems whose equations are easily graphed. The drawback of this method is that it does not always provide an exact solution. You can improve the precision of the solution values by using graphing technology. However, unless the point of intersection occurs at a lattice point, you will be forced to estimate the solution. Sometimes it is difficult to know if graphing is going to provide a suitable solution until you have already graphed the system.
The algebraic methods that you learned in this module, including substitution and elimination, can provide exact solutions. The method of substitution is suited for questions where a variable is already isolated or can easily be isolated. On the other hand, the method of elimination can be employed in all other situations, particularly those situations where the coefficients of the like terms in each equation match.
Ultimately, the strategy that you choose to solve a problem is based on personal preference. It is important, however, to learn several ways of approaching a problem as you continue your math studies. This will prepare you for a greater array of problem-solving demands and give you the confidence to tackle them efficiently.