Lesson 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-1 SS |
| Book: | Lesson 1 |
| Printed by: | Guest user |
| Date: | Thursday, 4 December 2025, 2:08 AM |
Description
Created by IMSreader
1. Lesson 1
Module 1: Sequences and Series
Lesson 1: Arithmetic Sequences
Focus

Brand X Pictures/Thinkstock
Are you saving money? Do you have a savings account or do you keep your coins in a safe place at home? Perhaps you want to attend college or university in the future. You may want to visit a foreign country after you graduate, or you may want to invest in a nice car. Whether you want to save for your education or finance an automobile, saving money is easy to do and can help you reach your goals.
There are many ways to save money. One of the easiest ways to save is to put aside a portion of your allowance or earnings from a part-time job. How much you put aside depends on how quickly you want to reach your goals. Some people like to put aside a set amount, like $50 each month. If you followed this practice of saving, can you figure out how much you will have saved at the end of two years?
In this lesson you will learn about arithmetic sequences. If you deposited $50 in your bank account every month, the monthly balances would form an arithmetic sequence. You will develop and learn strategies to figure out your balance at any point in the future. Doing so allows you to design a savings plan that will help you meet your financial goals.
Outcomes
At the end of this lesson you will be able to
- identify any assumptions made when defining an arithmetic sequence
- provide and describe an example of an arithmetic sequence
- determine a rule for finding the general term of an arithmetic sequence
- determine t1, d, n, or tn in a problem that involves an arithmetic sequence
Lesson Questions
In this lesson you will investigate the following questions:
- How can you find any term in an arithmetic sequence?
- How are patterns important in the real world?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 1 Assignment (Download the Lesson 1 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Module 1 Glossary Terms and Formula Sheet
- work under Project Connection
Self-Check activities are for your own use. You can compare your answers to suggested answers to see if you are on track. If you are having difficulty with concepts or calculations, contact your teacher.
Materials and Equipment
You will need a calculator.
Time
Each lesson in Mathematics 20-1 Learn EveryWare is designed to be completed in approximately two hours. You may find that you require more or less time to complete individual lessons. It is important that you progress at your own pace, based on your individual learning requirements.
This time estimation does not include time required to complete Going Beyond activities or the Module 1 Project.
1.1. Launch
Module 1: Sequences and Series
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? This section, which includes Are You Ready? and Refresher, will help you find out.
Before beginning this lesson you should be able to
- define and provide examples of natural numbers
- identify and apply patterns when given a table of values
- rearrange and evaluate formulas
1.2. Are You Ready?
Module 1: Sequences and Series
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Determine the pattern in each table and apply the pattern to complete the table.
- Rearrange the following formulas for the indicated variable.
- Determine the value for each of the formulas below by substituting the given variables.
Formula
Variables
a.
V =
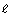 wh
wh 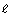 = 10 cm
= 10 cmw = 7 cm
h = 3 cm
b.
vf = vi + at
vi = 20.34
a = 9.81
t = 5.22
c.
A = 2πr2 + 2πrh
r = 4.5 in
h = 5.0 in
Answer
How did the questions go? If you feel comfortable with the concepts covered in the questions, skip forward to Discover. If you experienced difficulties, use the resources in Refresher to review these important concepts before continuing through the lesson.
1.3. Refresher
Module 1: Sequences and Series
Refresher
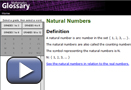
Visit Natural Numbers. Review the definition, and then follow the link to the demonstration applet. The demonstration applet shows how the number sets in the real number system are related to one another.
Move your cursor over the applet to see examples of natural numbers and examples from other number sets. Can you think of a few examples for each number set that are different than those shown in the applet?
You may need to ask your teacher for your school’s LearnAlberta login information.
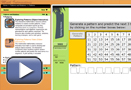
Use Extending Patterns Applet to review patterns in a table of values and pattern extension by applying the pattern rule. Try to discover how you can find patterns by comparing numbers up and down the same column and by comparing numbers across the same row.
Now watch Exploring Patterns Video. Click on the tap-dancing image or the video link to watch an application of patterns in tap dancing!
Try your hand at identifying and completing patterns by playing Exploring Patterns Video Interactive.
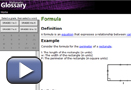
Visit Formula for a definition and to review rearranging formulas. Under “Example” you will see how the width variable in the perimeter formula can be isolated by balancing both sides of the formula. There is a second example that shows how the radius variable in the circumference formula can be isolated.
Isolating variables is an important skill. This skill will save you a lot of time. You won’t need to guess and check, and you will have a method that lets you find the answer for any variable when given a formula.
Go back to the Are You Ready? questions and try them again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 1: Sequences and Series
Discover
Try This 1

Digital Vision/Thinktock
Study the arrangement of marbles in each figure, and then answer the questions. Remember to save your responses in your course folder—you will need those responses in the upcoming Share 1.
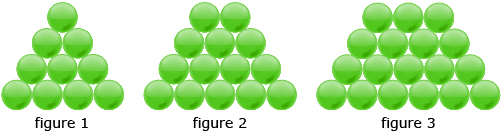
- If the pattern continues, how many marbles would each of the next two figures have? How did you determine your answer?
- Describe how you would find the number of marbles in figure 20. Use your method from question 1 to determine the number of marbles.
- Describe how you would find the number of marbles in figure 100. Use your method from question 1 or find a new method to determine the number of marbles.
- Was your method for determining the number of marbles in figure 20 different from your method used for figure 100? If yes, why did you choose a different method? If no, can you think of another method that might be more efficient? Explain.
![]() Save your work in your course folder.
Save your work in your course folder.
Share 1
If you do not have access to a discussion board, another student, or an appropriate partner with whom to share your work, talk to your teacher. For more information on Share discussions, refer to the Course Introduction or contact your teacher.
Share your responses from Try This 1 with a partner or group.
- Compare the answers for questions 1, 2, and 3. Are the answers given by your classmates similar to your own? Explain reasons for any differences.
- Compare and discuss your method for solving questions 2 and 3 with methods used by your classmates.
![]() If your teacher requires, you may need to place a summary of your Share discussion in your course folder.
If your teacher requires, you may need to place a summary of your Share discussion in your course folder.
You may have found that there really are a variety of ways to solve the problem. As you move through the lesson, you will encounter other strategies you can use when you revisit the Try This 1 problem later in the lesson.
1.5. Explore
Module 1: Sequences and Series
Explore
John Howard/Lifesize/Thinkstock
Some parents teach their children how to manage their money by giving them an allowance, or pocket money. The amount of the allowance may depend on the child’s age, his or her responsibilities, and other factors. Have you ever received an allowance? How did you spend your money?
Suppose a parent decides to give her son $5 per week, starting on his 6th birthday. Every year, he receives a “raise” in his allowance—an additional $3 per week. Can you determine what his allowance will be when he turns 17? By the end of this lesson you will be able to figure that out.
As you work through the lessons, you will come across math-related words that are unfamiliar to you. These words will be used over and over again, so it is important that you understand their meaning.
![]() Save Module 1 Glossary Terms in your course folder now.
Save Module 1 Glossary Terms in your course folder now.
Each time you come across a new term in Mathematics 20-1, add the term and a definition to your copy of Module 1 Glossary Terms.
Remember that this glossary is for you! While your teacher will want to know that you are keeping your glossary document updated, the contents of the document will ultimately benefit you as you learn and review the concepts presented in this course. It is important that you write down definitions in a way that makes sense to you. For example, if you don’t understand the dictionary's definition, look elsewhere for wording that makes sense to you.
Here are some of the words you will want to define in Module 1 Glossary Terms in this lesson:
- coefficient
- sequence
- term
- arithmetic sequence
- common difference
- general term
1.6. Explore 2
Module 1: Sequences and Series
Try This 2
Consider these examples of sequences.
A |
1, 8, 15, 22, 29, 36, ... |
B |
1, 2, 4, 8, 16, 32, ... |
C |
2, 4, 6, 8, 10, 12, 14, ... |
D |
2, 3, 5, 8, 12, 17, 23, ... |
E |
40, 35, 30, 25, 20, 15, ... |
Arithmetic has two different pronunciations depending on how you are using the term. For example, if you use arithmetic as a noun, it is pronounced a-RITH-me-tic. Young children learn reading, writing, and arithmetic (a-RITH-me-tic). When you use the term as an adjective, it is pronounced a-rith-MET-ic. In high school math, adolescents learn about arithmetic (a-rith-MET-ic) sequences.
- In your own words, describe what is meant by a sequence.
- Some of the sequences in the table are based on a similar pattern. Study the sequences. Can you identify which sequences have a similar pattern?
- How are the sequences that you selected similar? Describe the common pattern.
- Refer to the definition for arithmetic sequence that you added to Module 1 Glossary Terms. Determine which sequences in the examples given in the table are arithmetic sequences. Were these the same sequences you selected in question 2?
- Look through the six sequences again to make sure you didn’t miss any. Describe the properties of the other sequences that disqualify them as arithmetic sequences.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.7. Explore 3
Module 1: Sequences and Series
Arithmetic Sequences Increase by a Specific Factor

In Try This 2 you may have recognized that an arithmetic sequence increases by a specific factor. Example 1 in the image shows an arithmetic sequence that increases by a specific factor, 3, as you move between terms. An arithmetic sequence can also have terms that decrease by a factor (e.g., −5), as shown in example 2.
You will now explore methods used to find any term in a sequence. In the first method you will repeat many calculations on your calculator. In the second method you will apply a formula.
Finding a Term in an Arithmetic Sequence
Calculator Method
In Try This 1 you came up with a method to find the 20th number in the arithmetic sequence 10, 14, 18, ….
You may have started with the first term, and then used a calculator to repeatedly add the number 4, which is the common difference in this sequence.
Many calculators can simplify repeated calculations.
Follow these steps to find the 20th term of the sequence 10, 14, 18, ….
Step 1: Press ![]()
![]() , the first term in the sequence.
, the first term in the sequence.
Step 2: Press ![]() then
then ![]() then
then ![]() . The result will be the second term in the sequence.
. The result will be the second term in the sequence.
Step 3: While counting the terms, continue to press ![]() until you obtain the value of the 20th term. You do not need to press
until you obtain the value of the 20th term. You do not need to press ![]() then
then ![]() repeatedly.
repeatedly.
Try This 3

iStockphoto/Thinkstock
- Use the calculator method to find the 100th term in 10, 14, 18, ….
- What do you think are the advantages and disadvantages of evaluating repeated calculations with a calculator?
![]() Place a copy of your responses in your course folder.
Place a copy of your responses in your course folder.
1.8. Explore 4
Module 1: Sequences and Series
Algebraic Method
Even with a calculator, repeated calculations may not be very efficient, especially if you were asked to determine the value of a term that is far into the sequence. That’s where an algebraic method helps.
You can use an algebraic method to identify specific terms in an arithmetic sequence. In Try This 4 you will develop a formula for evaluating arithmetic sequences.
When working with arithmetic sequences, you will encounter and use terms that describe the sequence’s properties. These variables include the following:
Variable |
Meaning |
a |
the first term in the sequence (or t1) |
d |
the common difference |
n |
the position of the term in the sequence |
tn |
the value of the nth term |
You can use the variable tn to refer to any term in the sequence. Here are some examples:
- If you are solving for the third term in a sequence, simply replace the n in tn with the number 3. So, t3.
- If you are solving for the 10th term, simply replace the n in tn with the number 10. So, t10.
If you are solving for the 150th term, what variable could you use to refer to this term? ![]()
Look at the definition of Sequence. Compare this definition with the one you already added to your copy of Module 1 Glossary Terms. You may want to revise or add to your definition. Scroll down through Sequence and read the “More” section.
As you read the definition, pay particular attention to the following:
- What is the difference between a finite sequence and an infinite sequence?
- How is the tn notation used?
- How do you use notation to distinguish finite and infinite sequences?
Add what you have learned about finite and infinite sequences to Module 1 Glossary Terms.
Self-Check 1
Refer to the definitions of the variables a, d, n, and tn to answer the following questions.
Consider the sequence 20, 18, 16, 14, 12, 10, 8.
1.9. Explore 5
Module 1: Sequences and Series
Try This 4
Now that you are familiar with the variables that will be used, you are ready to construct a formula. You will do this in two different ways. After constructing your formula, you will have an opportunity to share your discoveries and your strategies with others.
Part 1
- Complete a table like Table 1 by simplifying each of the formulas. Record your answers under the Simplified Form column.
TABLE 1: FORMULAS DESCRIBING SEQUENCES IN TABLE 1 Original Formula
Simplified Form
1
tn = −29 + (n − 1)(7)
2
tn = 2 + (n − 1)(3)
3
tn = n − 1
4
tn = 96 + (n − 1)(−10)
- Match each sequence in Table 2 with its corresponding formula from Table 1. For example, if you think sequence A is described by formula 3, then you would write “A3” in your copy of Table 2.
TABLE 2: EXAMPLES OF ARITHMETIC SEQUENCES Sequence
Formula from Table 1
A
0, 1, 2, 3, ...
B
2, 5, 8, 11, ...
C
96, 86, 76, 66, ...
D
−29, −22, −15, −8, ...
- What strategies did you use to determine how the formulas matched the sequences?
- What patterns do you see between the original formulas and the properties of sequences?

- Based on the pattern you observed, what would the formula to describe the following sequence look like?
23, 31, 39, 47, 55, ...
- Study the relationship between the sequences and their corresponding simplified formulas (found in the last column of Table 2). How could you construct a formula in the simplified form without writing the formula in the original form?
Part 2
In Part 2, consider an arithmetic sequence that begins with the term a and has a common difference d.
Watch Arithmetic Sequence Video for an explanation of the table in question 7.
- Complete the table by writing an expression for t1, t2, t3, t4, t5, and t6 in terms of a and d. Simplify the expression. The first three rows have been completed for you.
n
tn
Expression
1
t1
a
2
t2
a + d
3
t3
a + d + d or a + 2d
- Describe the relationship between n and the coefficient of d in the expression. Express the relationship using the variable n.

- Extend the pattern you noticed in the table. What would be the expression for t20?
- What would be the expression for tn?
![]() Save your results in your course folder.
Save your results in your course folder.
1.10. Explore 6
Module 1: Sequences and Series
General Term of the Sequence
From working through Try This 4, you may have discovered that you can find the value of any term in an arithmetic sequence by using the formula tn = a + (n − 1)d.
This formula is called the general term of the sequence. As with any formula, if you are given values for all but one variable, you will be able to solve the equation for the unknown variable. In the remainder of the lesson you will use the general term to determine tn, a, n, and d.
Throughout this course you will learn many formulas for solving problems. Use the document Formula Sheet, or a tool recommended by your teacher, to keep track of these formulas. You will use Formula Sheet to review all of the formulas at the end of each module and to prepare for your final assessment.
![]() Save Formula Sheet in your course folder now.
Save Formula Sheet in your course folder now.
You will update this document throughout Mathematics 20-1. For now, add the formula for the general term of the sequence to your copy of Formula Sheet.
Share 2
Retrieve your results from Try This 1. In that activity you studied arrangements of marbles in three figures, as shown in the illustration. You discovered a pattern and used that pattern to determine the number of marbles in subsequent arrangements.

You used a method for determining the number of marbles in figure 20 and in figure 100. If possible, work with a partner on the following questions, and then share your work with a group.
- If t1 = 10 marbles, t2 = 14 marbles, t3 = 18 marbles, and so on, what is the value of tn if n is the figure number? (In other words, construct a formula that will allow you to find the number of marbles in any given figure.)
- Share your formulas with other groups. Record any formulas that are different from yours. Verify that these formulas will lead to the correct answer.
- With your partner, evaluate the advantages and disadvantages of each of the formulas you have learned. Be sure to talk about
- the complexity of the formula
- the variables required in each formula
- the ability to use the formula for both small and large values of n.
- the complexity of the formula
![]() If required, save a copy of your discussion in your course folder.
If required, save a copy of your discussion in your course folder.
1.11. Explore 7
Module 1: Sequences and Series
Example 3
Work through Dakota’s Example. The general term of the sequence formula will be used to help solve the problem. You might recognize the question from the beginning of Explore.
Self-Check 2
Assume that, at age 17, Dakota gets a part-time job earning $12/h. He receives a signing bonus of $250 when he begins his job.

Stockbyte/Thinkstock
- Complete the table relating Dakota's earnings to the number of hours worked.
Number of Hours Worked Earnings ($) 0 250 1 262 2 3 4 5
- Identify the a and d in the arithmetic sequence represented by the earnings column. Answer
Be careful when you establish the value of a. Remember that a is the same as t1. What do you want t1 to represent in this problem?
- Write the general term representing this situation. Answer
- Show how you would use the general term to determine the number of hours Dakota needs to work to earn $1270. Answer
Go to the textbook for additional examples demonstrating how you can use the general term to determine properties of an arithmetic sequence. Turn to page 10 to view “Example 1.” Look at “Method 1” only. Then turn to page 12 to view “Example 2.” Work through each example and pay attention to
- where given values in the problem are substituted into the formula
- the difference between how you should interpret n versus tn
Compare the solution strategies demonstrated in the textbook examples to Example 3, which you looked at in the video about Dakota's earnings.
![]() In your course folder, write down the points the textbook examples have added to your understanding of arithmetic sequences.
In your course folder, write down the points the textbook examples have added to your understanding of arithmetic sequences.
Self-Check 3
Use Arithmetic Sequences Mini-Quiz to check your understanding of arithmetic sequences.
1.12. Connect
Module 1: Sequences and Series
In the Lesson 1 Assignment you will demonstrate your understanding of the lesson outcomes. You will apply the concepts and strategies you learned to new situations. You must show your work to support your answers.
Open your copy of Lesson 1 Assignment, which you saved in your course folder at the beginning of this lesson. Complete the assignment.
Project Connection
You are ready to start working on Module 1 Project: Financing Your Dreams. You will complete a part of the Module 1 Project in each lesson. Review the following sections to become familiar with what you will be doing throughout the project and how you will be assessed:
- Introduction
- Overview
- Project Presentation
- Rubric
Still in Module 1 Project: Financing Your Dreams, complete Project Connection 1: Financial Goals.
![]() Save all your work in your course folder.
Save all your work in your course folder.
Going Beyond
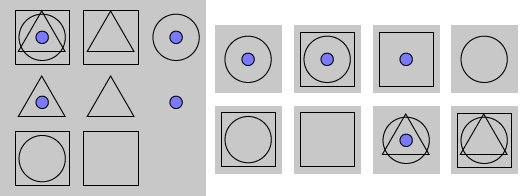
Have you written an IQ test? Maybe in school or on the Internet? IQ tests measure a person’s reasoning ability. They often contain questions that test a person’s ability to uncover patterns. Can you identify the pattern in the sequence of diagrams shown in the illustration? Can you sketch the next figure in the progression?
Search the Internet using keywords like “online IQ test” or “international high IQ” to find examples of questions that test your ability to sequence. Can you find questions based on arithmetic sequences?
Try some of the free online IQ tests. Try to improve your score by taking the test multiple times. Many of the IQ tests draw on a bank of questions. Even if you retake the test, you may see a different set of questions. Eventually you will recognize repeating questions, and you will be able to respond more quickly. Does the IQ test reward you for both how quickly and how accurately you respond? Test your hypothesis.
![]() Copy your favourite questions into your course folder.
Copy your favourite questions into your course folder.
You can try these questions out on family and friends!
1.13. Lesson 1 Summary
Module 1: Sequences and Series
Lesson 1 Summary

© Geesfrosh/20634221/Fotolia
In this lesson you investigated the following questions:
- How can you find any term in an arithmetic sequence?
- How are patterns important in the real world?
You studied number patterns called sequences. Specifically, you learned about the properties of arithmetic sequences, You derived a formula, called the general term, that can be used to represent any arithmetic sequence and determine its properties.
You relied on your ability to discover patterns and relationships among numbers. Finding and using patterns is important in mathematics. Many of the formulas you see in math are descriptions of patterns.
Patterns are also important in daily living. Accurate weather forecasting, for example, is something people depend on to plan their business and recreational activities. In the entertainment industry, television series are cancelled, extended, or moved to other time slots based on audience viewing patterns.
In the next lesson you will investigate where arithmetic sequences are applied in real-world contexts. You will also discover how arithmetic sequences are related to linear functions.