Section 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-3 SS |
| Book: | Section 2 |
| Printed by: | Guest user |
| Date: | Tuesday, 2 December 2025, 6:58 AM |
Description
Created by IMSreader
Table of contents
- 1. Section 2
- 1.1. Lesson 1
- 1.2. Launch
- 1.3. Are You Ready?
- 1.4. Refresher
- 1.5. Discover
- 1.6. Explore
- 1.7. Explore 2
- 1.8. Explore 3
- 1.9. Explore 4
- 1.10. Explore 5
- 1.11. Connect
- 1.12. Lesson 1 Summary
- 1.13. Lesson 2
- 1.14. Launch
- 1.15. Are You Ready?
- 1.16. Refresher
- 1.17. Discover
- 1.18. Explore
- 1.19. Explore 2
- 1.20. Explore 3
- 1.21. Explore 4
- 1.22. Connect
- 1.23. Lesson 2 Summary
- 1.24. Lesson 3
- 1.25. Launch
- 1.26. Are You Ready?
- 1.27. Refresher
- 1.28. Discover
- 1.29. Explore
- 1.30. Explore 2
- 1.31. Explore 3
- 1.32. Explore 4
- 1.33. Connect
- 1.34. Lesson 3 Summary
- 1.35. Section 2 Summary
1. Section 2
Section 2: Slope—Rate of Change
Section 2 Introduction

© Pavle/9963375/Fotolia
Generating electricity using stored water provides energy to millions of people. The amount of water flowing through the turbines helps determine how much electricity is produced. The rate at which water is used has to be controlled, or there is a chance the storage area will be emptied.
In this section you will look at rates of change and ways to calculate these rates. You will use proportional reasoning and unit analysis, and you will use both methods together. With these methods you will be able to solve problems in either the imperial or the SI measurement system. You will see that there are often safety issues associated with slopes and rates of change.
1.1. Lesson 1
Section 2: Slope—Rate of Change
Lesson 1: Rate Problems—Unit Analysis
Focus

wheelchair racers: © Peter Parks/Getty Images; Svetlana Masterkova: © George Gobet/Getty Images
In this lesson you will look at rates of change. The time it takes to move a distance, also known as speed, is an example of a rate of change. As you move through Lesson 1 you will see that slopes can describe rates of change.
Shelly Woods is a British wheelchair racer who set a women’s world record time of 3:21.22 min in the 1500-m race. Svetlana Masterdova of Russia is a world record holder who ran 1000 m in 2:28.98 min. Who was moving at a faster speed? How can you compare the times when the distances are different?
As you looked at the two racing photos, did you notice the differences in safety equipment? Why is the type of protective equipment different?
Lesson Questions
In this lesson you will investigate the following questions:
- How is unit analysis used to solve problems?
- How does slope describe a rate of change?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share Sections of the lesson
- your contribution to the Mathematics 20-3: Glossary Terms and the Formula Sheet
- Lesson 1 Assignment (Save a copy of your lesson assignment document to your course folder now.)
- the Project Connection
1.2. Launch
Section 2: Slope—Rate of Change
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 1.
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.3. Are You Ready?
Section 2: Slope—Rate of Change
Are You Ready?
- Complete the following calculations.
-
Complete the Time Matching activity by matching the times that are equal but have different units.
If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions difficult, complete Refresher to review these topics.
1.4. Refresher
Section 2: Slope—Rate of Change
Refresher
If you don’t know the answers in Are You Ready?, or require more information, then use the following links to help you. Choose one of these two links. The first is an interactive lesson on fractions, the second is a text-based lesson on fractions from an apprenticeship carpentry independent learning module.
- Basic Math Concepts - Part B
Go to page 7, example 1
Go to page 8, example 3
Go to page 10, example 2
Go to page 10, Rules for Multiplication and Division of Fractions
This refresher link deals with a conversion of Basic Units of Time.
Go back to Are You Ready? and try the questions again. Contact your teacher if you continue to have difficulty.
1.5. Discover
Section 2: Slope—Rate of Change
Discover
By using the Unit Conversion applet in Try This 1, you will discover what unit analysis is by investigating problems.
Try This 1
- Open the Unit Conversion applet to complete some unit conversions.
- Create three problems of your own and solve them. Make sure one of your problems takes at least two steps to solve.
-
As of October 2010, Mischo Erban of Vernon, British Columbia, held the world record as the fastest downhill skateboarder at 36.11 m/s.

© Ezra Shaw/Getty Images
While you may be familiar with speeds like 36.11 m/s, other people may not. In the United States, feet are used for measurement, not metres. To share Erban’s record with an American friend, you’ll want to change the measurement to feet per second.
![]() Save your responses to your course folder.
Save your responses to your course folder.
1.6. Explore
Section 2: Slope—Rate of Change
Explore
In Discover you used a specific applet to convert units through unit analyis. There are many ways to convert units.
- Use a specific applet, as you did in Discover.
- Harness the power of a search engine, like Google.
- Understand the calculations that are required and do these calculations yourself whenever or wherever you are.
Try This 2
Enter “36.11 m/s to ft/s” into the Google® search box.
Google has a calculator that does these kinds of unit changes. How did the answer from Google compare with the answer from question 3 of Try This 1? Try converting 36.11 m/s to some other units of speed.
Unit Analysis Calculations
Conversions require some knowledge about how different measures are related to each other and how to multiply fractions. For example, to change metres/second to feet/second, you would do the following:
Step 1: Look up the conversion for metres to feet and find that 1 m = 3.280 839 9 ft. You might also have found the conversion to be either ![]() or
or ![]() . These are sometimes referred to as conversion factors. When you multiply by a conversion factor, you are really just multiplying by 1. Watch Conversion Factors to see the proof!
. These are sometimes referred to as conversion factors. When you multiply by a conversion factor, you are really just multiplying by 1. Watch Conversion Factors to see the proof!
Step 2: Determine what conversion factor you must use. The conversion factor with the metres in the denominator will allow you to cancel out the metres in the numerator of the original units, ![]() .
.
Step 3: Multiply the factor, and cancel out units found in both the numerator and denominator.
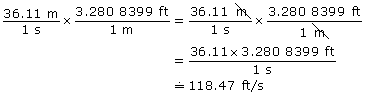
This three-step method is more work for you than using a search engine, but you can see exactly how the units change and you can do the conversion even if there isn’t a computer handy.
You may remember from Discover that some conversions take two or more steps. A conversion like 36.11 m/s = 80.775 769 5 mi/h requires many steps. You’ll notice that two units need to be changed—distance and time.
![]()
1.7. Explore 2
Section 2: Slope—Rate of Change
Self-Check 1
- Use one of the following conversion factors to show that 36.11 m/s = 1421.653 54 in/s.
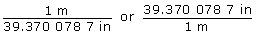
Need help getting started?
Answer
- Use the following information to show a calculation that converts 36.11 m/s into 80.775 769 5 mi/h.
You can use the following conversion factors to help you:
0.000 621 371 192 mi = 1 m
3600 s = 1 h
Need some help getting started?


Answer
Did you notice that the m and the s disappeared in your calculations? Why did they disappear? ![]()
Many of the measurements in the lesson have had units that were made up of or showed a relation between two units. For example, in 36.11 m/s, the unit of metres has been related to seconds. When you write a ratio with two different units, it’s called a rate. In Try This 3 you will see how a rate is related to slope and how unit analysis can help some rate problems.
Try This 3
The skateboarder from the Discover section was moving at a speed of 36.11 m/s. How far could he travel in one minute?
- Calculate the answer by completing this chart. If the skateboarder has a speed of 36.11 m/s, then he must move a distance of 36.11 m every second.
Time (s) Distance (m) 0 0 1 36.11 2 72.22 = (36.11 + 36.11) or (36.11 × 2) 3 = (36.11 + 36.11 + 36.11) or (36.11 × 3) • • • • • • 59 = (36.11 × 59) 60 = (36.11 × 60)
While this chart works, it is time consuming. You might prefer to graph a few points from the chart. You’ll be able to see the distance increase each second.
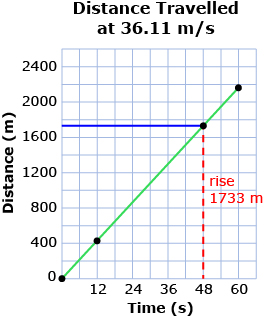
Notice how the blue line in the graph helps. This line connects the point on the green line to the vertical axis at 48 s. This lets you read the value of the distance. The graph lets you get an answer of about 1733 m travelled in 48 s.
- What is the slope of the green line?

- How does an understanding of unit analysis help you figure out that the speed, 36.11 m/s, has to be multiplied by 60 s and not divided by 60 s to find the total distance travelled in 60 s? What would happen if you had divided by 60 s?
![]() Save your responses to your course folder.
Save your responses to your course folder.
Convert seconds to hours like this.
![]()
Did you notice that the s disappeared in this calculation?
First, convert metres to miles like this.
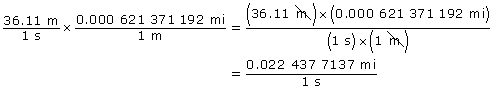
Did you notice how the metres cancelled and miles were left?
Do this as a two-step process. Perhaps start by changing metres to miles.
![]()
You complete the conversion by changing seconds to hours.
Begin like this:
![]()
1.8. Explore 3
Section 2: Slope—Rate of Change
In Try This 3 you may have noticed the connection between a rate of speed and the slope of a graph of the rate. The slope of the distance versus time graph is the same as the speed (rate).
In Try This 4 you will investigate another rate: the number of rotations per minute. You will examine how the speed of the car relates to the size of the wheels and the number of times the wheels turn.

sportscar: Hemera/Thinkstock; sedan: Hemera/Thinkstock
Try This 4
A sports car has a wheel diameter of 20 in. A sedan has a wheel diameter of 17 in. If both cars are travelling at the same speed, which car’s wheels will rotate faster?
- The interactive Sedan Chart shows wheel rotations for the sedan. Complete the table by adding a number and then pressing the Enter key. Each time you press Enter, a point will be added to the graph. You will then see the slope of the line the points define.
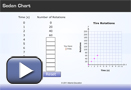
- From the table and graph, you can see that in 1 s, the tires rotate 20 times. This gives a conversion factor that looks like
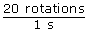 . It’s read as “20 rotations per 1 s.” This fraction form is a rate. How does this rate compare to the slope of the graph?
. It’s read as “20 rotations per 1 s.” This fraction form is a rate. How does this rate compare to the slope of the graph? 
The slope is a unit rate since the denominator is 1 s. You can use this unit rate and unit analysis to calculate the number of wheel rotations for any number of seconds. For example, what follows is the calculation for 8 s.
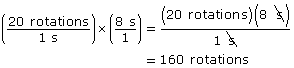
The seconds are abbreviated as s in the numerator and denominator to make it easier to cancel them and leave only the rotations unit.
- Complete the interactive Sports Car Chart and graph for the sports car.
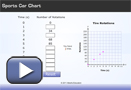
Since you aren’t given the information for 1 s, you need to find the unit rate. Calculate the slope of the graph which will be the unit rate.

 How does the calculated slope compare with the answer from the graph?
How does the calculated slope compare with the answer from the graph?
Self-Check 2
- Refer to the Sports Car Chart and, from the graph, estimate the number of rotations the sports car's wheels made in 9 s. Answer
- Calculate, using the rotation rate for the sports car, the number of rotations the sport car's wheels made in 9 s. Answer
- How do your answers compare?
 Answer
Answer
- Refer to the Sedan Chart and, from the graph, estimate how many rotations the sedan's wheels made in 6.5 s. Answer
- Calculate, using the rotation rate for the sedan, the number of rotations the sedan's wheels made in 6.5 s. Compare your answer with your estimate. Answer
- Answer the following.

For example, use the data for 4 s and 2 s to find the slope of the graph.
1.9. Explore 4
Section 2: Slope—Rate of Change
To this point you have only been multiplying by conversion factors to solve problems. But in reality you may find cases where you need to divide by a conversion factor.
A Swedish motorist was caught speeding on a motorway (highway) in Switzerland. He was driving close to 300 km/h! That is almost the distance from Edmonton to Calgary, and he would have gone this distance in about ONE hour (maybe a little longer, but not much longer).
The fine he had to pay was about $1 million. His excuse was that the speedometer was not functioning properly!
Example

© aleksey ipatov/23629605/Fotolia
It’s not just in the summer that people move quickly down a hill. Darren Powell holds the world record for speed snowboarding, at 56.08 m/s. (It’s not your regular fun slide down a hill.)
Use Powell’s world record speed to determine how long it would take him to complete a 500-m race. Here is one way to determine the answer.
His speed of 56.08 m in 1 s can be used as a conversion factor; either as ![]() .
.
Then 500 m will take him how many seconds?
You could also think how many 56.08 m are there in 500 m. You would then do the following:

1.10. Explore 5
Section 2: Slope—Rate of Change

Brand X Pictures/Thinkstock
Example
Go to a search engine and type in the words “world’s fastest texter” and “gumballtech.” You will watch an expert text the following two sentences:
- The razor-toothed piranhas of the genera Serrasalmus and Pygocentrus are the most ferocious freshwater fish in the world. In reality they seldom attack a human.
How good are you at texting? While using a device capable of texting, time how long it takes you to text the same two sentences.
How long did it take you (in seconds) to type the sentences?
There are 26 words in the paragraph (punctuation doesn’t count).
Calculate the number of words you text in one second (unit rate).
Start with ![]() and change to an equivalent fraction with 1 s in the denominator
and change to an equivalent fraction with 1 s in the denominator ![]() .
.
For example, if you took 135 s to text the two sentences, you would do the following.
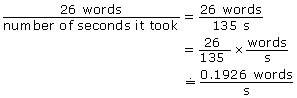
You can use your calculator to change the fraction to a decimal.
You can check your method with the Texting activity.
Stockbyte/Thinkstock
Self-Check 3
- Calculate your texting speed as a unit rate in words per second. Answer
- Pulleys are used to operate many types of things, including elevators and sails on a boat. Pulleys transfer rotation from one part of a machine to another by rotating and, like wheels, the smaller the diameter, the faster they rotate.
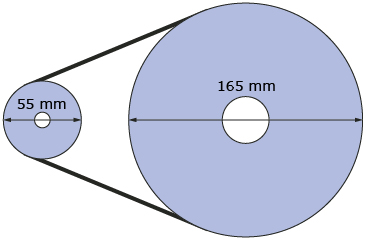
The smaller pulley, which has a 55-mm diameter, has a speed of 120 rpm. Determine the number of seconds for 1 revolution: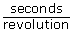 . Answer
. Answer
It is now time to add new math terms to Mathematics 20-3: Glossary Terms.
In this lesson the new terms you will add are
- unit analysis
- conversion factor
- rate
1.11. Connect
Section 2: Slope—Rate of Change
Connect
Project Connection
![]() You are now prepared to begin working on Step 4 of the Module 3 Project: Luge Track Comparison. Make sure to save all your project work in your course folder to submit at the end of Section 2.
You are now prepared to begin working on Step 4 of the Module 3 Project: Luge Track Comparison. Make sure to save all your project work in your course folder to submit at the end of Section 2.
Lesson 1 Assignment
Your lesson assignment contains some problems for you to solve using the knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies learned to a new situation. Show work to support your answers.
Open the Lesson 1 Assignment that you saved to your course folder and complete the questions.
1.12. Lesson 1 Summary
Section 2: Slope—Rate of Change
Lesson 1 Summary

© Laurent Renault/4573608/Fotolia
In this lesson you learned how to use unit analysis to solve a variety of rate problems. You saw how you could find unit rates by looking at the slopes of graphs. You applied your understanding of unit analysis and the multiplication and division of fractions to get desired units in calculations, and conversion factors were used that let you cancel units.
1.13. Lesson 2
Section 2: Slope—Rate of Change
Lesson 2: Rate Problems—Combining Strategies
Focus

Hemera/Thinkstock
Rob Thomson skateboarded 12 159 km around the world in 850 days. This adds up to almost 2.5 years! The trip cost him a total of $16 000, or approximately $18.82 per day.
The skateboarding experience involved visiting many places, experiencing interesting things, and meeting unique characters. Using the strategy of unit analysis or proportional reasoning, you can calculate that Rob travelled 14.30 km per day. The assumption is that Rob skateboarded every day. Do you think he did?
In this lesson you will learn how strategies of unit analysis and proportional reasoning can help you solve problems.
Lesson Question
In this lesson you will investigate the following question:
- How are proportional reasoning and unit analysis used to solve rate of change problems?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your contribution to the Math 20-3: Glossary Terms and the Formula Sheet
- Lesson 2 Assignment (Save a copy of your lesson assignment document to your course folder now.)
- the Project Connection
Materials and Equipment
- calculator
1.14. Launch
Section 2: Slope—Rate of Change
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete this lesson.
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.15. Are You Ready?
Section 2: Slope—Rate of Change
Are You Ready?
- Click on the play button to launch Rates. These questions will check your understanding of unit rates.
- Click on the play button to launch Ratios and Proportions. Complete the questions to check your understanding of ratios and proportions.
If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions difficult, complete Refresher to review these topics.
1.16. Refresher
Section 2: Slope—Rate of Change
Refresher
If you had difficulty with the rate, ratio, and proportion activities in Are You Ready?, go to the following links for review.
 Click the play button to launch Rate.
Click the play button to launch Rate.
 Click the play button to launch Ratio.
Click the play button to launch Ratio.
 Click the play button to launch Proportion.
Click the play button to launch Proportion.
Go back to Are You Ready? and try the questions again. Contact your teacher if you continue to have difficulty with the questions.
1.17. Discover
Section 2: Slope—Rate of Change
Discover

© Tommy Schultz/4822167/Fotolia
The following Try This activity lets you explore the ratio of lifeguards to swimmers.
Try This 1
Use Kids at the Pool to help answer the questions that follow.
- What is the ratio of swimmers to lifeguards?
- If the pool is at its capacity of 500 swimmers, what is the minimum number of lifeguards the pool manager must have on deck? Complete a chart like the one that follows.
Lifeguards Swimmers 2 50 4 100 200 300 400 500
- Examine the numbers in the table. Can you see a way to use the 1:25 lifeguards-to-swimmers ratio to help find the ratio when the pool is full to capacity (x:500)? Describe a strategy you could use to answer this question without the table.
![]() Save your responses to your course folder.
Save your responses to your course folder.
Share 1
Compare your answers to Try This 1 with a partner or with a group of people. How did the different strategies compare for question 3?
- Make a list of all the strategies used.
- Did anyone use a similar strategy to your own?
- Test each strategy by finding the number of lifeguards required for 1000 swimmers.

- Which strategies worked? Do you prefer one strategy over another?
![]() Save the list of strategies to your course folder for future reference.
Save the list of strategies to your course folder for future reference.
1.18. Explore
Section 2: Slope—Rate of Change
Explore
In Discover you developed strategies to help solve a ratio problem. You found a known ratio, 1:25, for lifeguards to swimmers. Then you used this ratio to find an unknown ratio, x:500.
One strategy to solve the problem may have been using a proportion to compare the two ratios.
![]()
Once a proportion is set up, you can rearrange or cross multiply to solve for x.
Rearrange
|
Cross Multiply
|
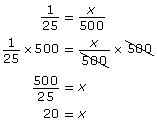 |
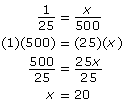 |
As you saw in Discover, 20 lifeguards are needed when 500 people are swimming.
As you have just seen, proportional reasoning helps relate one known ratio to find a missing term in another ratio. In Try This 2 you will use proportional reasoning to solve a problem.
1.19. Explore 2
Section 2: Slope—Rate of Change
Try This 2

© Horticulture/2658120/Fotolia
Aron is working with a grass trimmer. She has to mix oil with gasoline in a 1:50 ratio. Aron needs to have at least 5 L of mixture to complete her day’s work. If she started with 5 L of gasoline, how much oil would Aron have to add?
- Set up a proportion to represent this question. You know the following:
- The oil to gasoline ratio is 1:50.
- There is 5 L of gasoline added.
- The amount of oil is unknown; let it be x.

- Solve your proportion by rearranging or cross multiplying to find x.

![]() Save your responses to your course folder.
Save your responses to your course folder.
Self-Check 1
-
The company Aron is working for has ten other workers using grass trimmers. The company decided to do the mixing in one large container. It is hoped there will be enough of the gas-oil mixture to last the workers a week. In making the mixture, 5.8 L of oil were used. How much gasoline was used? Answer
-
Sam needs some cookies for a bake sale at school. Money is being raised for a nearby elementary school’s hot lunch program. He found this simple shortbread cookie recipe on the Internet. The problem is that the recipe makes only 8 cookies, and Sam needs 24 cookies. Use proportional reasoning to find the quantities of flour, sugar, and butter needed to make 24 cookies. Answer

© Michael Felix/7291730/FotoliaShortbread Recipe
-
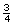 cup flour, sifted
cup flour, sifted -
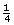 cup superfine sugar
cup superfine sugar 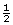 cup room temperature butter
cup room temperature butter
-
Rearrange
|
Cross multiply
|
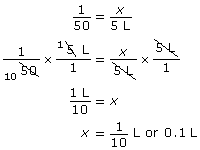 |
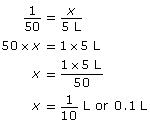 |
Aron would have to add 0.1 L (or 100 mL) of oil to the 5 L of gasoline.
1.20. Explore 3
Section 2: Slope—Rate of Change
In Try This 3 you will use proportional reasoning and unit analysis to solve a rate problem.
Try This 3
Many people enjoy riding zip lines.

Used with permission of Richard Wilson.
The zip line shown in the photo is 162 m in length, and the ride takes about 20 s. The average speed of a rider is ![]() .
.
- Set up a proportion to determine the average speed of a rider on the zip line in m/s (metres/second).


- Sketch a graph of the distance travelled over time. Use the sample graph paper.
- Suppose you want to express the average speed in question 2 in meters per minute
 .
.
-
Using unit analysis, what conversion factor will you use to get rid of seconds and end up with minutes?

- Convert the average speed in question 2 into metres per minute.

-
Using unit analysis, what conversion factor will you use to get rid of seconds and end up with minutes?
![]() Save your responses to your course folder.
Save your responses to your course folder.
Share 2
Share your graph from question 2 of Try This 3. Compare your responses to two other student responses.
- What is the slope of your graph?
- How does the slope compare to your answer for question 1?
![]() Revise your response if needed, and save your response to your course folder.
Revise your response if needed, and save your response to your course folder.
Rearrange
|
Cross multiply
|
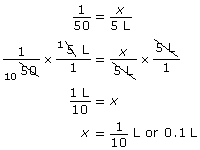 |
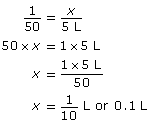 |
Aron would have to add 0.1 L (or 100 mL) of oil to the 5 L of gasoline.
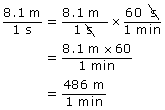 or
or 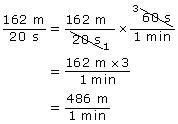
The speed is 486 m/min.
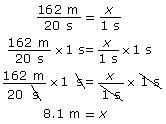
The average speed of the zip line rider was 8.1 m/s.
1.21. Explore 4
Section 2: Slope—Rate of Change
In Focus, Rob averaged 14.30 km/day on his skateboard. Skateboarding isn’t the most efficient method to move quickly over long distances, but it is a healthy way to travel. There are faster ways than skateboarding to get from one place to another on wheels. For example, passenger trains can move a large number of people quickly and efficiently.

bullet train: Comstock/Thinkstock;
steam train: © sumnersgraphicsinc/11284076/Fotolia
Trains have changed tremendously from the first steam-powered trains in the early 1800s. The fastest trains now are powered by electric motors. The CRH380 in China, with a maximum speed of about 420 km/h ![]() , is currently the fastest bullet train in the world. This train could take you from Edmonton to Calgary (about 300 km) in less than 1 h!
, is currently the fastest bullet train in the world. This train could take you from Edmonton to Calgary (about 300 km) in less than 1 h!
 Click on the play button to do the Blink activity.
Click on the play button to do the Blink activity.
In Blink, you saw that ![]() represents the speed of the bullet train, but so do these fractions:
represents the speed of the bullet train, but so do these fractions:
![]() ,
, ![]() , and
, and ![]()
They are all equivalent speeds, even though the units and numbers in the numerators and denominators vary.
It is now time to add new math terms to Mathematics 20-3: Glossary Terms.
In this lesson the new term you will add is
- proportional reasoning
1.22. Connect
Section 2: Slope—Rate of Change
Connect
Project Connection
![]() You are now prepared to begin working on Step 5 of the Module 3 Project: Luge Track Comparison. Make sure to save all your project work in your course folder to submit at the end of Section 2.
You are now prepared to begin working on Step 5 of the Module 3 Project: Luge Track Comparison. Make sure to save all your project work in your course folder to submit at the end of Section 2.
Lesson 2 Assignment
Your lesson assignment contains some problems for you to solve using the knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies learned to a new situation. Show work to support your answers.
Open the Lesson 2 Assignment that you saved to your course folder and complete the questions.
1.23. Lesson 2 Summary
Section 2: Slope—Rate of Change
Lesson 2 Summary

© Arto/23216514/Fotolia
Proportions show up in many different careers. The worker in this photograph is carefully adding a small amount of one chemical into a flask containing another chemical. Getting the proportions of chemicals correct can be a matter of life and death.
In this lesson you explored how to use proportional reasoning and unit analysis to solve problems. You found that a variety of different strategies can help you solve rate problems.
1.24. Lesson 3
Section 2: Slope—Rate of Change
Lesson 3: Rate Problems—Imperial and Metric Systems

Corrine Gailloux. Jim Milina: © All rights reserved.
Focus
Have you ever accomplished a goal that you thought was impossible? Imagine climbing a mountain. Now imagine climbing a mountain in a wheelchair! Many people, including Canadian Jim Milina (shown in the photo on the right), have climbed mountains in wheelchairs.

Hemera/Thinkstock
Mount Kilimanjaro is a mountain in Tanzania that Jim Milina climbed in his customized wheelchair with the help of friends and local guides. What reasons can you think of for using a special wheelchair for Jim’s climb?
Mount Kilimanjaro is 5895 m high from sea level to the summit. It is the highest point on the African continent.
Try this question to imagine just how tall this mountain is: If you were standing on each others' shoulders, how many people of the same height as you would it take to be as tall as Mount Kilimanjaro? ![]()
How long do you think it would take to climb Mt. Kilimanjaro? If you knew how long this journey would take, you could then make daily plans for
- how many kilometres you would climb
- how long of a rest you would take
- how much food and water you would need
Lesson Question
- How are tables used to solve rate problems that move between metric and imperial systems?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your contribution to the Math 20-3: Glossary Terms and the Formula Sheet
- Lesson 3 Assignment (Save a copy of your lesson assignment document to your course folder now.)
- the Project Connection
Materials and Equipment
- calculator
- measuring tape
1.25. Launch
Section 2: Slope—Rate of Change
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete this lesson.
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.26. Are You Ready?
Section 2: Slope—Rate of Change
Are You Ready?
- Check your understanding of equivalent units in the metric and imperial systems with SI-Imperial Conversions.
- Sort the units from question 1 as either metric units or imperial measurement units in SI-Imperial Sorter.

If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions difficult, complete Refresher to review these topics.
1.27. Refresher
Section 2: Slope—Rate of Change
Refresher
If you had trouble with the Are You Ready? questions, use the following links to help you.
Click on the play button to launch International System of Units. It provides information about units in the metric system. There is also a conversion applet that can be used to convert between units.
This second link provides a review of the imperial system and conversions within it and the SI system from Mathematics 10-3: Module 2.
Go back to Are You Ready? and try the questions again. Contact your teacher if you continue to have difficulty with the questions.
1.28. Discover
Section 2: Slope—Rate of Change
Discover
Setting up a table is a helpful strategy for solving problems. Watch Desert Car Travel and then discuss the strategy used in Share 1.
Try This 1
- How did the proportions set up in the example question from Desert Car Travel differ from the proportions you set up in previous lessons?
- How does the table help to set up a proportion?
- Set up a different proportion using the same values as in the example. This result will still result in the same answer.
![]() Save your responses to your course folder.
Save your responses to your course folder.
Share 1
Compare your answers to Try This 1 with a partner or in a group.
How do the proportions you created compare with others? How is it possible that different proportions could lead to the same answer?
![]() If required, save a copy of your discussion to your course folder.
If required, save a copy of your discussion to your course folder.
1.29. Explore
Section 2: Slope—Rate of Change
Explore
In Discover you may have noticed there are different ways of setting up a proportion to arrive at the same answer. Using a table to set up a proportion instead of ratios is a strategy that can be helpful.
Try This 2
You can purchase a 5-lb bag of peanuts at the store for $2.10.
- Assuming that the price per pound doesn't change, how much will a 7-lb bag of peanuts cost?
- Use the table to set up a proportion and solve the question.
Cost Pounds First Bag $2.10 5 Second Bag x 7
- Create two ratios based on this problem. Use these ratios to set up a different proportion and solve the question.
- Use the table to set up a proportion and solve the question.
- What is the cost of peanuts per pound?
Self-Check 1
- The temperature dropped 15°C in the last 30 days. If the rate of temperature drop remains the same, how many degrees will the temperature drop in the next 10 days?
Temperature Drop (°C) Number of Days Initial Drop 15 30 New Drop x 10
Answer
- Graph the points from question 1 with number of days on the horizontal axis. Join the points and find the slope of the resulting line. What does the slope tell you about the temperature drop? Answer
1.30. Explore 2
Section 2: Slope—Rate of Change
In the next example, proportions will be used to convert within and between SI and imperial units. As you have seen, the proportions you set up may vary but they can lead to the same answer.
Example
Bern Goosen is from South Africa. He has been disabled since birth due to cerebral palsy. Bern climbed Mount Kilimanjaro in October 2007 in a specially designed wheelchair.
Goosen set a verified world wheelchair record for climbing to the summit of Mount Kilimanjaro. He took 6 days, 3 hours, and 20 minutes. Though the mountain is 5895 m tall, the actual distance that Bern climbed is 3885 m. He started the ascent from the mountain’s base, which left 2885 m to climb. This data is based on the route that he chose to use; other paths can be used. Note that the following graphic shows the Rongai Route that Bern used to climb the mountain.
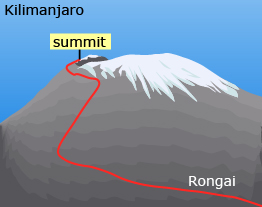
- Determine the distance climbed in kilometres.
The actual distance climbed in kilometres can be determined by using a Climbing Table to set up a proportion based on the relationship 1 km = 1000 m.

- Find the number of miles Bern Goosen climbed based on the number of kilometres calculated in question 1. You can use the Mile Climbing Table for assistance.
You will use proportional reasoning starting from the relationship that 1 km = 0.6214 mi (rounded to the thousandths).
1.31. Explore 3
Section 2: Slope—Rate of Change
Self-Check 2

Hemera/Thinkstock
When you are asked your height, do you answer in feet and inches or do you answer in metres and centimetres? Can you answer using both systems?
- Using proportions and the relationship of 1 m = 3.281 ft (rounded to the nearest thousandth), convert your height from
Try This 3
It took Bern Goosen 6 days, 3 hours, and 20 minutes to climb the 3885 m from the starting point of Rongai Route to Uhuru Peak, the summit of Mt. Kilimanjaro. The climb started on October 9, 2007, at 12:40 p.m. and ended on October 15 at 4:00 p.m.
- To the nearest hour, how much time did Bern spend on his climb?

- Use proportional reasoning to find the average number of metres climbed each hour. Round your answer to the nearest metre.

Use your favourite search engine and a guided search to find video footage of a person, or people, climbing Mt. Kilimanjaro by wheelchair. You will see how challenging this climb can be. Use the search terms “wheelchair Kilimanjaro climb.”
After viewing the video, do you have a better understanding of why Bern’s climbing rate was only 26 m/h?
The proportion you use might look something like this.
![]()
Try turning each time unit into hours.
6 days = ? h
3 h = 3 h
20 min = ? h
Then total the number of hours it took Bern to climb the mountain.
1.32. Explore 4
Section 2: Slope—Rate of Change
Try This 4
There are fun ways to use tables and proportions.
- Here’s a simple puzzle related to proportions and tables. Can you find a solution? Can you find more than one solution?
Fill in the squares with the numbers 0, 1, 2, 3, 4, 5, 6, 7, and 8.
- Each number can be used only once.
- The sums of the rows have to be in the proportion 1:2:3.
- The sums of the columns have to be in the proportion 1:2:3.
- Each number can be used only once.
- Can you complete the following table? How many ways can you complete the table in a logical way?
1 7 2 11 3 13 4
![]() Save your responses to your course folder.
Save your responses to your course folder.
Share 2
Share your solution from question 2 of Try This 4 with a couple of other students. Did you all think the same way? If not, how did your ideas differ?
1.33. Connect
Section 2: Slope—Rate of Change
Connect
Project Connection
![]() You are now prepared to begin working on Step 6 and the summary of the Module 3 Project: Luge Track Comparison. Make sure to save all your project work in your course folder to submit at the end of Section 2.
You are now prepared to begin working on Step 6 and the summary of the Module 3 Project: Luge Track Comparison. Make sure to save all your project work in your course folder to submit at the end of Section 2.
Lesson 3 Assignment
Your lesson assignment contains some problems for you to solve using the knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies learned to a new situation. Show work to support your answers.
Open the Lesson 3 Assignment that you saved to your course folder and complete the questions.
1.34. Lesson 3 Summary
Section 2: Slope—Rate of Change
Lesson 3 Summary

© rgbspace/10903123/Fotolia
The height of your face is likely different than the heights of your friends’ faces. Do you have a tape measure that only measures in SI? If so, you need to know how to change measurements to the imperial system. This is something you learned to do in Lesson 3.
More generally, you learned to solve problems in the metric and imperial systems by using tables and proportions. You saw how adjacent rows in tables can help you set up proportions. You used these proportions to solve problems involving distance, weight, and speed.
1.35. Section 2 Summary
Section 2: Slope—Rate of Change
Section 2 Summary

© Ron Downey/2024978/Fotolia
The world is full of change. It can be sunny and dry one minute and rainy the next. Changes lead to questions like these:
- How quickly?
- How long?
- How do these changes compare?
In this section you used proportional reasoning and unit analysis to solve slope and rate problems. You saw how tables can help you set up proportions and noted that there is a connection between the slope of a graph and unit rates. You were able to give answers in both the imperial and SI measurement systems.
In the Module 3 Project: Luge Track Comparison, you looked at slopes of tracks and the consequences of the slopes. You compared the slopes of Canada’s two Olympic luge tracks with the safety requirements for tracks. You also compared the slopes of the two tracks and the speeds athletes reached on the tracks.