Lesson 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-3 SS |
| Book: | Lesson 1 |
| Printed by: | Guest user |
| Date: | Tuesday, 2 December 2025, 6:58 AM |
Description
Created by IMSreader
1. Lesson 1
Module 4: The Right Kind Of Triangles
Lesson 1: The Pythagorean Theorem

Photos.com/Thinkstock
Focus
The astronomer and mathematician Pythagoras is credited with the first formal proof of the theorem that bears his name: the Pythagorean theorem. However, this theorem was well known in Egypt, Babylonia, India, and China for at least 1000 years before Pythagoras. Nevertheless, many scholars consider Pythagoras to be one of the first true scientists and the founder of a secret society, the Pythagoreans. Members of this group believed that all reality was mathematical in nature. The Pythagoreans must have loved a good puzzle and they studied a wide range of disciplines, including music, geometry, religion, philosophy, and gymnastics!
In this lesson, you will expand on your skills from Mathematics 10-3 and look at the real world through the lens of the Pythagorean theorem.
Lesson Questions
In this lesson you will investigate the following questions:
- How are triangles sketched in two or three dimensions to represent a problem?
- How can the Pythagorean theorem be applied to real-life situations?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from Try This and Share
- your contribution to the Mathematics 20-3: Glossary Terms and Formula Sheet
- Lesson 1 Assignment (Save a copy of your lesson assignment to your course folder now.)
- the Project Connection
Materials and Equipment
- scissors
- geometry set
- glue stick
- calculator
1.1. Launch
Module 4: The Right Kind Of Triangles
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 1.
Launch will review the following topics:
- the characteristics of right triangles
- complementary angles
- the Pythagorean theorem
- slope
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.2. Are You Ready?
Module 4: The Right Kind Of Triangles
Are You Ready?
Use the sliders in Slope - Activity A to answer the following questions.
Screenshot reprinted with permission of ExploreLearning
- The red dot’s coordinates are (−2, 5) and the blue dot’s coordinates are (−6,−1).
- What is the rise?
- What is the run?
- What is the slope?
- The red dot’s coordinates are (−2, 5) and the blue dot’s coordinates are (6, −1).
- What is the rise?
- What is the run?
- What is the slope?
- The red dot’s coordinates are (−2, 5) and the blue dot’s coordinates are (6, 5).
- What is the rise?
- What is the run?
- What is the slope?
- The red dot’s coordinates are (−2, 5) and the blue dot’s coordinates are (−2,−1).
- What is the rise?
- What is the run?
- What is the slope?
Use this diagram to answer the following questions.
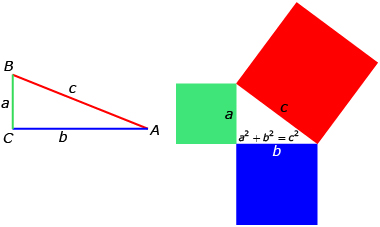
- Which two sides are the legs of
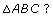 Answer
Answer
- What is the longest side of a right triangle called? Which side is it in the right triangle in the diagram? Answer
- The statement of the Pythagorean theorem is shown inside the triangle in the diagram. Explain what the statement means. Answer
- What is the sum of the measures of all three angles of
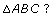 Answer
Answer
- What is the sum of the two acute angles? How do you know? Answer
- What special term is used to describe two angles that add up to 90°? Answer
- What is the slope of the hypotenuse? Answer
If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions to be difficult, complete Refresher to review these topics.
1.3. Refresher
Module 4: The Right Kind Of Triangles
Refresher
If you don’t know the answers to the questions in Are You Ready?, or if you require more information, work through the following activities to review right triangles, the Pythagorean theorem, complementary angles, and slope.
Pythagorean Theorem
|
|
Complementary Angles
|
|
Roller Coaster
|
Go back to Are You Ready?, and try the questions again. Contact your teacher if you continue to have difficulty with the questions.
1.4. Discover
Module 4: The Right Kind Of Triangles
Discover
The following puzzle is based on Henry Perigal’s 1830 proof of the Pythagorean theorem. Henry Perigal was so proud of this accomplishment that he had his theorem proof engraved on his tombstone!
Try This 1
You can try duplicating Perigal's proof by using either the multimedia or print option. After completing one of the options, answer questions 1 and 2.
Multimedia Option
Click on the Pythagorean Puzzle multimedia piece and follow the instructions to solve the puzzle.
Print Option
Print two copies of the Pythagorean Puzzle Template.
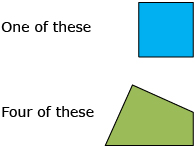
In the diagram there is a yellow right triangle. A square is drawn on each side of this triangle. The red lines divide the green square into four identical quadrilaterals.
From one copy of this diagram, carefully cut out the blue square and the green square. Then cut along the red lines of the green square. You should now have five puzzle pieces to work with.
Look at the part of the diagram that you did not cut. Fit the five puzzle pieces in the white square drawn on the hypotenuse of the yellow right triangle.
Now answer these questions.
- Were you able to fill in the white square using pieces of the smaller squares? Sketch the solution to your puzzle.
- Explain how this puzzle illustrates the Pythagorean theorem.
Share 1
Share your solution to the puzzle with a partner or with a group of students.
How do your explanations about how the puzzle relates to the Pythagorean theorem compare to the other students' explanations?
Refer to the Share Rubric. The rubric will help you understand what your teacher expects of you.
![]() Save a summary of your discussions and your solution to the Try This 1 questions in your course folder.
Save a summary of your discussions and your solution to the Try This 1 questions in your course folder.
1.5. Explore
Module 4: The Right Kind Of Triangles
Explore
The Pythagorean theorem states that for any right triangle, the square of the hypotenuse is equal to the sum of the squares of the two legs.
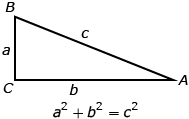
In this section you will apply the Pythagorean theorem in a variety of practical situations.
First, to be able to identify right-angled triangles in any context is important. Watch the video, Exploring the Pythagorean Theorem, and then answer the question that follows.
Share 2
Share three examples of right-angle triangles from real life with a partner or group. Think of examples not described in the video.
Try This 2

iStockphoto/Thinkstock
Carpenters use ladders on a regular basis. For safety, the foot of a ladder should be 1 ft away from the wall for every 4 ft up the wall the ladder reaches.
- Sketch the position of a ladder that reaches 4 ft up the wall. Include all measurements.
- To reach 12 ft up a wall, how far away from the wall must the foot of the latter ladder be positioned?

- Sketch a diagram showing the safe use of a ladder that reaches 12 ft up a wall. Identify the right triangle. Indicate the known measurements.
- In order to use a ladder safely, calculate the length of ladder required to reach 12 ft up a wall. Round your answer to one decimal place.
- What is the slope of this ladder? Will the slope be negative or positive?

![]() Save your responses to your course folder.
Save your responses to your course folder.
![]()
1.6. Explore 2
Module 4: The Right Kind Of Triangles
Self-Check 1

Digital Vision/Thinkstock
- One of the ziplines at Calgary’s Canada Olympic Park is 500 m in length and has a vertical drop of 100 m. Riders can reach speeds of 140 km/h.
- The foot of a 51-ft grain auger is positioned 40 ft from a grain bin. How high is the top of the auger above the ground? Round your answer to the nearest foot. Answer

© Westfield. Reproduced with permission.
Self-Check questions 1 and 2 involved the application of the Pythagorean theorem in two dimensions. Identifying Right-Angled Triangles in Real Life extends the theorem into three dimensions. As you watch the slideshow, note which scenarios are represented by right triangles in two dimensions and those that are in three dimensions.
iStockphoto/Thinkstock
Share 3
Discuss the following questions, based on Identifying Right-Angled Triangles in Real Life, with a partner or with a group of people.
- How many scenarios in the slideshow were represented by right triangles in three dimensions?
- What information would you use to explain or decide that a scenario must be represented by triangles in three dimensions instead of two dimensions?
Discuss any differences you may have and come to an agreement. Watch the slideshow again if necessary.
![]() Save a copy of the answers to your course folder.
Save a copy of the answers to your course folder.
1.7. Explore 3
Module 4: The Right Kind Of Triangles
Did you identify three different scenarios in Identifying Right-Angled Triangles in Real Life that were represented by right triangles in three dimensions? If not, go back and watch the slideshow again or contact your teacher.
The following example looks at how you might solve a problem involving right triangles in three dimensions.
Example

Jupiterimages/Comstock/Thinkstock
A javelin is 2.2 m long. A wooden storage chest is 2 m long, 80 cm wide, and 50 cm high.
- Show that this javelin cannot lie flat on the diagonal at the bottom of the chest.
- Can the javelin lie diagonally from one corner at the bottom of the storage chest to the opposite corner at the top of the chest?
Solution
-
Sketch and label your diagram.
- Let x be the diagonal distance across the bottom of the chest.
- The length of the bottom is 2 m.
- The width of the bottom is 80 cm or 0.80 m.
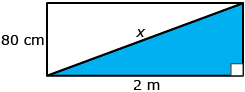
Use the Pythagorean theorem to find x.
c2 = a2 + b2
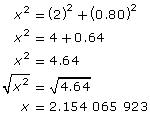
Because the javelin is 2.2 m long, it cannot sit flat along the diagonal at the bottom of the storage chest, which has a maximum length of 2.15 m.
x ≅ 2.15 m
-
Sketch and label your diagram.
The red triangle in this sketch can be used to find the diagonal through the centre of the storage chest.
- The legs are x and 50 cm long.
- The hypotenuse, d, is the diagonal distance through the centre of the chest.
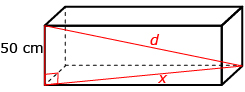
In part 1, you found that x is about 2.15 m. As before, you need all the measurements to be in the same units.
Convert 50 cm to 0.50 m.
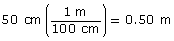
Use the Pythagorean theorem to find d.
c2 = a2 + b2
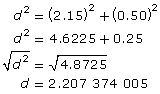
The javelin is only 2.2 m long and, therefore, shorter than the diagonal of 2.21 m.
The javelin will fit in the storage chest.d ≅ 2.21 m
Self-Check 2
In the javelin example, if one end is placed at one corner of the bottom of the storage chest, how high up along the opposite corner will the other end be? Round to the nearest centimetre. Answer
It is now time to add new math terms, definitions, examples, and notes to your Mathematics 20-3: Glossary Terms document. Complete the missing pieces of the document, and save it to your desktop. Note that some terms, definitions, examples, and notes have already been provided in the document.
In this lesson the new terms you will add are
- hypotenuse
- legs
At this time, you may want to add the Pythagorean theorem to your Formula Sheet.
- c2 = a2 + b2
1.8. Connect
Module 4: The Right Kind Of Triangles
Connect
Going Beyond
Here is another Pythagorean Puzzle. Print two copies of this puzzle. Cut out all the grey pieces from one copy. Use these seven pieces to cover the lower square on your second copy of the puzzle.
Project Connection
Begin the Module 4 Project: The Right Triangle—At Work and At Play.
You should
- read through the entire project: Introduction; Parts A, B, and C; and the Project Assessment
- complete Part A: At Play—The Tangram Puzzle
![]() Remember to save all your work to your course folder to submit at the end of the module.
Remember to save all your work to your course folder to submit at the end of the module.
Lesson 1 Assignment
Your lesson assignment contains some problems for you to solve using knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies that you have learned to a new situation. Show work to support your answers.
Open the Lesson 1 Assignment that you saved to your course folder and complete the questions.
1.9. Lesson 1 Summary
Module 4: The Right Kind Of Triangles
Lesson 1 Summary

Hemera/Thinkstock
The Pythagorean theorem, c2 = a2 + b2, is to mathematics as E = mc2 is to physics. Both of these formulas are important to their disciplines and tend to be remembered for a long time after the meaning of the formula has been forgotten.
In this lesson you reviewed the Pythagorean theorem and its application to a variety of two- and three-dimensional problems. You also had a chance to explore some puzzles involving right triangles and the Pythagorean theorem.