Module 4 Project

Module 4 Project: The Right Triangle—At Work and At Play

 

If you love puzzles or enjoy a good challenge at work, a solid understanding of right triangles will give you an advantage. In this project you will play with right triangles, solve puzzles, and identify and solve triangle-related problems you may run into in a future job.

 

At points during the Module 4 lessons, you will be encouraged to work on a step of the project in order to spread out the work over a few weeks. Save each of these steps to your course folder. The entire project and your self-assessment will be submitted to your teacher at the end of the module.

 

Time

 

The goal is to complete this project in less than six hours. Each lesson in the module will direct you to complete one or more of the steps.

 

Part A: At Play—The Tangram Puzzle

 

The tangram is an ancient puzzle that originated in China, where it is known as “the Wisdom Puzzle.” The tangram made its way to Europe and the Americas in the nineteenth century, when China opened up to trade.

 

The puzzle consists of seven pieces—five right triangles of various sizes, a small square, and a parallelogram. These seven pieces fit together to form a square. The object of the puzzle is to use the seven pieces to form various figures. The pieces must touch but cannot overlap. You are allowed to rotate the pieces and flip the parallelogram. The image below shows some of the figures you can form.

 

Hemera/Thinkstock

 

Your goal for this part of the project is to analyze the shapes of the tangram puzzle. You will use many of the skills you acquired in this module. These skills involve the Pythagorean theorem, similar right triangles, and right-triangle trigonometry.

 

You can form these shapes and many others using tangram software or you can make your own tangram pieces. Click on Interactive Tangram or scroll down on the instructions to make your own.

 

Interactive Tangram

 

Copyright © 2002 Philippe Banwarth

 

Making Your Own Tangram

 

Make a set of paper tangrams by folding paper. You will need scissors and a square sheet of paper or light cardstock measuring 20 cm on each side. Follow these directions.

 

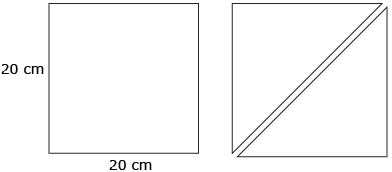
Step 1: Begin with a square sheet of paper measuring 20 cm on each side. Fold the square along a diagonal (shown in red). Then cut the square into two triangles along this line.

 

 

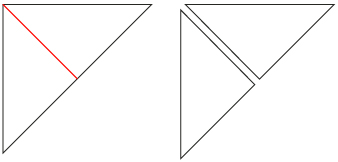
Step 2: Take one of the two right triangles and fold it in half. Then cut it along the line (shown in red) created by the fold. Set these two smaller right triangles aside. These are two of your tans (puzzle pieces).

 

 

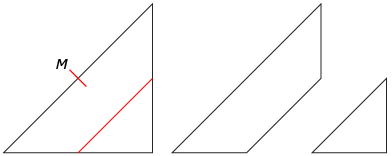
Step 3: Take the second large triangle from the Step 1, and lightly crease this triangle at the middle of its hypotenuse (shown in the diagram below as M). Then fold the right angle up to meet point M (the fold line is shown in red in the diagram below). Cut along this crease. Set the small right triangle aside. It is your third tan.

 

 

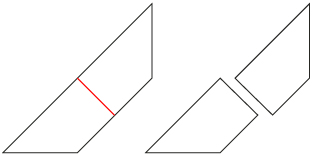
Step 4: Take the trapezoid from the third step. Fold it in half (shown in red). Cut the trapezoid in half along the crease.

 

 

Step 5: Take one of the two pieces created in Step 4, and fold the acute angle to the right angle (the fold line is shown in red below). Cut along this crease. Set the small triangle and square aside. These are two more tans.

 

 

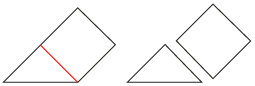
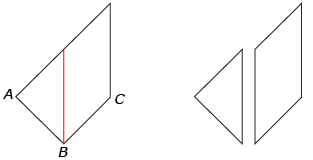
Step 6: Take the other piece created in Step 4 and fold it as shown below so that AB is on BC. Cut along the crease to get the last two tans!

 

 

1. Choose five of the twelve figures that follow. Use either “JTans,” the digital tangram interactive accessible by clicking on the play button, or the paper tangram set to create those five figures. You may be required to take a screen shot or photograph of your solutions. Your teacher will instruct you on how best to submit your work.
   
   
    
   
   
    
   Hemera/Thinkstock
   
   
2. It is your turn to create your own unique figure using all of the tangram pieces. Sketch the outline of your figure and show the solution using either Interactive Tangram or your paper pieces.
   
   Watch the “Tangram MathArt” video for a little inspiration.

Part B: At Play—Stained Glass Sailboat

 

Turn to page 184 in Mathworks 11. Read the introduction and complete “Stained Glass Sailboat” questions 1 to 4. Check with your teacher to see how you will share your results and compete with other students in question 4.

 

Part C: At Work—Trigonometry

 

Many trades use mathematics of the right triangle. Similar right triangles, the Pythagorean theorem, and right-triangle trigonometry are all part of the toolkit of carpenters, plumbers, electricians, surveyors, sheet metal workers, and many others. Have you ever wondered what mathematics these trades use?

 

Your goal for this part of the project is to research a trade that uses right-triangle mathematics. You might find the Internet, your textbook, or interviews with people in the trade some excellent sources of information. There are many examples in Mathworks 11, in the sections called “Math on the Job.”

1. Briefly describe how right-triangle mathematics is used in this trade.
   
   
2. Create two right-triangle situations that someone in this trade might encounter. At least one must require the use of two right-triangles. After describing each situation, provide complete solutions to each using trigonometry, the Pythagorean theorem, and/or similar triangles.

How You Will Be Evaluated

 

Your teacher will use the following rubric to evaluate your project. You can print or save a digital copy of the Project Rubric to complete your project self-assessment.

 

MODULE 4 PROJECT RUBRIC
Score	Required Concepts	Connections	Mathematical Calculations	Communication for Final Report
3 Exceeds Acceptable Standard	All of the project requirements have been addressed.	Explanations show a detailed understanding of the connections between the mathematics of the right triangle and their use in solving puzzles and problems in the trades.	All required mathematical representations are completed, correct, and support explanations.	The work is presented in a neat, clear, and organized fashion that is easy to read and/or see. Diagrams are used to support explanations.
2 Meets Acceptable Standard	Most of the project requirements have been addressed.	Explanations show an adequate understanding of the connections between the mathematics of the right triangle and their use in solving puzzles and problems in the trades.	There may be some minor math/calculation errors or flaws in reasoning.	The work is presented in an organized fashion but may be hard to read and/or see at times. Diagrams are included.
1 Below the Acceptable Standard	Few of the project requirements have been addressed.	The response shows little understanding of the connections between the mathematics of the right triangle and their use in solving puzzles and problems in the trades.	There are major math/calculation errors or serious flaws in reasoning.	The work appears sloppy and/or unorganized. It is hard to know what information goes together. Diagrams may not be used, or they are referred to inappropriately.
0 Does Not Meet the Minimum Standard	A minimal number of the project requirements have been addressed.	The response shows a lack of understanding of the connections between the mathematics of the right triangle and their use in solving puzzles and problems in the trades.	There is no understandable attempt at using mathematical representations.	There is not an understandable presentation of project work.
Total Score / 18	/3	/3 × 2 =  /6	/3 × 2 =  /6	/3