Lesson 5
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-3 SS |
| Book: | Lesson 5 |
| Printed by: | Guest user |
| Date: | Saturday, 13 September 2025, 3:14 AM |
Description
Created by IMSreader
1. Lesson 5
Module 4: The Right Kind Of Triangles
Lesson 5: Solving Problems Involving Two or More Right Triangles in Three Dimensions
Focus
© pzAxe/10589384/Fotolia
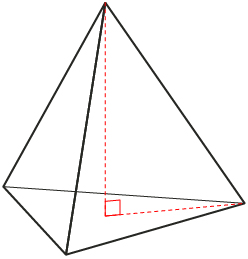
This three-dimensional pyramid took knowledge of trigonometry and the Pythagorean theorem to create. Can you see where the right triangles exist in this puzzle? They are not obvious because they are hidden inside the triangle. At what angle must the puzzle pieces be cut so that they fit together at the edges where the faces meet?
In Lesson 5 you will see other problems similar to this, where two or more right triangles will be needed to help find the solution.
In this lesson you will use your understanding of right triangles to solve problems involving two or more right triangles in three dimensions.
Lesson Question
In this lesson you will investigate the following question:
- How are three-dimensional problems solved using two or more right triangles?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from Try This and Share
- Lesson 5 Assignment (Save a copy of your lesson assignment to your course folder now.)
- the Project Connection
Materials and Equipment
- calculator
- tape measure or ruler
- protractor
- small open box, such as a shoe box
- stiff paper or cardstock (e.g., an old file folder)
- scissors
- markers
- a thin, straight rod about 40 cm long
1.1. Launch
Module 4: The Right Kind Of Triangles
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 5.
Launch will review the following topic:
- estimating angles
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.2. Are You Ready?
Module 4: The Right Kind Of Triangles
Are You Ready?
You are probably a good judge of length and distance, but how are you at estimating angles? Estimation skills are an important aspect of problem solving. You can use your estimation skills to evaluate whether or not an answer you determined is reasonable.
- Angle referents are simple tools found in everyday items that help you to estimate angle measures.
Take the square corner of a scrap piece of paper and fold the right angle in half. Then fold it in half again so that the three creases divide the right angle into quarters, as shown in the diagram. How large is each angle? Write the measures of these angles on the creases. These angles will serve as referents in judging angle size in question 2.
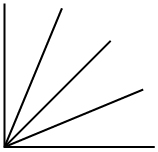
Answer
- Use the angles from question 1 as referents to estimate each angle.
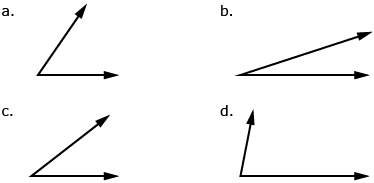
Answer
1.3. Refresher
Module 4: The Right Kind Of Triangles
Refresher
If you don’t know the answers in Are You Ready?, or if you require more information, review how to estimate angles.
Estimating Angles |
|
Go back to Are You Ready?, and try the questions again. Contact your teacher if you continue to have difficulty with the questions.
1.4. Discover
Module 4: The Right Kind Of Triangles
Discover
In this activity you will apply right-angle trigonometry to a problem in three dimensions. You will determine the angle a rod makes with the bottom of an open box. You need the following materials to complete this activity:
- small open box (a shoe box is ideal)
- ruler
- protractor
- thin rod that is too long to fit in the box
- stiff paper or cardstock (old file folders work well)
- scissors
- marker
- calculator
Step 1: Place one end of the rod in one corner of the box as shown in the picture. Measure the length of the rod found inside the box and remove it from the box. Also measure and record the inside dimensions (length, width, and height) of the box. Create a chart to organize your measurements.
Length of rod:
Length of box:
Width of box:
Height of box:
Step 2: Cut out and label a right triangle that will lie flat on the bottom of the box, as shown in the photograph. The legs of the triangle are the same as the width and length of the inside of the box. The hypotenuse of the triangle lies along the diagonal at the bottom of the box. Think of a way to determine the length of the hypotenuse of 
.
Step 3: Cut out and label a second triangle (ABD) so that the base of the new triangle is the same length as the hypotenuse (AB) of . The height of 
must match the height of the inside of the box. Fit vertically along the diagonal, as shown in the photograph. Think of a way to determine the length of the hypotenuse of .
Step 4: To determine the measure of ∠θ (the angle the rod makes with bottom of the box) answer the following questions.
Try This 1
- Without using a ruler, determine the length of AB, the hypotenuse of .
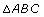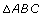is the triangle lying flat on the bottom of the box.
- You now know the lengths of two of the sides of . Which sides are they? What are their lengths?
- Use trigonometry to determine the measure of ∠θ. Use your protractor to check your answer. Are they the same?
Save a copy of your responses in your course folder.
Share 1
Share your responses to the questions in Try This 1 with a classmate or in a group.
How do the calculations you used in each step compare with others? Would you change any of the strategies or calculations you used?
If required, save a copy in your course folder of your discussion and the triangles you cut out.
1.5. Explore
Module 4: The Right Kind Of Triangles
Explore
In Discover you explored a problem setting involving three dimensions. In this section you will examine a variety of problems containing more than one right triangle in three dimensions.
Try This 2
The Muttart Conservatory in Edmonton is comprised of four square pyramids. The largest pyramid has a base length of 25.7 m and a vertical height of 24 m. Architects needed to determine the angle at which to cut the glass for the face at each edge of the pyramid.
Open Trigonometric Ratios to help visualize the problem in three dimensions. Answer the question posed in the segment.
iStockphoto/Thinkstock
Save a copy of your answer to your course folder.
Share 2
Share your response to the question in Try This 2 with a classmate or in a group. Then draw two right triangles that help determine the angle at the edges of the pyramid.
If required, save a copy of your discussion and the triangles you drew in your course folder.
1.6. Explore 2
Module 4: The Right Kind Of Triangles
Now you will work through an example similar to the problem you encountered Try This 2. The example may help you with any difficulties you had in Try This 2.
Example
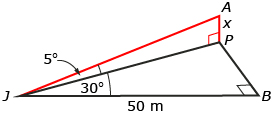
Jasmine is 50 m from an intersection with a straight road. Down the road is a power pole. Jasmine must turn to her left through an angle of 30° to measure angle of elevation of the top of the pole. If the angle of elevation of the top of the pole is 5°, to the nearest tenth of a metre, how high is the pole?
Read through the following written solution, or watch the video solution, titled Jasmine’s Angle of Elevation.
Video Solution
© Okea/12953148/Fotolia
Written Solution
Determine the length of JP, Jasmine’s distance from the pole.
Using triangle JPB,
From SOH-CAH-TOA, use the cosine ratio. |
 |
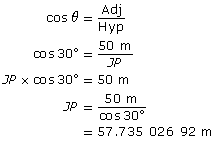Use triangle AJP to find the height of the pole.
From SOH-CAH-TOA, use the tangent ratio.
The pole is approximately 5.1 m tall. |
 |
1.7. Explore 3
Module 4: The Right Kind Of Triangles
Example
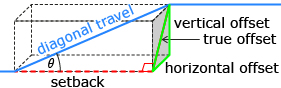
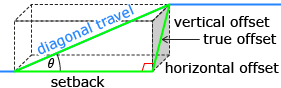
Plumbers must occasionally make use of a rolling offset to avoid obstacles when installing pipes. A rolling offset is when a pipe is shifted horizontally (left or right) and vertically (up or down). You can picture a rolling offset by thinking back to your work with the box in Discover. In the diagram, the pipe enters one corner at the bottom of the box and leaves by travelling diagonally to the opposite upper corner.
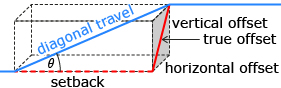
- For a vertical offset of 12 in and a horizontal offset of 9 in, what is the true offset? The true offset is the diagonal distance across the shaded end of the box.
- A complication in determining a rolling offset is that the diagonal travel uses a separate piece of pipe that must be joined to the horizontal sections. The fittings come in certain angles only. The fitting angle in the diagram, marked θ, is the angle between the diagonal travel (blue pipe) and the setback (dotted red horizontal line). If 22.5° fittings must be used, determine the setback. Round to the nearest hundredth of an inch.
- Determine the length of the diagonal travel. Round to the nearest hundredth of an inch.
Solution
|
 |
|
 |
|
 |
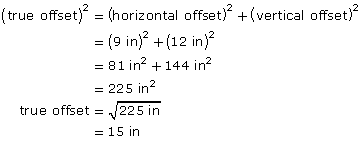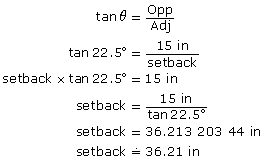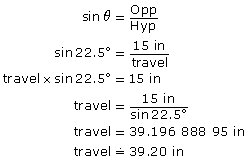For another example, turn to page 191 of MathWorks 11. Work through “Example 3.”
Self-Check 1
- Gustav was standing on the balcony of a high-rise building, 50 m above the street below. He measured the angle of depression of a pedestrian on the street to be 76°. Gustav sketched a diagram and calculated the distance the pedestrian was from the point on the street directly below the balcony. His answer was approximately 200.5 m. Is Gustav’s answer reasonable? Why or why not? Support your answer with a diagram.
Answer
1.8. Connect
Module 4: The Right Kind Of Triangles
Connect
Going Beyond
iStockphoto/Thinkstock
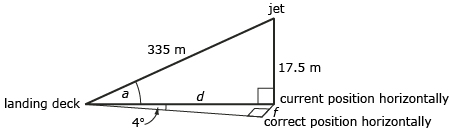
The goal of a military jet pilot is to snag the tailhook (the hook on the bottom of the plane) on the third of four wires on an aircraft carrier landing deck. To do this requires precision in approaching the landing deck at the correct angle. This angle is communicated to the pilot by coloured lights on the Optical Landing System. The goal is to see an amber light (called the “meatball”) in line with a string of green lights. Suppose a pilot is coming in for a landing with the lights lined up correctly. The jet is 335 m away from the edge of the landing deck and 17.5 m above the deck of the aircraft carrier (vertical distance). The information is summarized in the following diagram.
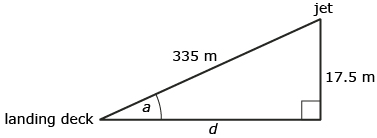
- Determine how far horizontally, d, the plane is from the aircraft carrier. Round to the nearest metre.
- In addition to coming in on the right angle vertically, the plane also must line up horizontally (to the left and right) so that it can snag the wire efficiently. This is also communicated to the pilots through lights. Suppose the pilot sees a slow, flashing red light indicating that he or she is 4° to the right of centre. How many metres to the right is the plane off centre (find side f )? Round to the nearest metre.
Project Connection
You are now ready to complete Part C: At Work—Trigonometry of the Module 4 Project.
Remember to save all your work to your course folder to submit at the end of the module.
Lesson 5 Assignment
Your lesson assignment contains some problems for you to solve using knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies that you have learned to a new situation.
Open your Lesson 5 Assignment that you saved to your course folder and complete the questions. Please show your work to support your answers.
1.9. Lesson 5 Summary
Module 4: The Right Kind Of Triangles
Lesson 5 Summary
The National Film Board’s 1965 film High Steel celebrates the skill and bravery of the steel workers from the Kahnawake Reserve near Montreal. For decades, people from this community worked on the steel structures that give New York its skyline.
Search the Internet for “National Film Board of Canada High Steel,” and watch the video.
Iron workers, whether erecting bridges or buildings, depend on the design of these structures for their safety. These designs are, in part, an application of the mathematics you studied in this lesson.
In this lesson you investigated practical applications of right–angle trigonometry and the Pythagorean theorem. These applications involved more than one right triangle in three dimensions.