Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-3 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Tuesday, 2 December 2025, 7:01 AM |
Description
Created by IMSreader
1. Lesson 2
Module 6: Surface Area
Lesson 2: Estimating Surface Area
Focus
Solar panels are becoming increasingly common for both urban and rural use. The cells in the panels convert light from the sun into electrical energy. The amount of electricity produced depends on the surface area covered by the panels. Solar energy technicians help design and install systems like the ones shown in the photos. What area would you estimate each panel covers? A square metre? Less? More? Are there objects in the pictures you could use to help with your estimate? In this lesson, you will refine your skills in estimating surface area.

both photos: iStockphoto/Thinkstock
Lesson Questions
- How are different strategies used to estimate surface area?
- How can a referent be used to estimate surface area?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from Try This and Share
- your contribution to the Mathematics 20-3: Glossary Terms and Formula Sheet
- Lesson 2 Assignment (Save a copy of your lesson assignment to your course folder now.)
- the Project Connection
Materials and Equipment
- an old newspaper
- scissors
- tape
- rulers (SI and imperial)
- calculator
- 1-cm Grid Paper
Time
This lesson has been designed to take 150 minutes; however, it may take more or less time depending on how well you are able to understand the lesson concepts. It is important that you progress at your own pace based on your own learning needs.
1.1. Launch
Module 6: Surface Area
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 2.
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.2. Are You Ready?
Module 6: Surface Area
Are You Ready?
In Module 3, and in previous mathematics courses, you converted among different area units in both the SI and imperial systems.
- How many square inches are there in a square foot?
Answer
- Jillian's room is rectangular and measures 9 ft by 12 ft. Her room was just carpeted. How many square yards of carpet were needed? Answer
- How many square millimetres are there in a square centimetre? Answer
-
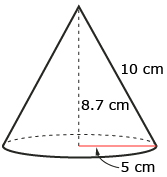
- Determine the surface area of the following cone. Round to the nearest square centimetre.
Answer
If you answered the Are You Ready? questions without problems, move on to Discover.
If you found the Are You Ready? questions to be difficult, complete Refresher to review these topics.
1.3. Refresher
Module 6: Surface Area
Refresher
If you don’t know the answers in Are You Ready?, or if you require more information, work through the following activities to review unit conversions, rounding, and finding the surface area of a cone.
Go back to Are You Ready? and try the questions again. Contact your teacher if you continue to having difficulty with the questions.
1.4. Discover
Module 6: Surface Area
Discover
Before you can accurately estimate surface area, it is critical that you have a mental image of the more common area units in both the SI and imperial systems. To help you visualize the size of these units, complete the following activity.
Try This 1

Jupiterimages/ Creatas/Thinkstock
You will need the following:
- one or two old newspapers
- tape
- scissors
- measuring tape
- ruler with both SI and imperial units
Step 1: Begin by taking pages from an old newspaper. Lay them out to form a square measuring 1 m on each side. Tape the pages together. The square is 1 m2 in area.
Are there any items around you, such as a window or a cupboard, that match the size of this area? Record at least three items in a chart like the one that follows.
Step 2: Using another piece of newspaper, measure and cut out a small square that measures 1 cm on each side. The square is 1 cm2 in area.
Are there any items around you that match the size of this area? Record at least three items in the chart.
Step 3: Repeat Steps 1 and 2 for squares measuring 1 yd2 (1 yd by 1 yd), 1 ft2 (1 ft by 1 ft), and 1 in2 (1 in by 1 in) in area.
Based on what you found, answer the following questions.
- The term referent refers to the items you found that were about the same size as the newspaper squares you created. A referent is the mental image you “see” or “refer to” when you work with the various area units such as 1 m2 or 1 ft2.
Fill in the chart with the referents that you found in Steps 1, 2, and 3.
Area Unit Referent 1 Referent 2 Referent 3 1 m2 1 cm2 1 yd2 1 ft2 1 in2
- A skill that is useful with respect to the trades is being able to convert between area units. Using the squares that you created from newspaper, determine the conversion factor between the following units.
- 1 m2 = ______ cm2
- 1 yd2 = ______ ft2
- 1 ft2 = ______ in2
- 1 yd2 = ______ in2
- 1 m2 = ______ ft2
- 1 m2 = ______ yd2
![]() Save your work in your course folder.
Save your work in your course folder.
Share 1
Share your responses to the questions in Try This 1 with a classmate or in a group.
- Share your lists of referents to create a larger, combined list.
- Confirm your conversion factors with your partner or your group and by using the Internet.
![]() If required, save a copy of your discussion in your course folder.
If required, save a copy of your discussion in your course folder.
1.5. Explore
Module 6: Surface Area
Explore
In Discover, you examined various referents for some common units for area. In this section you will use these referents and other strategies, like rounding and using grid paper, to estimate the surface area of three-dimensional objects. Creating a net can be extremely helpful for all strategies.
Try This 2

Hemera Technologies/AbleStock.com/Thinkstock
One method of estimating surface area is drawing the net of the three-dimensional object on grid paper.
- Trace a net of a toonie on 1-cm Grid Paper. Don’t forget to include the edge of the toonie—it is actually a short cylinder.
- Look at the net you drew, and count the number of square centimetres it covers to estimate the surface area of the toonie.
- Use a ruler to measure the diameter and height of the toonie. Check to see how close your estimate is to the actual surface area by using the surface area of a cylinder formula,
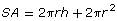 .
.
- What referent could you have used to estimate the surface area of the toonie? How close to the answer in question 3 do you think this estimate would have been?
Share 2
- Explain why both the values found in questions 2 and 3 could be considered estimates of the surface area of a toonie?
- Would square-inch or square-centimetre graph paper help to provide a more accurate estimate of the toonie’s surface area? Explain.
1.6. Explore 2
Module 6: Surface Area

Jack Hollingsworth/ Photodisc/Thinkstock
In Try This 2 you estimated the size of the toonie three different ways—using grid paper, using a referent, and taking rough measurements. In the next example you will see how Jenn used a referent to estimate the surface area of her front door.
Example 1
Jenn used her referent of a square metre (1 m2) to estimate the total surface area of the front door in her home. She made sure to measure all six surfaces (the front, the back, and the four edges) to get the best estimation possible.
She estimated the surface area of the door to be about 4 m2.
Jenn then decided to check her estimation skills. She took careful measurements with a measuring tape and drew a net to record the measurements. She then calculated the door’s surface area in order to see how close her estimate was to the actual area.
Jenn’s door measured 0.91 m wide, 2.03 m tall, and 4.5 cm or 0.045 m thick. Her sketch of the net of the door looked like this.
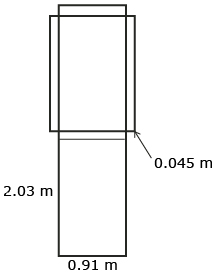
Jenn then calculated the surface area of the door using the steps below.
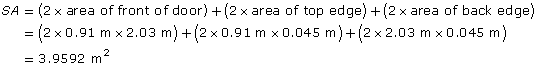
Jenn was happy to see that her estimate of 4 m2 is very close to the actual area.
In the last example, Jenn used a referent to do her estimation of the surface area of the door. In the next example, referents and rounding are both used in the estimation.
1.7. Explore 3
Module 6: Surface Area
Example 2
A roofer needs to estimate the number of bundles of shingles he must order to cover the roof in the illustration. A bundle of shingles covers 100 ft2. The roofer knows from experience that he should overestimate by adding another 4% to account for waste, as well as extra shingles needed for the first rows and the ridges, hips, and valleys on the roof. On bare or new roofs, carpenters can use a standard sheet of plywood as their referent. A standard sheet of plywood is a rectangle measuring 4 ft wide and 8 ft long. It covers an area of 4 ft × 8 ft or 32 ft2.
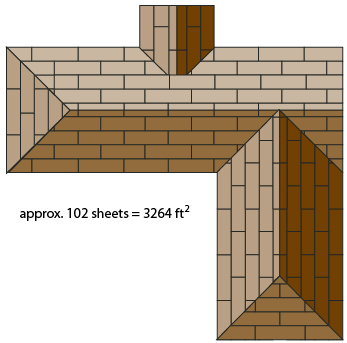
The image to the left shows the bare roof with the standard sheets of plywood exposed. The roof is covered by approximately 102 sheets of plywood. How many bundles of shingles will the roofer need to cover the roof in the illustration?
Solution
From the ground, the roofer counts the number of sheets of plywood on the roof. His count is approximately 102 sheets.
![]()
To account for waste, as well as the extra amount needed, the roofer adds on 4%.
![]()
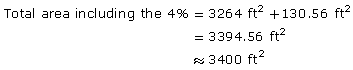
If each bundle covers approximately 100 ft2, the roofer will order 34 bundles, since 34 × 100 ft2 = 3400 ft2.
Self-Check 1
- Marty works as a groundskeeper at a local golf course. Marty’s supervisor has asked him to apply fertilizer to the green on the twelfth hole. Marty must estimate the area of the green before he applies the fertilizer. He knows the green is almost a perfect circle. Marty also knows that one pace is approximately one yard. How can he estimate the area of the green?
Answer

iStockphoto/Thinkstock
-
Do question 6 on page 126 of MathWorks 11. Answer
-
Farmers use conical grain-pile covers to protect grain stored in the field. Estimate the area of a cover needed to protect a conical pile of wheat 99 ft in diameter with a slant height of 103 ft. Answer

Photo courtesy of Inland Tarp & Liner, Inc.
It is now time to add new math terms to Mathematics 20-3: Glossary Terms.
In this lesson the new term you will add is
- referent
1.8. Connect
Module 6: Surface Area
Connect
Going Beyond

iStockphoto/Thinkstock
Compare the hands in the photograph. Which hand has the greatest surface area?
A person's total surface area depends on his or her height and weight. And, a person’s metabolism can be predicted by knowing the surface area of his or her body. Pharmacists and doctors calculate body surface area in order to determine appropriate dosages to give patients.
The Cross Cancer Institute in Edmonton uses the Mosteller formula to estimate Body Surface Area (BSA).
![]()
- Use the Mosteller formula to find the BSA of a woman who is 150 cm tall and weighs 55 kg.
- What is your BSA?
Lesson 2 Assignment
Your lesson assignment contains some problems for you to solve using the knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies that you have learned to a new situation. Show your work to support the answers.
Open the Lesson 2 Assignment that you saved to your course folder and complete the questions.
1.9. Lesson 2 Summary
Module 6: Surface Area
Lesson 2 Summary

Jupiterimages/Pixland/Thinkstock
Fashion is a global multi-billion dollar industry. Clothes are often designed in one country, manufactured in another, with the fabrics obtained from a third country, and then sold around the world! Two input costs of a dress, such as the one in the photo, are the quality and the amount of fabric. Could you estimate the amount of fabric used to make this dress?
As you have seen in this lesson, being able to estimate area is an important skill in a wide spectrum of careers. You explored estimating surface area by using referents.