Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-3 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Saturday, 1 November 2025, 4:32 AM |
Description
Created by IMSreader
1. Lesson 3
Module 2: Number
Lesson 3: Puzzles
Focus

iStockphoto/Thinkstock
Have you ever noticed how two people can be playing the same game but have completely different strategies? Understanding strategy can help to improve your success with one-player games and puzzles.
You are often faced with problem solving in your life; developing and evaluating strategies for how to meet your goals is a necessary skill. Playing games or simulations are an opportunity to think about and practise using strategies. In the previous lessons, you evaluated information to help make decisions about businesses and vehicles. The steps to help you make your decision are part of the strategy in making those financial decisions. The skills used to understand strategy in puzzles and games are similar.
In this lesson you will learn and practise strategies for solving puzzles and logic games.
Lesson Outcomes
At the end of this lesson you will be able to
- solve puzzles and logic games, and explain the strategy used
- identify errors in solutions to puzzles and logic games
Lesson Question
You will investigate the following question:
- How can you use problem-solving strategies to solve puzzles and logic games?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 3 Assignment (Download the Lesson 3 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms
- work under Project Connection
1.1. Discover
Module 2: Number
Discover
At first glance, it may seem like the strategies appropriate for solving puzzles will be unique to each type of puzzle. However, it turns out that there are a number of strategies that can be used for many different types of puzzles.
Try This 1
Try to solve the following puzzles. You may find it helpful to work with a partner.
-
Gears

A home-made grandfather clock has five gears connected vertically. If the first (top) gear rotates in a clockwise direction, in which direction does the fifth (bottom) gear rotate? -
Chickens and Pigs
Andy and Kai went out to a farm on Saturday where they saw chickens and pigs. Andy said that he counted 14 animals altogether. Kai said she counted 48 legs. How many chickens were there, and how many pigs were there?
iStockphoto/Thinkstock
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
Share your solution strategies (or attempts if you were not successful) with a partner. How were your strategies similar? How were they different?
![]() If required, place a summary of your discussion in your course folder.
If required, place a summary of your discussion in your course folder.
1.2. Explore
Module 2: Number
Explore
The strategies you used to solve the puzzles in Try This 1 may have been unique to you, or they may have been similar to your partner’s strategies. Here are some possible first steps for each of the puzzles in Try This 1.
1. Gears |
2. Chickens and Pigs |

|

|
In each case, a picture was drawn as a starting point. This is a very common tool for solving problems of all types, including puzzles.
Self-Check 1
- Use the picture above to solve the Gears problem from Try This 1. Answer
- Use the picture above to solve the Chickens and Pigs problem from Try This 1. Answer
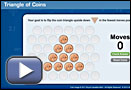
- Open Triangle of Coins and solve the puzzle. Answer
-
Solve this Blocks of Wood puzzle.

iStockphoto/Thinkstock
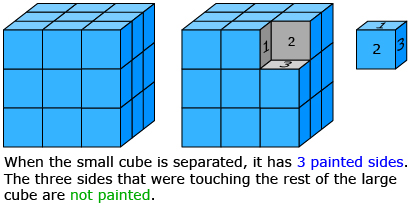
Suppose you took a 3 inch × 3 inch × 3 inch cube made from joining 27 small cubes and dipped the cube in a can of paint. Each of these smaller cubes will have paint on 3, 2, 1, or 0 sides. How many cubes will have paint on 3, 2, 1, and 0 sides? Answer
Answer
-
A famous logic puzzle is called Prisoners and Hats. There are many different versions available. Here is one version. Solve the puzzle.

Three men are standing in a row, all facing the same direction. The man in the back can see the two men in front of him. The man in the middle can only see the man in front of him. The man in front cannot see either of the other two men.
A hat is placed on the head of each man. There were three blue hats and two red hats to choose from, so two hats are left over.
Each man cannot see the colour of the hat on his head, or the colours of the two leftover hats. They all know how many hats there were to start with, and they are told that any man who can determine the colour of the hat on his own head will win a prize.
The man at the back said he didn’t know the colour of his hat. The man in the middle said he didn’t know the colour of his hat. The man in front said he knew the colour of his hat and he was correct.
What colour was the hat of the man in front, and how did he know?
You may want to draw pictures and try out different combinations.


Answer
1.3. Explore 2
Module 2: Number
Drawing pictures is just one of many techniques for solving problems. Try the problems below to experience another strategy for solving problems.
Try This 2
Try solving the following problems.
- Time to Midnight
John looked at a clock and commented that in two hours it would be half as long until midnight as it would be if it were an hour later. What time is it?

iStockphoto/Thinkstock - Sports Kids Puzzle
The young girls in this puzzle are Diane, Jackie, and Sarah. The young boys are Chuck and Harry.
From the clues provided, determine what
- sport each young person plays: baseball, basketball, soccer, swimming, volleyball
- town they are from: Calgary, Edmonton, Red Deer, Sherwood Park, St. Albert
- their father does for a living: baker, carpenter, mechanic, real-estate agent, teacher
Clue 1: The soccer player’s father is a real-estate agent. The mechanic is the father of neither Harry nor the baseball player.
Clue 2: The teacher’s daughter from Red Deer is neither Jackie nor the swimmer.
Clue 3: Diane is playing division 1 volleyball. Sarah’s father is not the mechanic.
Clue 4: The basketball player lives in St. Albert.
Clue 5: Chuck's father is a baker who neither lives nor works in Sherwood Park.
Clue 6: Sarah, who lives in Calgary, is not a baseball player.
Clue 7: Harry has no interest in swimming or basketball.
Clue 8: The retired carpenter and his daughter drove to a competition in Edmonton, where one of the other players lives.
Clue 9: Chuck was scheduled to play an away game in Red Deer but the game was rained out.
Clue 10: Sarah is the only athlete who does not compete as part of a team.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
Share your solution strategies (or attempts if you were not successful) with a partner.
- How were your strategies similar? How were they different?
- Were all of your strategies successful?
- Which strategy would you try the next time you solved a puzzle like this?
![]() If required, place a summary of your discussion in your course folder.
If required, place a summary of your discussion in your course folder.
1.4. Explore 3
Module 2: Number
The strategies you used to solve the puzzles in Try This 2 may have been unique to you, or they may have been similar to your partner’s strategies. For these problems, it would be very helpful to use tables to organize your solutions. In the following Self-Check, tables have been suggested to help you solve the problems.
Self-Check 2
- Time to Midnight
Try using the following table to organize your thinking and solve the puzzle from Try This 2.
Current Time
Time to Midnight 2 h Later
Time to Midnight 1 h Later
Answer - Sport Kids Puzzle
Solve the puzzle from Try This 2 by creating the following table.
Diane
Jackie
Sarah
Chuck
Harry
Sport
Profession
Location
Answer - Husbands and Wives
Mary is a blonde, Kanisa is a redhead, and Sharinder is a brunette. They are married to Alex, François, and Kobi but
- Sharinder does not like Kobi
- Kanisa is married to Kobi’s brother
- Alex is married to Kanisa’s friend
Who is married to whom?
Answer
1.5. Explore 4
Module 2: Number
The previous problems have highlighted a number of strategies for solving puzzles:
Strategy |
Example Problems |
Draw a picture |
|
Create a table to organize information |
|
Logic |
|
Note that logical reasoning was used in all of the puzzles. The logical reasoning you used was the process of drawing conclusions based on the information given. When solving puzzles you may use a variety of strategies that use logical reasoning.
Following are some strategies that may be useful:
- looking for patterns
- guessing and checking
- eliminating possibilities
- working backwards
- simplifying or rewording the original problem
In the next Self-Check you will have a chance to use logical reasoning to solve a puzzle game.
Self-Check 3

iStockphoto/Thinkstock
Sudoku is a popular puzzle game where a player completes a given, partially completed, 9 by 9 grid by filling in the missing numbers. The 9 by 9 grid is broken into smaller 3 by 3 regions. Each row, column, and region contains nine cells each. The numbers 1 to 9 are filled in to complete the puzzle. The rules for Sudoku are as follows:
- Each row of the 9 by 9 grid contains the numbers 1 through 9 only once.
- Each column of the 9 by 9 grid contains the numbers 1 through 9 only once.
- Each 3 by 3 smaller grid contains the numbers 1 through 9 only once.
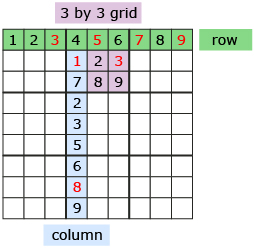
![]()
-
Search the Internet for a Sudoku game (use the keywords “wolfram sudoku demo” as your search term). Open the game and set the difficulty to a low number, such as 20, and try to complete the puzzle and check your answers. Once you have solved that puzzle, increase the difficulty and try again.
- Explain and verify a strategy you used to solve the Sudoku game. Answer
1.6. Explore 5
Module 2: Number
Often when solving a puzzle, you will make a mistake. The mistake may show itself as you continue to solve the puzzle. In Try This 3, you will try to determine where a mistake occurred in a solution.
Try This 3
A nonogram is a puzzle where you try to shade in the correct spaces in a grid to reveal a picture. The numbers on the outside of the grid tell you how many blocks there are in each row or column, and how these are grouped.

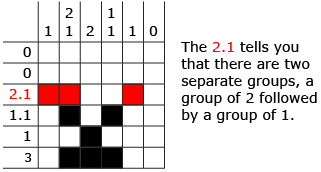

Faiza is going to solve the nonogram shown.
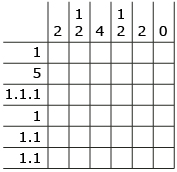
She begins to complete the puzzle, as shown, using an x in boxes she knows cannot be filled. In step 6, she realizes that it is impossible to use the clue 1.1.1 because she has already concluded that the red box cannot be used.
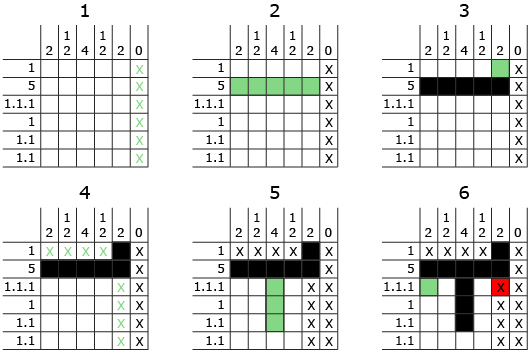
- Follow Faiza’s steps and determine in which step her error occurred. Explain how you know an error occurred.
- Complete the puzzle correctly.
- Describe how you could make your own nonogram puzzle for another student to complete.
![]() Save your responses in your course folder.
Save your responses in your course folder.
In Try This 3, an error occurred in step 3. Faiza did not have enough information to conclude that the square should be filled in. When solving puzzles of this type, it is important to be entirely sure before filling in a box with a square or an x.
1.7. Connect
Module 2: Number
Complete the Lesson 3 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are now ready to complete the rest of Module 2 Project: Owning and Operating a Small Business. Go to the Module 2 Project, and complete Part 3 and Part 4.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.8. Lesson 3 Summary
Module 2: Number
Lesson 3 Summary

Zoonar/Thinkstock
In this lesson, you explored strategies that can be used to solve puzzles. You were asked to explain the strategy you used. One strategy was drawing a picture to help understand and solve a puzzle. Another strategy was to use a table to help organize information to solve the puzzle. Throughout the lesson you used logical reasoning and practised solving different types of puzzles.
You may have found some of the following strategies useful:
- drawing a picture
- looking for patterns
- guessing and checking
- making a list
- eliminating possibilities
- working backwards
- simplifying or rewording the original problem