Lesson 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-3 SS |
| Book: | Lesson 1 |
| Printed by: | Guest user |
| Date: | Sunday, 2 November 2025, 9:00 PM |
Description
Created by IMSreader
1. Lesson 1
Module 5: Geometry
Lesson 1: Triangles
Focus
Take a look around and you will notice that triangles are everywhere! Watch the video “Exploring and Solving Triangles.”

iStockphoto/Thinkstock
Triangles can be found in many structures, including bridges, frameworks of buildings, scaffolding, roof trusses, and playground swings.
Can you think of other structures that use triangles within their designs? Why are triangles commonly used? Are triangles used for aesthetics, structural support, or both?
As a carpenter, steelworker, or any other tradesperson working on a structure such as the one shown, it is important to understand the properties of triangles. Triangles are not only incorporated into a structure’s design for visual appeal, but also for the strengthening of the structure.
Lesson Outcomes
At the end of this lesson you will be able to
- solve problems that involve triangles
Lesson Question
You will investigate the following question:
- How can the properties of triangles be used to help solve problems?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 1 Assignment (Download the Lesson 1 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
- work under Project Connection
Self-Check activities are for your own use. You can compare your answers to the suggested answers to see if you are on track. If you have difficulty with concepts or calculations, contact your teacher.
Remember that the questions and activities you will encounter provide you with the practice and feedback you need to successfully complete this course. You should complete all questions and place your responses in your course folder. Your teacher may wish to view your work to check on your progress and to see if you need help.
Materials and Equipment
- calculator
1.1. Launch
Module 5: Geometry
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson you should be able to
- define polygon
- solve for the missing angles in a triangle
- solve for the lengths of sides of a right-angled triangle using the Pythagorean theorem
1.2. Are You Ready?
Module 5: Geometry
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Define the term polygon. Answer
- Calculate the missing angle measures.
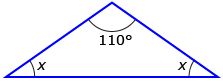
- Use the Pythagorean theorem, a2 + b2 = c2, to calculate the value of the missing side length.
- Calculate the unknown angle measure, y, and the unknown side, x.
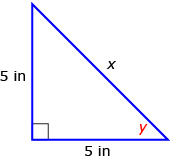
Answer
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 5: Geometry
Refresher
Open "Polygon" and review the definition and naming of polygons, and explore polygons further using the demonstration applet.
To review angles in a triangle, open the “Exploring Angles Within a Triangle” interactive and answer the following questions.
- Create a scalene triangle in which all three angles are different. What is the sum of all the angles?
- Create an isosceles triangle in which two of the three angles are the same. What is the sum of all the angles?
- Create an equilateral triangle in which all three angles are the same. What is the sum of all the angles?
- What is the sum of the angles in any triangle?
Recall that the triangle sum theorem states that the sum of the interior angles of any triangle is equal to 180°.
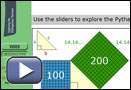
To see the importance of the Pythagorean theorem in the structural design of buildings, watch the “Exploring the Pythagorean Theorem” video.
To review the Pythagorean theorem, open the “Exploring the Pythagorean Theorem” interactive and explore the activity by changing the a and b values and see how the c value for the right-angled triangle is calculated.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 5: Geometry
Discover

Hemera/Thinkstock
Suppose you are a skilled carpenter, and you have been asked to construct a gazebo similar to the one shown. As you can see, there are a number of different shapes involved in the design of this structure, in particular, triangles. How will you determine the lengths and angles of each piece that needs to be cut, such that the pieces fit nicely together?
Complete the following Try This activity to develop your understanding of different types of triangles.
Try This 1
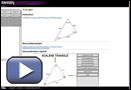
Open the Triangle Demonstration Applet and analyze the constructed triangle after following the instructions. Record your findings after each set of instructions.
- Click and drag the top corner of the triangle until all the angles are equal and the side lengths are equal. Look above the triangle. What kind of triangle is this?
- Now click and drag the top corner of the triangle to the side of the screen. Look above the triangle. What kind of triangle is this?
- Now click and drag the top corner of the triangle to make one angle in the triangle a right angle (90°). Look above the triangle. What kind of triangle is this?
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or in a group, share your responses to Try This 1 and address the following additional questions:
- What characteristics classify a triangle as right, scalene, isosceles, or equilateral?
- What characteristics classify a triangle as acute or obtuse?
- Can a triangle be classified by its sides as well as its angles? Explain, and provide examples if possible.
- Is it possible to change the length of one side of the triangle without affecting other parts of the triangles (sides and angles)?
![]() If required, place a summary of your discussion in your course folder.
If required, place a summary of your discussion in your course folder.
1.5. Explore
Module 5: Geometry
Explore
As you are aware, a triangle is a polygon made up of three sides. It is a very popular shape that is used in many structures for both aesthetics and its incredible strength.
The triangle is the strongest of all polygons since the length of each side is dependent on the other two sides, and the measurement of each angle within the triangle is dependent on the other two angle measurements. As you learned in the Try This 1 activity, you cannot change one measurement—be it the length of the side or angle measurement—without affecting the other measurements. The angles and sides act as reinforcements for one another, making the triangle very rigid and strong, hence the reason it is so popular in construction!
Triangles can be classified in two different ways—by angle measure and by side length.
| Triangles Classified By Angle Measure | ||
| acute | all three angle measures are less than 90° |  |
| obtuse | one angle measure is greater than 90° | |
| right | one angle measure is 90° |  |
Source: MathWorks 12 Student Book/Teacher Guide. (Vancouver: Pacific Educational Press, 2011.)
| Triangles Classified By Side Length | ||
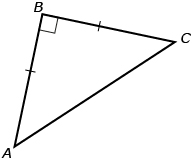
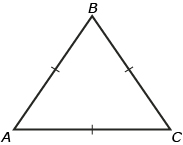
| equilateral | three sides are of equal length and three angles are of equal measure |  |
| isosceles | two sides are of equal length and two angles are of equal measure | 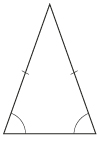 |
| scalene | no sides are of equal length and no angles are of equal measure |  |
Source: MathWorks 12 Student Book/Teacher Guide. (Vancouver: Pacific Educational Press, 2011.)
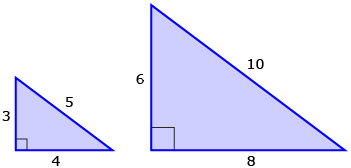
The 3:4:5 triangle is a right-angled triangle where the sides have a ratio of 3:4:5. The image shows some examples of 3:4:5 triangles, also known as Pythagorean triples.
The 3:4:5 triangle has been used for centuries, and it is claimed to be the special triangle used to construct the Great Pyramids of Giza.

iStockphoto/Thinkstock
It appears the Egyptians were familiar with some mathematics that are still used today by carpenters and other tradespeople to square corners when a measuring device is not available. For example, a carpet installer may use the 3:4:5 triangle rule to ensure that the corners of a carpet that have been cut are indeed 90 degrees.
1.6. Explore 2
Module 5: Geometry
In the next Try This, you will discover how properties of triangles can be used to determine the angles of triangles.

iStockphoto/Thinkstock
Try This 2
A construction worker builds triangular roof trusses. She needs to know the side lengths and interior angles of the trusses that have been built.
- Four triangular roof trusses have been built and are drawn in the following table. Complete the table using your knowledge of triangles.
Triangle
Classify by Angle (acute, obtuse, or right)
Classify by Side Length (equilateral, isosceles, or scalene)
Measure of Indicated Angles
∠A =
∠B =
∠C =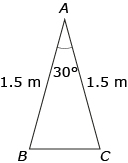
∠B =
∠C =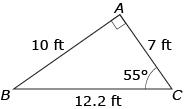
∠B =
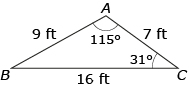
∠B =
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.7. Explore 3
Module 5: Geometry
In Try This 2, you may have noticed the following point.
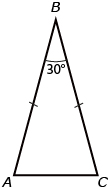
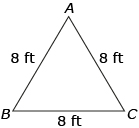
In an equilateral triangle all three angles are equal, so the measure of each angle would be 180° ÷ 3 = 60°.
In the diagram,
∠A = 60°, ∠B = 60°, ∠C = 60°
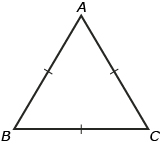
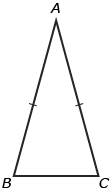
In an isosceles triangle, the interior angles opposite the equal sides are equal. In the diagram,
∠B = ∠C
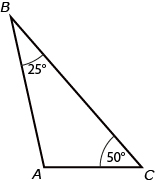
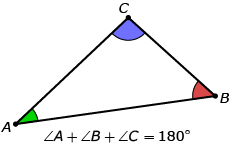
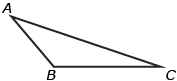
In a scalene triangle, as with all triangles, the three interior angles must add up to 180 degrees. If you know two of the angles, the third angle can be determined by subtracting the two known angles from 180. In the diagram,
∠A + ∠B + ∠C = 180°
Read “Example 1” on page 182 of the textbook. As you read, notice how the unknown angles in each triangle are calculated.
Self-Check 1
- Answer “Build Your Skills” question 1 on page 187 of the textbook. Answer
- Answer “Build Your Skills” question 5 on page 189 of the textbook. Answer
- In each of the following triangles, solve for the missing angles and classify each triangle as
- scalene, isosceles, or equilateral
- acute, obtuse, or right
1.8. Explore 4
Module 5: Geometry
You have determined how triangles can be classified and how angles can be calculated.
In the next Try This, you will explore how unknown side lengths of right triangles can be determined.
Try This 3
The following is a simple diagram of the infield of a baseball diamond. The baselines are drawn from home plate to first base, from first base to second base, from second base to third base, and from third base to home plate.


Huntstock/Thinkstock
The distance between each of the three bases and home plate is 90 ft. All angles formed by the baselines are right angles.
- Imagine the catcher (at home plate) has to throw the baseball to second base.
- What type of triangle is formed when the vertices are home plate, first base, and second base?
- How far is it from home plate to second base?

- If the shortstop is placed somewhere between second base and third base, describe the location of this player in order to form each of the following triangles:

- an acute triangle with the shortstop, third base, and home plate as the vertices
- an obtuse triangle with the shortstop, third base, and home plate as the vertices
- a right triangle with the shortstop, third base, and home plate as the vertices
- A base runner is 30 ft from second base on her way to third base.
- How far is she from home plate in a straight-line distance?
- How far is she from home plate if she continues to run the bases?
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.9. Explore 5
Module 5: Geometry
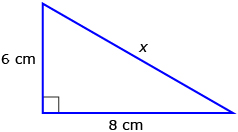
In Try This 3, you may have been able to determine the lengths of the sides of the right triangle that was formed by using the Pythagorean theorem: a2 + b2 = c2.
View Calculating Distances Using Right Triangles to see how you could determine distances using right triangles.
To see another example of how to calculate distances using right triangles, read “Example 2” on page 184 of the textbook. As you read, notice that when there is a right triangle within the problem, the Pythagorean theorem can be used to determine the length of any side of the right triangle.
Self-Check 2
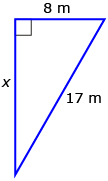
- Firefighters, construction workers, and many others rely on the use of ladders in their lines of work. For example, the height to a second-storey building is 20 ft, and a construction worker needs to put the ladder 5 ft away from the building to make the ladder safe. What is the minimum length the ladder needs to be in order to reach the top of the building? Answer

iStockphoto/Thinkstock
Hemera/Thinkstock
-
The length of a ramp used to load and unload trucks is 20 ft. The horizontal distance along the ground from the bottom edge of the ramp to the truck is 19.75 ft. How high is the truck? Answer
-
Answer “Build Your Skills” questions 3 and 6 on pages 188 and 189 of the textbook. Answer
Add the following terms to your copy of Glossary Terms:
- equilateral triangle
- isosceles triangle
- scalene triangle
- acute triangle
- obtuse triangle
- right triangle
Add the following formula to your copy of Formula Sheet:
- Pythagorean theorem: a2 + b2 = c2
1.10. Connect
Module 5: Geometry
Complete the Lesson 1 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
Go to the Module 5 Project: Designing a Yard and read over all project requirements. Become familiar with what you will be doing and how you will be assessed.
Your Module 5 Project will be evaluated by your teacher using the evaluation guidelines in the Project Rubric. Read the rubric carefully. Make sure you are aware of how you will be assessed. You can print or save a digital copy of the rubric.
1.11. Lesson 1 Summary
Module 5: Geometry
Lesson 1 Summary

Top Photo Group/Thinkstock
In this lesson, you classified triangles according to side length and angle measure. Terms such as equilateral, isosceles, scalene, acute, obtuse, and right are associated with the classification of triangles. Applying the Pythagorean theorem has been useful in this lesson to help determine the side lengths of right triangles.
In the next lesson, quadrilaterals will be examined. Some of the topics in this lesson about triangles will be applied to quadrilaterals.