Lesson 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-3 SS |
| Book: | Lesson 2 |
| Printed by: | Guest user |
| Date: | Monday, 3 November 2025, 4:30 AM |
Description
Created by IMSreader
1. Lesson 2
Module 5: Geometry
Lesson 2: Quadrilaterals
Focus

iStockphoto/Thinkstock
Shown is a photograph of an inukshuk, which is a stone landmark created by the Inuit people of the Arctic region of North America. The inukshuk may have been used as a point of reference or a marker for travel routes.
Commonly, an inukshuk is a single stone positioned in an upright manner. In the photograph here, the inukshuk resembles a human being. An inukshuk that resembles a human being is called an inunnguaq. Many of the stones that make up this figure resemble simpler geometric shapes. Can you identify the quadrilaterals in the photograph? In this lesson you will find out what characteristics make up a quadrilateral.
Lesson Outcome
At the end of this lesson you will be able to solve problems that involve quadrilaterals.
Lesson Questions
You will investigate the following questions:
- How can the properties of quadrilaterals be used to help solve problems?
- How do the properties of quadrilaterals affect quadrilaterals’ shape and size?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 2 Assignment (Download the Lesson 2 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms
Materials and Equipment
- calculator
- ruler
- protractor
1.1. Launch
Module 5: Geometry
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson you should be able to understand the terms parallel, perpendicular, and diagonal.
1.2. Are You Ready?
Module 5: Geometry
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
Using the diagrams, answer the following questions.
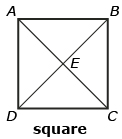
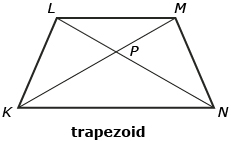
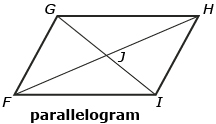
- Fill in the blanks with perpendicular, diagonal, or parallel.
- In the parallelogram, name a set of sides that are parallel. Answer
- In the square, diagonal BD is perpendicular to what? Answer
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 5: Geometry
Refresher
To review the term parallel, visit Parallel at the Mathematics Glossary.
To review the term perpendicular, visit Perpendicular at the Mathematics Glossary.
To review the term diagonal, visit Diagonal at the Mathematics Glossary.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 5: Geometry
Discover
Take a look around and you will see that there are many different types of quadrilaterals. Are you aware of the properties that make each type of quadrilateral unique? Complete Try This 1 to explore some of the properties of quadrilaterals and discover the names given to specific quadrilaterals.
Try This 1
Open Quadrilateral Demonstration Applet. Follow the instructions given in the questions. Analyze each constructed quadrilateral. Record your findings in a table like the one shown after each set of instructions.
- Click and drag the corners of the quadrilateral until all side lengths are equal and each enclosed angle is 90°. Look above the quadrilateral. What specific name is given to this shape? Record this name in the first column of the table, and complete the rest of the information about this quadrilateral.
- Move the top right and bottom right corners to the right so each angle is 90°. Record the name and information in the table.
- Move the top right corner left and then move the top left corner to the right, keeping the top and bottom lines parallel. Record the name and information in the table.
- Move the corners so the top and bottom are the same length and parallel. Adjust the left and right sides so they are the same length and parallel. Make sure the enclosed angles are not 90°. Record the name and information in the table.
- Move the corners so all sides are equal and the enclosed angles are not 90°. Record the name and information in the table.
- Move a corner away from the centre of the quadrilateral until two sides are equal and the other two sides are equal. Record the name and information in the table.
Type of Quadrilateral Pairs of Equal Sides (opposite or adjacent) Number of Equal Sides Pairs of Parallel Sides Number of Equal Angles (right angles or not right angles)
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or in a group, share your responses to Try This 1 and address the following questions:
- In any given quadrilateral, what is the sum of the interior angles?
- Trapezoids can be classified as right trapezoids or isosceles trapezoids. From your knowledge of triangles and the terms right and isosceles, determine when a trapezoid is right or isosceles.
![]() If required, place a summary of your discussion in your course folder.
If required, place a summary of your discussion in your course folder.
1.5. Explore
Module 5: Geometry
Explore
In Try This 1, you may have noticed that a quadrilateral is a polygon made up of four sides, four angles, and four vertices—hence the name quad, meaning “four,” and lateral, meaning “side.” The different types of quadrilaterals can be classified as a square, rectangle, trapezoid, parallelogram, rhombus, or kite. The four interior angles of any of these types of quadrilaterals will always add up to 360°.
Self-Check 1
Use your answers from Try This 1 to work through “Classifying Quadrilaterals Interactive.” As you complete this activity, make any changes necessary to your table from Try This 1.
In the next Try This, you will explore the properties of different quadrilaterals using the measurements of the sides, angles, and diagonals.
Try This 2
Use your textbook to explore the measurements of specific quadrilaterals. You will look at the quadrilaterals shown in “Discuss the Ideas” on pages 192 to 194 of the textbook. Use a ruler and protractor to complete this table. The first quadrilateral has been completed for you.
| Type of Quadrilateral | Measures of Corner Angles | Angles That Are Equal | Sides That Are the Same Length | Sides That Are Parallel | Are the lengths of diagonals the same? | Do the diagonals intersect at 90°? |
Square (question 1 on page 192) |
∠A = 90° ∠C = 90° ∠D = 90° |
∠A = ∠B = ∠C = ∠D | AB = BC = CD = AD | AB is parallel to CD; BC is parallel to AD |
yes | yes |
Rectangle (question 3 on page 192) |
∠A = |
|||||
Right Trapezoid (question 4 on page 193) |
∠A = |
|||||
Isosceles Trapezoid (question 4 on page 193) |
∠E = |
|||||
Parallelogram (question 1 on page 194) |
∠A = |
|||||
Rhombus (question 1 on page 194) |
∠W = |
|||||
Kite (question 1 on page 194) |
∠P = |
1.6. Explore 2
Module 5: Geometry
From Try This 1 and Try This 2, you should have noticed that quadrilaterals can be classified according to the properties of the quadrilateral.
| Square |  |
|
| Rectangle | 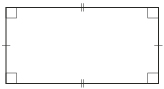 |
|
| Trapezoid | 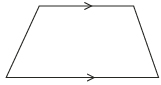 |
|
| Parallelogram | 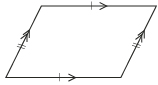 |
|
| Rhombus | 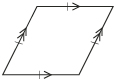 |
|
| Kite | 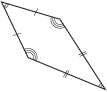 |
|
| Right Trapezoid | 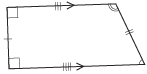 |
|
| Isosceles Trapezoid | 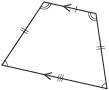 |
|
1.7. Explore 3
Module 5: Geometry
Self-Check 2
- Identify the quadrilateral in each photograph by its specific name.

Adapted from iStockphoto/Thinkstock

Adapted from Hemera/Thinkstock

Adapted from iStockphoto/Thinkstock

Adapted from Hemera/Thinkstock
Answer
![]()
- Answer “Build Your Skills” questions 1 and 2 from pages 198 and 199 of the textbook. Answer
1.8. Explore 4
Module 5: Geometry
You have explored the different properties of quadrilaterals and how to classify quadrilaterals based on the properties of the shape.
Quadrilaterals are extremely important in the construction of all building types. Without accurate measurements of lengths and angles, the structural integrity of a building can become extremely hazardous! Can you explain why?

first house: iStockphoto/Thinkstock; second house: iStockphoto/Thinkstock; third house: iStockphoto/Thinkstock
In the next Try This, you will explore how to solve problems that involve quadrilaterals.
Try This 3

Hemera/Thinkstock
Quaid has recently purchased a new one-ton pickup truck. He wants to install an extra fuel tank in the truck box so he won’t have to stop as frequently to refuel. He needs to get the tank custom-manufactured since he also wants the truck box to accommodate pulling a fifth-wheel trailer. The fuel tank needs to be in the shape of a prism with the specific dimensions shown.
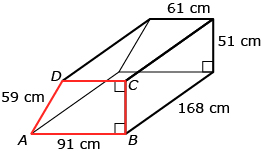
- What type of quadrilateral is figure ABCD (as shown in the diagram)? Explain your answer.
- Calculate the area of figure ABCD.

- Calculate the volume of the prism.

- How many litres of fuel can the tank hold?

1.9. Explore 5
Module 5: Geometry
In Try This 3, you may have found that the base of the prism was a right trapezoid. For an example of how to solve problems involving the volume of prisms, read “Example 1” on pages 193 and 194 of the textbook.
Self-Check 3
Add the following terms to your copy of Glossary Terms:
- square
- rectangle
- rhombus
- parallelogram
- trapezoid
- right trapezoid
- isosceles trapezoid
- kite
The word trapezoid is often used in the United States to describe a quadrilateral that has two sides parallel. The word trapezium is sometimes used in the United Kingdom to describe a quadrilateral that has two sides parallel. The word trapezium has its origins from the Greek word trapezion, which means “small table.”
1.10. Connect
Module 5: Geometry
Complete the Lesson 2 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
There is no Project Connection in this lesson.
1.11. Lesson 2 Summary
Module 5: Geometry
Lesson 2 Summary

© claudiu paizan/27277661/Fotolia
In this lesson, you looked at quadrilaterals and different ways to classify quadrilaterals based on their properties. You studied that a quadrilateral is a polygon with four sides and that the interior angles add up to 360°. You studied the specific properties of squares, rectangles, trapezoids, parallelograms, rhombuses, and kites. You also looked at situations in construction where quadrilaterals might be used.
In the next lesson, you will explore other types of polygons.




