Print bookPrint book

Lesson 3

Site: MoodleHUB.ca 🍁
Course: Math 30-3 SS
Book: Lesson 3
Printed by: Guest user
Date: Monday, 15 September 2025, 12:07 PM

Description

Created by IMSreader

Table of contents

1. Lesson 3

Mathematics 30-3 Module 5

Module 5: Geometry

 

Lesson 3: Regular Polygons

 
Focus

 

This is a photograph of a walkway made with stone pavers that are in the shape of regular polygons.

© kenny/436682/Fotolia

Stone pavers are one way to build a walkway or patio near a home. Have you ever laid a walkway or patio using stone pavers? The photograph is an example of a walkway built with stone pavers that are in the shape of regular polygons. What is the name of the polygon used? What do you notice about the sides and angles of each polygon? Can the type of polygon shown be divided into other shapes?

 

In this lesson, you will explore different regular polygons and determine some of the properties of regular polygons. You will then use these properties to help solve problems that involve regular polygons.

 

Lesson Outcomes

 

At the end of this lesson you will be able to

  • solve problems that involve regular polygons
Lesson Question


You will investigate the following question:

  • How can the properties of regular polygons be used to help solve problems?
Assessment

 

Your assessment may be based on a combination of the following tasks:

  • completion of the Lesson 3 Assignment (Download the Lesson 3 Assignment and save it in your course folder now.)
  • course folder submissions from Try This and Share activities
  • additions to Glossary Terms and Formula Sheet
  • work under Project Connection
Materials and Equipment
  • paper
  • cardboard or foam core board
  • ruler
  • scissors
  • glue stick
  • calculator


1.1. Launch

Mathematics 30-3 Module 5

Module 5: Geometry

 

Launch

 

Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.

 

Before beginning this lesson you should be able to recognize lines of symmetry.



1.2. Are You Ready?

Mathematics 30-3 Module 5

Module 5: Geometry

 

Are You Ready?

 

Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.

 

Determine the number of lines of symmetry for the objects shown.

 

  1. This is a pink heart.

    Answer

  2. This is a yellow star.

    Answer

 

If you answered the Are You Ready? questions without difficulty, move to Discover.

 

If you found the Are You Ready? questions difficult, complete Refresher.



1.3. Refresher

Mathematics 30-3 Module 5

Module 5: Geometry

 

Refresher

 

This is a play button that opens Line of Symmetry.
Work through Line of Symnetry.

Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.



1.4. Discover

Mathematics 30-3 Module 5

Module 5: Geometry

 

Discover
 

A polygon is a closed figure made up of three or more straight line segments. What do you think a regular polygon is? In Try This 1, you will explore the idea of regular polygons.

 

Try This 1

 

Use Regular Polygons to complete the questions shown here.

 

 

This is a play button that opens up Regular Polygons.

  1. Complete a table like the one shown.

    Number of Sides Name Are all sides of equal length? Are all interior angles equal? Are any lines parallel? How many lines of symmetry are there?
    5          
    6          
    7          
    8          
    9          
    10          
    11          
    12          
  2. All shapes used in the applet were regular polygons. In previous lessons you studied equilateral triangles and squares, which are both regular polygons. What do you think is the definition of a regular polygon?
  3. When do regular polygons have parallel sides? When do regular polygons not have parallel sides?
  4. What do you notice about the shape of a polygon as the number of sides increases?

course folder Save your responses in your course folder.



1.5. Explore

Mathematics 30-3 Module 5

Module 5: Geometry

 

Explore

 

In Try This 1, you may have noticed the following properties of regular polygons.

  • All sides are equal.
  • All interior angles are equal.
  • If there is an even number of sides, then the opposite sides are parallel.
  • If there is an odd number of sides, then there are no parallel sides.
  • The number of lines of symmetry is equal to the number of sides.
Self-Check 1
  1. Open “Exploring Shape Classification” and complete Level 2.

     
    This is a play button that opens up Exploring Shape Classification.

 

textbook

  1. Answer “Build Your Skills” question 1 on page 207 of the textbook. Answer

 

So far you have looked at some of the properties of regular polygons. In the next Try This, you will take a closer look at the measure of the interior angles of regular polygons and how these angles can be determined.

 

Try This 2

 

Open Regular Polygons and use the Size slider to change the size of each regular polygon.

 

 

This is a play button that opens up Regular Polygons.

  1. If the lengths of the sides of a regular polygon change, do the interior angles change? Explain.

Use the following information and the image to answer the remaining questions.

Each interior angle of a regular pentagon is 108°. You will discover how this measurement can be calculated using triangle properties.

 

 
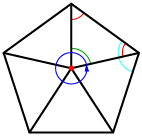
This is a regular pentagon with the centre indicated with a red dot.
  1. From the centre of the pentagon, draw line segments to each vertex, similar to the diagram shown. How many triangles are formed? Are the triangles identical? Why or why not?
  2. At the centre of the pentagon, the triangles meet. What is the angle indicated in dark blue at the centre of the pentagon?
  3. Using your answers from questions 2 and 3, what is the measure of the angle of each triangle where it touches the centre of the pentagon (indicated in green)?
  4. What type of triangles are formed inside the regular pentagon?
  5. Using your answers from questions 4 and 5, what are the measures of the angles inside the triangle, indicated in red at the outer edges of the triangle?
  6. What is the measure of each interior angle of the pentagon (indicated in light blue)?
  7. What is the sum of the interior angles of the pentagon?

course folder Save your responses in your course folder.

This angle is one full rotation of a circle.


1.6. Explore 2

Mathematics 30-3 Module 5

Module 5: Geometry

 

In Try This 2, you may have found that the triangles created inside a regular pentagon are identical and are isosceles triangles. Using your knowledge of isosceles triangles, you would have determined the measure of each interior angle of the regular pentagon. To see how the interior angle of a regular polygon can be determined, view Interior Angles of a Regular Polygon. Select the Play button for each step to continue.

 

 

This is a play button that opens Interior Angles of a Regular Polygon.

As you saw in Interior Angles of a Regular Polygon, the measure of each interior angle and the sum of the interior angles of a regular polygon can be determined using the formulas given here.

 

For an n-sided regular polygon, the following are true:

 

 


 
the sum of interior angles = 180°(n − 2)

 

In the next Try This, you will use these formulas to determine the measure of each interior angle and the sum of the interior angles for regular polygons.

 

Try This 3
  1. Complete a table like the one shown.

    Regular Polygon Name Number of Sides, n Measure of Each Interior Angle Sum of Interior Angles

    This is a blue triangle.

     

    		 equilateral triangle 3    

    This is a red square.

     

    		 square 4    

    This is a yellow pentagon.

     

    		 pentagon 5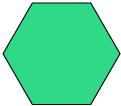    

    This is a green hexagon.

     

    		 hexagon 6    

    This is a brown octagon.

     

    		 octagon 8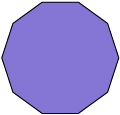    

    This is a purple decagon.

     

    		 decagon 10    
  2. What happens to the measure of each interior angle as the number of sides increases?
  3. Create a graph with the data from your table. Graph the number of sides, n, on the x-axis and the sum of interior angles, S, on the y-axis.
  4. What happens to the sum of the angles as the number of sides increases?

course folder Save your responses in your course folder.



1.7. Explore 3

Mathematics 30-3 Module 5

Module 5: Geometry

 

In Try This 3, you may have found that the measure of each interior angle increases as the number of sides of the polygon increases. The sum of the interior angles of a polygon increases by 180° each time a side is added to the polygon. As the number of sides of a polygon increases, the sum of the interior angles increases.

 

Self-Check 2


textbook

Answer “Build Your Skills” questions 3 and 4 from page 208 of the textbook. Answer

 

 

This is a photograph of chicken wire with a blue background.

iStockphoto/Thinkstock

 

Throughout the lesson, you have looked at properties of regular polygons. In the next Try This, you will try to construct a set of regular polygons and explore how this concept applies to the construction of materials.

 

A hexagon is a regular polygon that is often used in construction, as can be seen in the chicken wire shown. Hexagons can also be seen in honeycomb structures.

 

Try This 4


textbook

Read “Activity 5.3 Honeycomb Structures” on pages 205 and 206 of the textbook.

 

Complete “Part A: Assembly and Testing” questions 1 to 5 starting on page 205 of the textbook. Then answer questions 1 and 2 from “Part B: Assessing Honeycomb Structures” on page 206 of the textbook.

 

course folder Save your responses in your course folder.



1.8. Explore 4

Mathematics 30-3 Module 5

Module 5: Geometry

 

This is a photograph of a honeycomb that shows three regular hexagons fitting around one point.

Jupiterimages/Photos.com/Thinkstock

In Try This 4, you may have found that the shape of each cell of your structure is a hexagon. A hexagonal shape works well in a honeycomb structure, because each interior angle of a regular hexagon is 120°. Exactly 3 hexagons will fit together without a gap, because 120° divides evenly into 360° three times.

 

Squares are another regular polygon that would work in a honeycomb structure. Because 90° divides evenly into 360° four times, 4 squares would fit together without a gap. Honeycomb structures are useful because they provide strength but use less material, which makes them lighter. A honeycomb structure may be used in the core of a running shoe or a snowboard.

 

Self-Check 3


textbook

Answer “Practise Your New Skills” questions 6 and 7 from page 213 of the textbook. Answer

 



glossary

Add the following terms to your copy of Glossary Terms:

  • polygon
  • regular polygon

formula

Add the following formulas to your copy of Formula Sheet:

  • interior angle: for
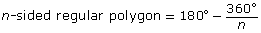
  • sum of interior angles: for n-sided regular polygon = 180°(n − 2)

1.9. Connect

Mathematics 30-3 Module 5

Module 5: Geometry

 

Connect

 

Lesson 3 Assignment


assessment

Complete the Lesson 3 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.

 

course folder Save your responses in your course folder.

 

Project Connection


assessment

You are now ready to apply your understanding of polygons to Module 5 Project: Designing a Yard. Go to the Module 5 Project, and complete Part 1: Inspiration for a Yard.

 

Going Beyond


textbook

Read “Roots of Math—Radial Symmetry in the Natural World” on page 201 of the textbook. Complete questions 1 and 2.

 

course folder Save your responses in your course folder.



1.10. Lesson 3 Summary

Mathematics 30-3 Module 5

Module 5: Geometry

 

Lesson 3 Summary

 

This is a photograph of a honeycomb that shows regular hexagons.

© margo555/35109581/Fotolia

In this lesson, you examined the properties of regular polygons. Regular polygons are useful in building and construction because of their unique properties. Different regular polygons fit together to form uniform or strong structures.

 

Regular polygons have the following properties:

  • All sides are equal.
  • All interior angles are equal.
  • If there is an even number of sides, then the opposite sides are parallel.
  • If there is an odd number of sides, then there are no parallel sides.
  • The number of lines of symmetry is equal to the number of sides.

You also explored how the interior angles of a regular polygon can be determined and found:

  • interior angle for
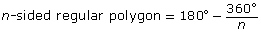
  • sum of interior angles for n-sided regular polygon = 180°(n − 2)

In the next lesson, you will look at how different shapes can be changed to create new shapes.