Lesson 6
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-3 SS |
| Book: | Lesson 6 |
| Printed by: | Guest user |
| Date: | Monday, 3 November 2025, 4:30 AM |
Description
Created by IMSreader
1. Lesson 6
Module 5: Geometry
Lesson 6: Sine Law
Focus

Hemera/Thinkstock
When you used the sine ratio in previous courses, you were working with right triangles. Not all problems involve right triangles. For instance, the original maps of Britain were based on survey work done between 1783 and 1853. In the early twentieth century, the British government realized that their maps were not completely accurate and decided to create new maps for all of Britain.
The triangulation method of surveying was used to complete the Retriangulation of Britain (1935–1962). Concrete pillars called trig points were created all around the country. These pillars became the vertices of triangles that were used to create accurate maps of Britain. Trigonometry played an important role in helping to calculate the angles and distances between trig points.
Trig-point locations were chosen for maximum visibility—the British didn’t have the luxury of creating right triangles. As a result, mathematics that is valid for all triangles, including oblique (non-right-angled) triangles, was used.
Today, if you were to use triangulation to measure distances around Lesser Slave Lake, you might end up with trig points and corresponding triangles at the locations shown.
There are no right-angled triangles in this diagram. You need to be certain that the method for solving this problem is valid for oblique (non-right-angled) triangles.
Lesson Outcomes
At the end of this lesson you will be able to
- use the sine law to determine an unknown length
- use the sine law to determine an unknown angle
Lesson Question
You will investigate the following question:
- How can the sine law be used to determine unknown sides and angles of oblique triangles?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 6 Assignment (Download the Lesson 6 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms and Formula Sheet
Materials and Equipment
- calculator
1.1. Launch
Module 5: Geometry
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson you should be able to
- determine the sine of a given angle
- determine an angle given the sine of that angle
- solve a proportion for an unknown
1.2. Are You Ready?
Module 5: Geometry
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Use your calculator to evaluate the following trigonometric ratios to four decimals places. (Make sure your calculator is set to degree mode.)
- sin 45°
- sin 19°
- sin 108°
- sin 153°
Answer - Use your calculator to find angle A in each of the following. (Round each answer to the nearest tenth.)
- sin A = 0.4572
- sin A = 0.9101
- sin A = 0.1887
- sin A = 0.7744
Answer - Solve the following equations for the unknown variable. (Round each answer to the nearest tenth.)
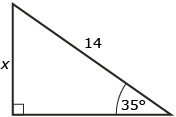
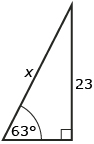
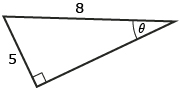
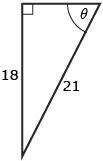
Answer - Solve for the unknown side x using the sine ratio:
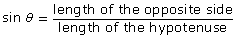
(Round each answer to the nearest tenth of a unit.) - Solve for the unknown angle theta (θ) using the sine ratio:
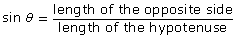
(Round each answer to the nearest degree.)
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 5: Geometry
Refresher
Work through Introduction to Trigonometry.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 5: Geometry
Discover
There are various relationships between side lengths and angles in a triangle. In Try This 1, you will explore one of these relationships.
Try This 1
When solving for angles, there are two calculator modes that can be used: radian and degree. Before beginning any trigonometry question within the Mathematics 30-3 course, ensure that your calculator is set in degree mode.
- Use a calculator to determine the sine of 114°. Round to two decimal places.
- Open Sine Law 1.

- Make sure that “Show A and a” is checked, and that “Show B and b” and “Show C and c” are not checked. In the diagram, “A” represents an angle and “a” represents the side length across from A. Copy the equation at the top of the screen and highlight where A, a, and their values are used in the equation.
- Try moving some of the vertices in the triangle around. Notice that A and a in the equation change as the values in the triangle change.
-
- Leave “Show A and a” visible and turn on “Show B and b” by checking the corresponding box. Watch for where the B and b values appear on the triangle. How are B and b related?
- Watch the two equations as you move one of the vertices of the triangle. What relationship do you notice between the equations?

- Using your response from part b., what can you conclude about
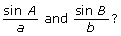
- Turn on “Show C and c” so all three boxes are checked. Move a point around again. How is
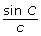 related to
related to 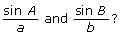
- Open Sine Law 2. This is very similar to Sine Law 1, but the equations are now written in the form
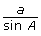 instead of in the form
instead of in the form 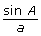 . How are
. How are 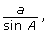
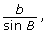 and
and 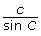 related?
related?

![]() Save your responses in your course folder.
Save your responses in your course folder.
1.5. Explore
Module 5: Geometry
Explore
In Try This 1, you explored a relationship that can be used with any triangle. This relationship is called the sine law and is often written as
![]()
![]() can also be written as
can also be written as ![]()
Again, this represents three separate equations:
In some situations, one version of the sine law is easier to use than the other.
Another way of writing this equation is to break it into three separate equations:
![]() means that the length of a side divided by the sine of the opposite angle is the same for all side-angle pairs in any triangle.
means that the length of a side divided by the sine of the opposite angle is the same for all side-angle pairs in any triangle.
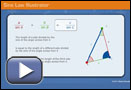
Watch Sine Law Illustrator to see this pictorially.
The sine law formulas reflect how mathematicians typically label triangles: sides are named with lowercase letters and angles are named with uppercase letters. Sides and their opposite angles are named with the same letter—for example, b and B.
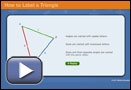
You may find it helpful to view How to Label a Triangle.
The sine law can be used to determine an unknown length in a triangle. Typically, the equations with the sines in the denominator are easiest to use when determining an unknown length. Try This 2 explores this idea.
Try This 2
- Draw the following triangle.
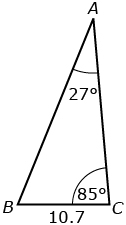
- Label the sides of the triangle with a, b, and c using the method described in How to Label a Triangle.
- Determine which of the following versions of the sine law would be best to find the length of the side between A and B. Explain your choice(s).

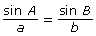
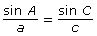
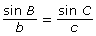
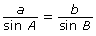
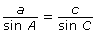
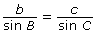
- Use your choice from part b. to determine the length of the side between A and B.

- Explain how you could determine the third angle of the triangle using the first two angles.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Writing a list of known values for the sides and angles of the triangle may be helpful. Place a “?” with the side you are trying to determine. One side and one angle will be left blank.
| Sides a = 10.7 b = c = ? |
Angles A = 27° B = C = 85° |
1.6. Explore 2
Module 5: Geometry
In Try This 2, you may have found that the sine law can be used to determine unknown lengths of a triangle. The two versions of the sine law you would use to solve for the lengh of the side between A and B are ![]() or
or ![]() . This is because the values A, a, and C are given and you want to determine c.
. This is because the values A, a, and C are given and you want to determine c.
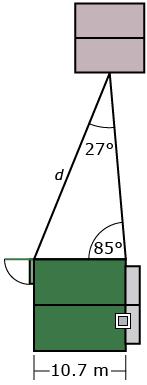
The following example shows how the triangle from Try This 1 can be used to solve a different problem.
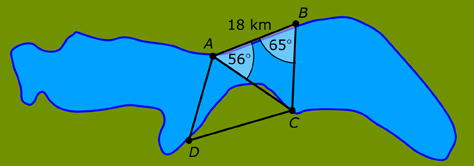
Khadija wants to build a walkway from her back door to a shed at the back of her yard. She needs to provide the length of the proposed walkway to a contractor in order to get a phone estimate for the cost. She knows her house is 10.7 m wide and has measured two angles, as shown in the diagram.
Khadija can use the sine law to determine the distance from her house to the shed (d on the diagram). Watch the solution in Determining a Distance Using the Sine Law. Pay attention to how substitution is used with the sine law.
To see another example of how a length can be determined using the sine law, read “Example 1” on page 251 of your textbook. Pay attention to how ∠C is determined.
Self-Check 1
Complete “Build Your Skills” questions 1, 3, 4, and 6 on pages 254 to 256 of your textbook. Answer
1.7. Explore 3
Module 5: Geometry

iStockphoto/Thinkstock
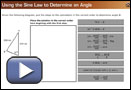
It is also possible to use the sine law to determine an unknown angle. The sine law equations with the sines in the numerator are typically easiest to use for determining unknown angles.
The following example shows how this can be done. Pay attention to when sin−1 is used while solving the problem.
Jeremy is learning how to use a compass in an orienteering course. The instructions he was given tell him that he must walk 70 m from checkpoint A to checkpoint B. He knows that checkpoint A is directly north of his location at checkpoint c, and checkpoint B is in a direction of N41°E. He also knows that checkpoint B is 105 m from checkpoint C. He begins by drawing a diagram to represent his situation.
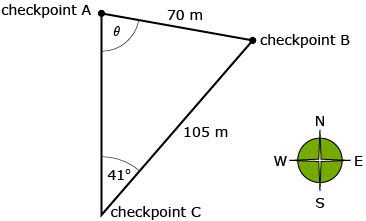
Jeremy needs to determine the direction to walk when going from checkpoint A to checkpoint B.
Orienteering is a sport where participants use a map and compass to find checkpoints or control points in an unfamiliar area. Orienteering is commonly done on foot, but other forms of transportation are possible.
When using a map and compass, one method of giving a direction is to use angles from north or south. For example: “N20°W” means start facing north and turn 20° towards the west. “S66°E” means start facing south and turn 66° towards the east.
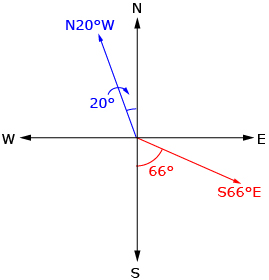
From the diagram he drew, he knows that once he determines ∠θ he will be able to state the direction as Sθ°E. Jeremy looks at the given information and recognizes that he can use the sine law to determine this angle. His solution can be seen in the animation Jeremy’s Solution.
When solving a sine law equation for an angle θ, you need to isolate sin θ and then use sin−1 on both sides of the equation.
Note that sin−1 is often the second function of the sin button on your calculator. Sometimes sin−1 is written as “arcsin” on calculators.
The equation sin θ = 0.5 can be solved for θ using the following steps:
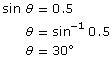
Check that you get sin−1 0.5 = 30 on your calculator.
In the next activity, you will correctly order the steps for determining an angle using the sine law.
1.8. Explore 4
Module 5: Geometry
To see another example of how the sine law can be used to determine an angle, read “Example 2” on page 252 of the textbook. Make sure you can follow what happens at each step.
Self-Check 2
- Answer “Build Your Skills” question 2 from page 254 of your textbook. Answer
- Complete “Property Perimeters 1 and 2” on page 253 of your textbook. Answer
Add sine law to your copy of Glossary Terms.
Add the following formulas to your copy of Formula Sheet:
1.9. Connect
Module 5: Geometry
Connect
Lesson 6 Assignment
Complete the Lesson 6 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
There is no Project Connection in this lesson.
1.10. Lesson 6 Summary
Module 5: Geometry
Lesson 6 Summary
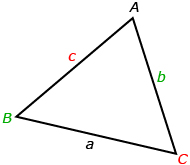
The sine law is a relationship that exists for all triangles, including right and oblique triangles. The sine law is usually written as ![]() or
or ![]() and can be used to determine unknown lengths and angles. When using the sine law, care needs to be taken when labelling the triangle. An angle and the side across from that angle will share the same letter.
and can be used to determine unknown lengths and angles. When using the sine law, care needs to be taken when labelling the triangle. An angle and the side across from that angle will share the same letter.
The sine law has many real-life contextual applications. In the following example, the length of a pipeline would have to be determined by using the given information and the sine law.
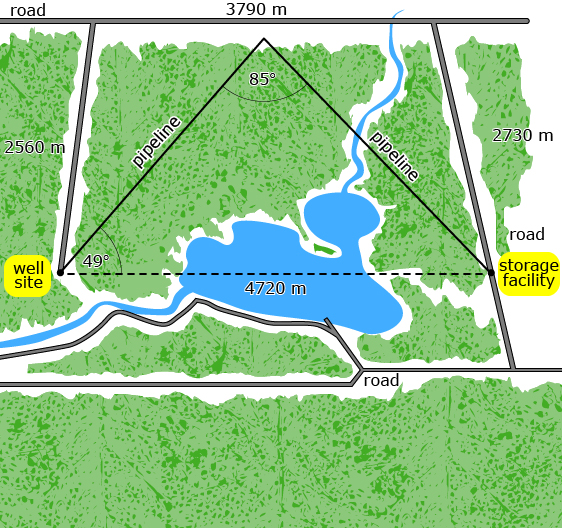
In the next lesson, you will explore the cosine law—another relationship between sides and angles in a triangle.