Lesson 7
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-3 SS |
| Book: | Lesson 7 |
| Printed by: | Guest user |
| Date: | Monday, 3 November 2025, 4:38 AM |
Description
Created by IMSreader
1. Lesson 7
Module 5: Geometry
Lesson 7: Cosine Law
Focus

Sean Murphy/Digital Vision/Thinkstock
There are many instances where direct measurement is not possible. If you can create a triangle using values that can be measured, you can often use trigonometry to calculate the value that is needed.
Jennifer and David are designing an obstacle course. They have a number of different tasks that participants need to complete, and they need to determine their materials list to set up all of the tasks. They are able to measure angles and distances for many of the tasks. However, some of the tasks are not easily measurable.
For the first task, people will need to hang on to a rope while crossing a rapidly flowing river that is about 1 m deep. Jennifer and David need to know the distance across the river to be sure that the rope is long enough. They don’t have a tape measure long enough to measure the river's width, so they decide to create a triangle using measurements that they can make in order to calculate this value.
David and Jennifer know the measures of the canyon walls and the angle at the bottom of the canyon, as shown in the following diagram. The rope corresponds to side c.
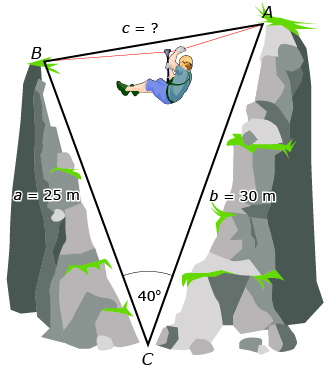
As you work through this lesson you will discover how David and Jennifer can determine the value of c and find the amount of rope they will need.
Lesson Outcomes
At the end of this lesson you will be able to
- determine an unknown length in a triangle using the cosine law
- determine an unknown angle in a triangle using the cosine law
Lesson Question
You will investigate the following question:
- How can the cosine law be used to solve problems?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 7 Assignment (Download the Lesson 7 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms
- work under Project Connection
Materials and Equipment
- calculator
1.1. Launch
Module 5: Geometry
Launch
Do you have the background knowledge and skills you need to complete this lesson successfully? Launch will help you find out.
Before beginning this lesson you should be able to
- determine the cosine of a given angle
- determine an angle given the cosine of that angle
- solve a proportion for an unknown
1.2. Are You Ready?
Module 5: Geometry
Are You Ready?
Complete these questions. If you experience difficulty and need help, visit Refresher or contact your teacher.
- Use your calculator (remembering to set your calculator to degree mode) to evaluate the following trigonometric ratios to four decimals places.
- cos 45°
- cos 28°
- cos 17°
- cos 53°
- Use your calculator to find ∠A in each of the following trigonometric ratios. (Round each answer to the nearest tenth.)
- cos A = 0.4572
- cos A = 0.9101
- cos A = 0.1887
- cos A = 0.7744
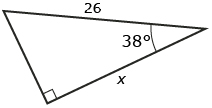
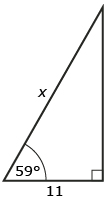
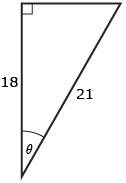
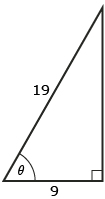
- Solve for the unknown side x using the cosine ratio:
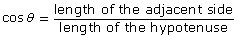
Round each answer to the nearest tenth of a unit. - Solve for the unknown ∠θ using the cosine ratio:
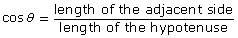
Round each answer to the nearest degree.
If you answered the Are You Ready? questions without difficulty, move to Discover.
If you found the Are You Ready? questions difficult, complete Refresher.
1.3. Refresher
Module 5: Geometry
Refresher
 Work through Introduction to Trigonometry.
Work through Introduction to Trigonometry.
Go back to the Are You Ready? section and try the questions again. If you are still having difficulty, contact your teacher.
1.4. Discover
Module 5: Geometry
Discover
In the next activity you will explore how Jennifer and David’s problem from Focus can be solved.
Try This 1
-
- Sketch a triangle to represent the problem from Focus.
- Explain why the Pythagorean theorem cannot be used to solve this problem.
- Write out all three equations of the sine law using values from the triangle you drew in part a.

- Explain why the diagram does not include enough information for you to use the sine law to determine length a.
Since the sine law cannot be used, you will have to explore a different relationship. One possibility is the cosine law. Open the Cosine Law Explorer.
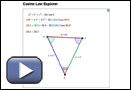
-
- The Cosine Law Explorer shows a cosine law equation and how it can be filled in using the values from the triangle. Explain where each value on the triangle is substituted into the original equation.
- Watch the last equation as you move a point around. What do you notice?
- Using your response from part b., what relationship can you predict between a2 and b2 + c2 − 2bc cos A? Do you expect this relationship will hold for all triangles?
- Use the equation a2 = b2 + c2 − 2bc cos A to solve Jennifer and David’s problem. The following steps may be useful.
- Determine which value on the triangle corresponds to each variable in the equation.
- Substitute the known values into the equation.
- Simplify the equation where possible
- Once you know what a2 is equal to, you can take the square root of both sides to determine the value of a.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
Share your responses with a classmate. In your sharing session, be sure to address the following points.
- How can you decide if there is enough information in a triangle to use the cosine law?
- How can you decide if there is enough information in a triangle to use the sine law?
1.5. Explore
Module 5: Geometry
Explore
In Discover, you were introduced to the cosine law in the form a2 = b2 + c2 − 2bc cos A. Like the sine law, the cosine law can be used with any triangle. The cosine law can be used if the length of the three sides are known (SSS) or the length of two sides and the enclosed angle are known (SAS).
The cosine law can be used on Jennifer and David’s scenario, since SAS applies. A possible solution to their problem follows.
| Write out the equation. | a2 = b2 + c2 − 2bc cos A |
| Substitute the known values. | a2 = 302 + 252 − 2(30)(25) cos 40° |
| Simplify each term. | a2 = 900 + 625 − 1149.1 |
| Simplify the expression. | a2 = 375.9 |
| Take the square root of both sides of the equation. | a = 19.4 |
Therefore, Jennifer and David will need a rope long enough to cross a 19.4-m gap.
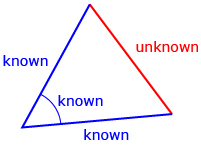
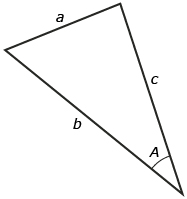
To label a triangle, use the same strategy used with the sine law, with angles given a capital letter and sides given a lowercase letter. Remember that an angle and the side across from the angle will get the same letter.
To use the equation a2 = b2 + c2 − 2bc cos A, always label the unknown side a and the angle across from the unknown side A. It does not matter which side you give the labels b and c to after a and A are labelled.
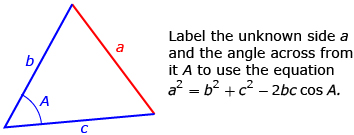
Watch Cosine Law Illustrator. This presentation reviews the relationship between the cosine law and the parts of a triangle.
Self-Check 1
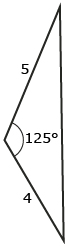
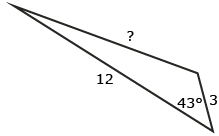
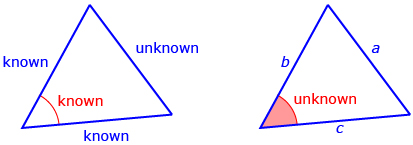
Label each triangle so you can use the cosine law, a2 = b2 + c2 − 2bc cos A, to determine the unknown side. (You don’t need to determine the unknown side.)
Once a triangle has been labelled properly, the cosine law (a2 = b2 + c2 − 2bc cos A) can be used to determine the length of the unknown side a. Read “Example 1” on page 261 of the textbook to see another example of how the cosine law can be used to determine the length of an unknown side. Pay attention to how the triangle was labelled before the cosine law was used.
Self-Check 2
1.6. Explore 2
Module 5: Geometry
Thus far you have used the cosine law to determine the length of an unknown side of a triangle. It is also possible to use the cosine law to determine the value of an unknown angle. Try This 2 explores this idea.
Try This 2

iStockphoto/Thinkstock
Sandra is taking the same orienteering course as Jeremy in Lesson 6. Sandra is standing at Checkpoint A and knows the distances between all the checkpoints, as shown in the diagram. In order to walk in the correct direction, she needs to determine the angle between Checkpoint B and Checkpoint C, represented by θ on the diagram.
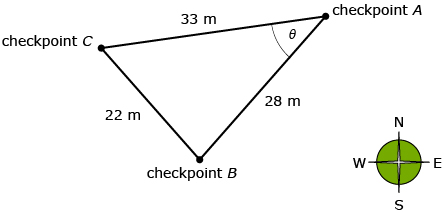
-
- Sketch the diagram. Label the sides and angles appropriately.
- Use a “guess and check” strategy with the equation a2 = b2 + c2 − 2bc cos A to determine the value of θ in the diagram.
-
- Using a “guess and check” strategy can take a long time. A better strategy may be to solve the formula for A. Try isolating A in the equation a2 = b2 + c2 − 2bc cos A using the following steps. Make sure to write each step on a new line.
- Subtract b2 and c2 from both sides of the equation.
- Divide both sides of the equation by −2bc.
- Apply the inverse cosine (cos−1) to both sides of the equation.

- Use the equation you determined in part a. to determine the value of θ in the diagram. How did this value compare to the one you determined in question 1. b?

- Using a “guess and check” strategy can take a long time. A better strategy may be to solve the formula for A. Try isolating A in the equation a2 = b2 + c2 − 2bc cos A using the following steps. Make sure to write each step on a new line.
![]() Save your responses in your course folder.
Save your responses in your course folder.
If you know all three sides of a triangle, you can use the cosine law to determine an unknown angle. It is possible to rearrange the equation a2 = b2 + c2 − 2bc cos A to allow you to determine unknown angles more easily.
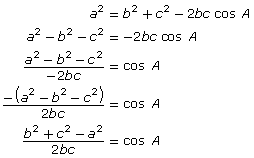
The equation ![]() can be used to determine cos A. To determine the degree measurement of A, find the inverse cosine (cos−1) of both sides of the equation.
can be used to determine cos A. To determine the degree measurement of A, find the inverse cosine (cos−1) of both sides of the equation.
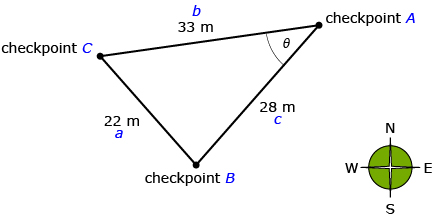
This equation can be used to determine the unknown angle in Try This 2 as follows.
| Write out the equation. | ||
| Substitute the known values. | ||
| cos A = 0.7516… |
|
When entering fractions on a calculator, extra care must be taken with brackets. The easiest approach is to always put the numerator in brackets and the denominator in brackets.
For this example, you would enter the following in your calculator: |
| A = cos−1 (0.7516…) | Use the inverse cosine (cos−1) to determine A. | |
| A = 41.268…° | The rounded value of A is 41.268…°. | |
| A = 41° | Round to the nearest degree, unless instructed otherwise. | |
Read “Example 2” on pages 262 and 263 of the textbook to see how all three angles of a triangle can be determined if you know all three sides.
Self-Check 3
Add the following formulas to your copy of Formula Sheet:
- a2 = b2 + c2 − 2bc cos A
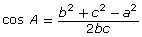
1.7. Connect
Module 5: Geometry
Connect
Lesson 7 Assignment
Complete the Lesson 7 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are now ready to complete the final part of Module 5 Project: Designing a Yard. Go to Module 5, and complete Part 3: Roof Trusses, as well as the conclusion component of the project.
As this is the final part of your project, be sure you review the rubric to ensure that you have completed all parts of the project to the best of your ability. When finished, submit your final project to your teacher.
1.8. Lesson 7 Summary
Module 5: Geometry
Lesson 7 Summary
In this lesson you explored the cosine law. The cosine law is useful when you are given three sides of a triangle or two sides and the angle between them. Just as in the sine law, the cosine law can be used with any triangle. To determine an unknown side, the equation a2 = b2 + c2 − 2bc cos A can be used. To determine an unknown angle, the equation ![]() can be used.
can be used.