Lesson 3
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 30-3 SS |
| Book: | Lesson 3 |
| Printed by: | Guest user |
| Date: | Tuesday, 4 November 2025, 2:39 AM |
Description
Created by IMSreader
1. Lesson 3
Module 6: Measurement
Lesson 3: Tolerances
Focus

iStockphoto/Thinkstock
Many industries use mass production methods that require parts and components that are made in different shops and possibly overseas. When a machinist is asked to build a part for an engine, the measurements of the part will need to be within a range of acceptable values so it will fit correctly. This idea connects directly to the idea of tolerances.
Lesson Outcomes
At the end of this lesson you will be able to
- demonstrate an understanding of tolerance
- apply tolerance to different situations involving measurement
Lesson Questions
You will investigate the following questions:
- How is tolerance applied in different situations?
- Why is there a need for tolerance in manufacturing?
- How is tolerance related to precision?
Assessment
Your assessment may be based on a combination of the following tasks:
- completion of the Lesson 3 Assignment (Download the Lesson 3 Assignment and save it in your course folder now.)
- course folder submissions from Try This and Share activities
- additions to Glossary Terms
- work under Project Connection
1.1. Discover
Module 6: Measurement

Creatas/Thinkstock
Discover
Try This 1
When moving furniture pieces into a home, you need to consider if the pieces will fit through the door. If a standard exterior door is 36 ± 2 in wide and 82 ± 2 in high, will each of the pieces of furniture in the following table fit through the door?
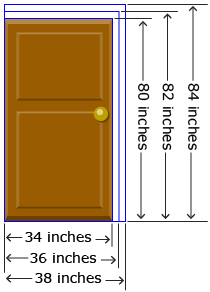
Furniture |
Length |
Width |
Height |
Illustration |
King-Size Mattress |
80 ± 0.5 |
76 ± 0.5 |
10 ± 0.5 |
iStockphoto/Thinkstock |
Couch |
90 ± 0.5 |
39 ± 0.5 |
31 ± 0.5 |
iStockphoto/Thinkstock |
Dining Room Table |
78 ± 0.5 |
40 ± 0.5 |
29 ± 1 |
Adapted from Comstock/Thinkstock |
Chest of Drawers |
41 ± 0.5 |
21 ± 0.5 |
49.5 ± 0.05 |
Hemera/Thinkstock |
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 1
With a partner or in a group, consider your answers to Try This 1, along with the following questions.
- What are the ranges of values for the dimensions of the door?
- Will some of the pieces fit one way but not another?
- Describe which way each piece will best fit through the door.
![]() If required, place a summary of your discussion in your course folder.
If required, place a summary of your discussion in your course folder.
1.2. Explore
Module 6: Measurement
Explore
tolerance: the range of acceptable dimensions
Source: MathWorks 12 Student Book/Teacher Guide.
(Vancouver: Pacific Educational Press, 2011.)
In the Discover activity, you may have noticed that some of the furniture pieces will fit through the door one way but not the other way. The doorway is only big enough for some of the pieces to be carried through. The range of measurements for the width and height of the door is called the tolerance.
Tolerance is highly important when it comes to industry and manufacturing.
To reduce the costs of manufacturing, blueprints are created to cover, in detail, all necessary materials and measurements. Since measurement tools have varying degrees of accuracy and precision, the measurements displayed on the blueprint must include some tolerance. The measurements are shown with a plus or minus (±) symbol to indicate the tolerance margin.
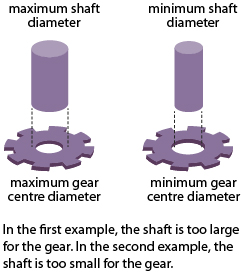
Extra consideration needs to be taken when determining measurement tolerances for manufacturing pieces that connect or slide against each other within the final product. For example, gears and shafts must align to fit one another.
The maximum diameter of the shaft must be able to fit into the minimum diameter of the gear’s centre, or vice versa, as shown in the illustration on the right.
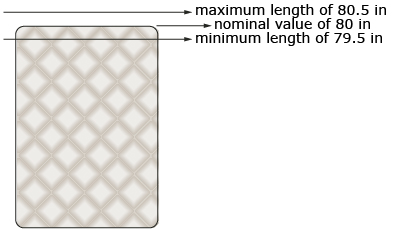
Blueprint measurements show a target for the measurement dimensions. The actual measurements must fall within the range of the target. For example, recall from Discover that the length of a king-size bed is 80 ± 0.5 in.
The nominal size is 80 in, and the tolerance is “plus or minus 0.5” in. This means that the actual manufactured bed should have a length that falls within 80 + 0.5 in and 80 − 0.5 in. The maximum value is 80.5 in, and the minimum value is 79.5 in.

Jupiterimages/ Photos.com/Thinkstock
There are always slight variations in the size of manufactured parts. Previously you were introduced to the term nominal value.
This term helps to describe manufacturing tolerance.
nominal value: the target value for the measured quantity
manufacturing tolerance: the difference between the maximum acceptable dimension and the minimum acceptable dimension
It can be expressed in several ways:

- nominal value
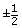 (tolerance)
(tolerance) - minimum value

- maximum value

Notice that the way a tolerance is written resembles the form in which measurement uncertainty is expressed. It is important to remember that a tolerance is not an uncertainty, but rather the acceptable range of a given measurement.
Source: MathWorks 12 Student Book/Teacher Guide.
(Vancouver: Pacific Educational Press, 2011.)
The following activity will allow you to explore the idea of tolerances and tolerance notation.
Try This 2
Open the interactive activity Tolerance Interval. This activity allows you to set a nominal value and tolerance for a centimetre ruler. The acceptable values then show up in red. When an object is clicked, a larger version will appear for you to measure. Use the interactive to answer the following questions.
- A hockey puck is supposed to have a diameter of 7.6 ± 0.2 cm. Is this size of hockey puck acceptable?
- A bakery wants its loaves of bread to be
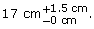 Is the size of this loaf of bread acceptable?
Is the size of this loaf of bread acceptable? - Wrenches 1 and 2 are acceptable sizes, while wrenches 3 and 4 are not acceptable. Determine a possible tolerance for the wrench size.
- Determine a tolerance in the form
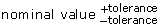 so the difference between the minimum and maximum is 0.8 cm and the banana is the minimum acceptable value.
so the difference between the minimum and maximum is 0.8 cm and the banana is the minimum acceptable value. - Determine a tolerance in the form
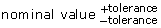 so the difference between the minimum and maximum is 0.8 cm and the banana is the maximum acceptable value.
so the difference between the minimum and maximum is 0.8 cm and the banana is the maximum acceptable value.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Share 2
With a partner or in a group, share your answers from Try This 2 and answer the following questions.
- Are there different ways that you could write solutions to questions 4 and 5 from Try This 2? Explain.
- Rewrite your solutions to questions 4 and 5 from Try This 2 using different nominal values.
![]() Record your shared responses in your course folder.
Record your shared responses in your course folder.
1.3. Explore 2
Module 6: Measurement
In Try This 2 you should have determined the tolerance by calculating the difference between the maximum and minimum acceptable dimensions of the object you were measuring. You also learned several different ways you can express this tolerance. You will now apply this knowledge by writing the specifications for a design.
Self-Check 1
Turn to page 93 of the textbook, and complete “Example 1.” Check your work with the solution that follows on pages 93 and 94.
In Self-Check 1 you practised finding the nominal value and the maximum and minimum values. The difference between the maximum and minimum values is the tolerance. In the next Try This you will apply this knowledge to plumbing in a home. Sometimes when you are not working from blueprints, you have to make some assumptions about what the maximum and minimum values would be.
Try This 3

Hania is renovating her basement and has just finished running drainpipes for the sink, toilet, and shower. She has a plumbing inspector check her work. After taking some measurements, he tells Hania that the slopes for some of her drains are not correct. He explains that horizontal drain lines need to be steep enough for material to move. However, if they are too steep, the liquids move faster than the solids and the drain may clog. The illustration shows a list of angles that he checked.
- Estimate the maximum allowable drain angle for a horizontal drain. What assumptions did you need to make in finding your estimate?
- Estimate the minimum allowable drain angle for a horizontal drain. What assumptions did you need to make in finding your estimate?
- Express this tolerance using the following four notations, which were discussed earlier:
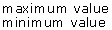
- nominal value
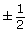 (tolerance)
(tolerance) 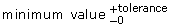
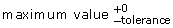
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.4. Explore 3
Module 6: Measurement
In Try This 3 you had to make assumptions about the maximum and minimum values for the angle of the drain. However, you could reasonably assume that as long as the angle of the drain was between the smallest acceptable value, 5.0°, and the largest acceptable value, 7.8°, it would pass inspection. You are now going to apply this in another common renovation application.
Self-Check 2
Go to page 95 of the textbook, and work through “Example 2.” Check your work with the solution that follows on pages 95 and 96.

iStockphoto/Thinkstock
When installing drainpipes or cutting holes for electrical outlets, the tolerance of the measurements is significant. The tolerance in measurements varies according to what is being measured and whether or not it has to fit with other pieces. In the next Try This you will have to decide which side of the tolerance range should be used when constructing a wooden stool.
You may have had an experience in either a construction technologies class or a fashion studies class that required careful measuring and cutting skills in order to piece parts of the final project together. The following Try This activity will expose you to the measurement decisions that need to be made while cutting and assembling a wooden stool.
Try This 4
![]()
Go to page 98 of the textbook, and complete “Activity 2.3: Tolerances in Carpentry.”
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.6. Connect
Module 6: Measurement
Complete the Lesson 3 Assignment that you saved in your course folder at the beginning of the lesson. Show work to support your answers.
![]() Save your responses in your course folder.
Save your responses in your course folder.
Project Connection
You are now ready to apply your understanding of tolerances to Module 6 Project: Project Measurement. Go to the Module 6 Project, and complete Part 3: Apply tolerances to your component. Once you are finished applying tolerances, complete the Project Checklist: Assemble the planning kit.
![]() Save your responses in your course folder.
Save your responses in your course folder.
1.7. Lesson 3 Summary
Module 6: Measurement
Lesson 3 Summary

Jupiterimages/ BananaStock/Thinkstock
In this lesson you discovered how tolerance relates to industry and manufacturing. It’s important for hand- or machine-crafted parts to be within certain tolerance levels so that they can be assembled and fit together properly.




