Print bookPrint book

Module 7 Summary

Site: MoodleHUB.ca 🍁
Course: Math 30-2 SS
Book: Module 7 Summary
Printed by: Guest user
Date: Monday, 15 September 2025, 1:36 AM

Description

Created by IMSreader

Table of contents

1. Module 7 Summary

Mathematics 30-2 Module 7

Module 7 Summary

 

In this module you investigated the following question: How can exponents and logarithms be used to solve problems that involve growth and decay?

 

Exponents and logarithms can be used to model growth, such as the rate a tree grows, and decay, such as the half-life of a radioactive element. Exponents and logarithms can both be useful when working with very large or very small values, such as pH or earthquake magnitude.

 

You learned about the characteristics of an exponential function and how exponential functions can be used to solve problems. You also learned about the characteristics of logarithmic functions, how logarithms can be used to solve problems, and how logarithmic scales can be used for data with an extreme range of values. You used the laws of logarithms to manipulate expressions with logarithms and to solve exponential equations. Finally, you determined regression equations for data that was logarithmic and exponential.

 

This shows the image of a cross-section of a human head. This is a photo of a universal indicator used to determine the pH of a solution.

left: Comstock/Thinkstock; right: © Schlierner /32104381/Fotolia


In the Module 7 Project: At the Movies, you described exponential and logarithmic graphs, solved various exponential and logarithmic problems in context, and applied your knowledge of regressions to information about your favourite movie.

 

The following chart lists some of the key ideas that you learned in each lesson.

 

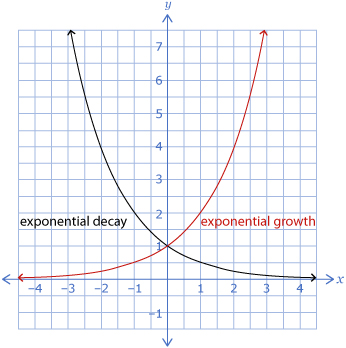
Lesson 1

Exponential functions can be used to model growth and decay.

 

This graph shows exponential growth and exponential decay.
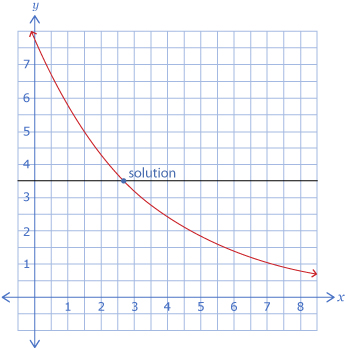
Lesson 2

Exponential equations can be solved using common bases or graphically.

 

This diagram shows a horizontal line intersecting an exponential decay function. The intersection is labelled “solution.”
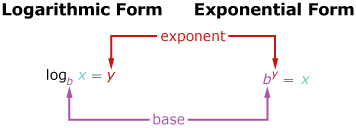
Lesson 3

The expression y = ax ↔ x = loga y can be used to convert between exponential and logarithmic forms of an equation.

 

This diagram shows an expression in logarithmic form and in exponential form. In logarithmic form, it is written as the base b logarithm of x equals y. In exponential form, c to the power of y equals x. The y variables are labelled “exponent” and the b variables are labelled “base.”

Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill Ryerson, 2011.
Reproduced with permission.
Lesson 4

Logarithmic functions can be increasing or decreasing.

 

This graph shows an increasing logarithmic function and a decreasing logarithmic function.
Lesson 5

The laws of logarithms (shown below) can be used to change logarithmic expressions.

 

 

logb M + logb N = logb(M × N)

 

 

 

 

logb (MN) = n logb M
Lesson 6

Exponential equations can be solved by taking the logarithm of both sides of the equation and then using the power law of logarithms to remove the exponent.
Lesson 7

Regression equations can be determined for exponential and logarithmic data. The natural logarithm, ln, is often used in logarithmic regression equations, as in ln x = loge x, where e ≈ 2.72.