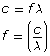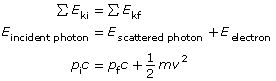Module 6
| Site: | MoodleHUB.ca 🍁 |
| Course: | Physics 30 SS |
| Book: | Module 6 |
| Printed by: | Guest user |
| Date: | Wednesday, 17 December 2025, 6:19 AM |
Description
Created by IMSreader
1. Module 6
Module 6—Wave-Particle Duality and Quantum Physics
Module Introduction
In Module 5 you looked at many experiments that proved that electromagnetic radiation (EMR) behaves like a wave. In the late 1800s and into the 1900s new experiments showed that the behavior of EMR was more complex than initially believed. Scientists built upon their previous knowledge to develop a new model for light and the behaviour of atoms as physics transitioned from classical physics to quantum physics.
In Module 6 you will learn about the idea of the quantum. You will see some of the work done by Planck, Einstein, Millikan, and de Broglie. You will also be introduced to the wave-particle duality of electromagnetic radiation.
In Module 6 evidence related to the quantum model and wave-particle duality will be explored in relation to
-
blackbody radiation and the photon as a quantum of EMR
-
the photoelectric effect and the conservation of energy
-
the Compton effect and the conservation of momentum and energy
1.1. Big Picture
Module 6—Wave-Particle Duality and Quantum Physics
 Big Picture
Big Picture

© Fedorenko Oleg Nikolaevich/shutterstock
At the turn of the 20th century, classical physics described electromagnetic radiation, such as visible light, using a wave model that was supported by the observations you explored in Module 5. It was also at this time that new evidence started to emerge which could not be explained using classical physics. Thus, a new “quantum” theory of electromagnetic radiation was born.

© Dana Bartekoske/shutterstock
This new evidence is related to how electromagnetic radiation is absorbed and emitted by various materials. For example, as molten metal is heated in a blast furnace it emits energy in a wide spectrum of radiation, including infrared heat apparent to those standing nearby, visible light (as seen in the photo on the right), and ultraviolet light. At increasing temperatures, more energy is emitted in specific wavelengths. This is similar to a stove burner that is black when cold and appears increasingly red as it becomes hot. There is a specific relationship between the temperature of an object and the spectrum of radiation it emits.
Other evidence is related to the absorption of electromagnetic radiation. If electromagnetic radiation of sufficient energy is incident on a photovoltaic cell (solar panel) an electrical current is produced which is proportional to the intensity of the incident radiation.
Such evidence is explained using the concept that energy transfers are quantized or bundled in packets called “photons.” Each photon has a specific amount of energy that is related to its wavelength or frequency. Furthermore, the conservation of momentum, a principle applied to physical objects, can also be demonstrated with X-rays revealing the dual particle and wave nature of electromagnetic radiation.

© Tobias Machhaus/shutterstock
Explaining the absorption and emission process required moving beyond classical physics and introducing the quantum model to explain and understand the wave-particle duality of electromagnetic radiation. In this module you will learn how the quantum model of light actually shows the wave-particle duality of EMR even though EMR was shown to behave like a wave in Module 5.
As you are working in Module 6, keep the following questions in mind:
- What is the quantum and how is it related to blackbody radiation?
- What is the photoelectric effect and how does it support wave-particle duality?
- How does the conservation of momentum and energy known as the Compton Effect support wave-particle duality?
 Module Assessment
Module Assessment
Each lesson has a teacher-marked assignment, based on work completed in the lesson. In addition, you will be graded on your contributions to the Discuss section of each lesson.
You will also be asked to complete Self-Check or Try This questions, which you should place in your Physics 30 course folder. These are not formally assessed but are a valuable way to practise the concepts and skills of the lesson. These activities can provide you with reflective feedback on your understanding of the lesson work.
You will be marked for your lesson work on the following items:
- Module 6: Lesson 1 Assignment
- Module 6: Lesson 2 Assignment
- Module 6: Lesson 3 Assignment
At the end of the module you will complete a module assessment that consists of two Diploma Exam-style written-response questions. The first question will assess your knowledge of the photoelectric effect and the second question will assess your knowledge of the Compton effect. You will find these questions in the Module 6 Summary and Assessment. If you have any questions contact your teacher.
1.2. In this Module
Module 6—Wave-Particle Duality and Quantum Physics
In This Module
In Module 6 evidence related to the quantum model and wave-particle duality will be explored in relation to
- blackbody radiation and the photon as a quantum of EMR
- the photoelectric effect and the conservation of energy
- the Compton effect and the conservation of momentum and energy
Lesson 1—Blackbody Radiation and the Quantum
In this lesson you will explore the relationship between colour and temperature and what is meant by a blackbody and blackbody radiation curves. You will also learn that blackbody radiation curves can be explained by assuming that energy is emitted from hot objects in discrete bundles, or photons, each capable of transferring a minimum quanta of energy.
-
How is blackbody radiation illustrated graphically?
-
What is the relationship between colour and temperature?
-
What is a quantum? What is a photon?
Lesson 2—The Photoelectric Effect
In this lesson you will investigate what is meant by the photoelectric effect and how it is described by quantum theory. You will also learn how the photoelectric effect supports the notion of wave-particle duality.
-
What is the photoelectric effect?
-
How is the photoelectric effect described by quantum theory?
-
How does the photoelectric effect support the notion of wave-particle duality?
Lesson 3—Compton, de Broglie, and Wave-Particle Duality
In this lesson you will learn about the Compton effect, how it is related to the conservation of energy and momentum, and that it supports wave-particle duality. Under the context of the de Broglie hypothesis, you will also explore whether a particle can behave as a wave if light can behave as a particle.
-
What is the Compton effect and how is it related to the conservation of energy and momentum?
-
How does the Compton effect support wave-particle duality?
-
If light can behave as a particle, can a particle behave as a wave?
-
What is de Broglie’s wave equation?
1.3. Lesson 1
Module 6—Wave-Particle Duality and Quantum Physics
Lesson 1—Blackbody Radiation and the Quantum
 Get Focused
Get Focused

© Alexey Stiop/shutterstock
How can you tell when a stove element is hot? When it is off, it appears black and is cool to the touch. Turn the electric current on and it starts to warm up, slowly taking on a red glow that becomes more and more intense. We have come to associate the colour red with things that are hot, like the coals in a fire or the small wires in your toaster. At even greater temperatures, objects appear white, indicating the presence of many wavelengths of light being emitted. The filament in an incandescent light bulb is a good example of something that is nearly white-hot.
These simple observations indicate that there is a relationship between the temperature of a body and the wavelength of the electromagnetic energy it emits. This relationship is described by blackbody radiation curves. Initially, the relationship between temperature and the wavelength of the emitted radiation didn’t seem very complex, but classical physics was not able to explain it. Hence, quantum physics was born to explain the relationship between temperature and the wavelength of emitted radiation.
In this lesson you will learn about blackbody radiation and the idea of the quantum.
In this lesson you will answer the following essential questions:
- How is blackbody radiation illustrated graphically?
- What is the relationship between colour and temperature?
- What are a quantum and a photon?
 Module 6: Lesson 1 Assignment
Module 6: Lesson 1 Assignment
Your teacher-marked Module 6: Lesson 1 Assignment requires you to submit responses to the following:
- Assignment—A 1, A 2, A 3, A 4, A 5, A 6, and A 7
- Discuss—D 3
The other questions in this lesson are not marked by the teacher; however, you should still answer these questions. The Self-Check and Try This questions are placed in this lesson to help you review important information and build key concepts that may be applied in future lessons.
After a discussion with your teacher, you must decide what to do with the questions that are not part of your assignment. For example, you may decide to submit to your teacher the responses to Try This questions that are not marked. You should record the answers to all the questions in this lesson and place those answers in your course folder.
1.4. Page 2
Module 6—Wave-Particle Duality and Quantum Physics
 Explore
Explore
Blackbody Radiation
In 1862 German physicist Gustav Kirchhoff introduced the term blackbody to describe a hypothetical object that absorbs all of the electromagnetic radiation (EMR) that falls on it. In theory, the energy of all the absorbed EMR causes the blackbody to heat up and become a perfect radiator, emitting energy back to the environment in the form of EMR. Some of the EMR can be seen in red- or white-hot objects and longer wavelengths can be felt as heat. The heating element on a stove can be considered a blackbody radiator—you can feel the infrared EMR and see the visible EMR at sufficient temperatures.
The relationship between temperature and colour can be summarized using a Blackbody Spectrum simulation. Open the simulation and see what happens when you adjust the temperature using the slider.
blackbody radiation curve: a graph of the intensity of EMR versus wavelength for an object at a given temperature
incandescent: glowing with heat
As illustrated below, the simulation shows the observed colour of an object at the temperature indicated on the slider. In this example, a blackbody radiation curve shows the distribution of energy by wavelengths released by an incandescent light bulb when it is 3045 Kelvin (2772°C). Notice that the bulb emits most of its energy in wavelengths slightly larger than those of visible light, which is infrared heat. Interestingly, this is why an incandescent light bulb is very inefficient at producing light—90% of the energy it consumes produces infrared heat rather than visible light!
One interesting thing about blackbody radiation curves is that you can use an object’s curve, along with its observed colour, to tell the object’s temperature!
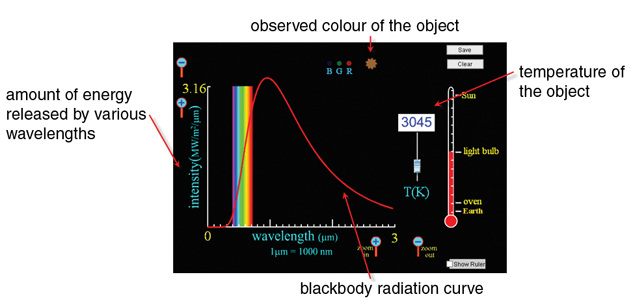
© The University of Colorado, under the GNU General Public License (GPL)
 Try This
Try This
TR 1. Using the Blackbody Spectrum simulation, complete the third relationship between colour and temperature.
- Extremely hot, glowing objects, such as stars, emit a continuous range of wavelengths, making them appear white.
- At a given temperature, the energy emitted by a hot object comprises a specific range of wavelengths, giving it a unique colour.
- At _______ temperatures, an object emits more blue light; at _______ temperatures, it emits more red light.
 Self-Check
Self-Check
SC 1. Using the radiation curves in the simulation, explain why a light bulb appears white while an oven element only has a slight red glow. What does this imply about the temperature of the filament in a light bulb compared to that of an element in a stove?
 Self-Check Answer
Self-Check Answer
Contact your teacher if your answers vary significantly from the answers provided here.
SC 1.
Light Bulb
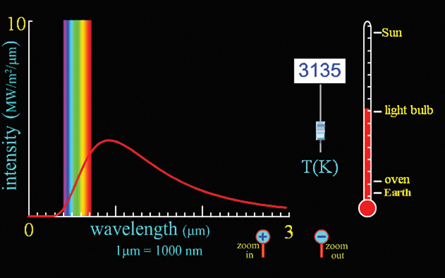
The bulb appears white because it emits some energy in wavelengths that span across the visible range of wavelengths. The longer, infrared wavelengths are not seen but are felt as heat.
Stove Element
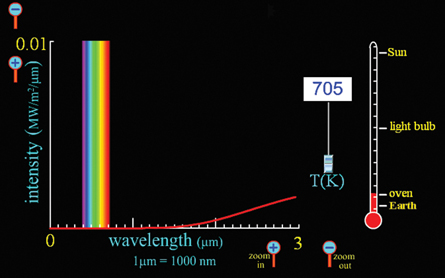
Zooming in several times along the intensity axis reveals that oven temperatures release energy with wavelengths that approach the red end of the visible spectrum. The element in an oven will start to appear red when it reaches temperatures near 1300 K. (Note the inside of an oven is much cooler than this, which is why the element cycles on and off and the entire oven does not glow red hot.) You can adjust the temperature on the simulation upward to find the exact temperature at which red light will start to appear.
The temperature of the filament in a light bulb is much higher than that of a stove element, even during the heating cycle.
 Read
Read
Read pages 704 and 705 of the textbook for more information on blackbody radiation and curves. Note that some of the radiation curves shown in the text are related to frequency rather than to wavelength, as seen in the simulation.
The Quantum
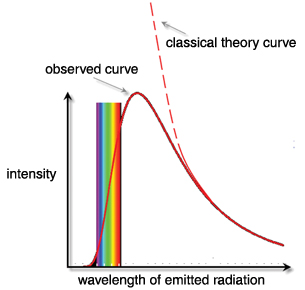
The explanation for blackbody radiation and, in particular, the shape of the radiation curves, could not be found in classical physics. For example, classical physics predicts that as an object heats up it should start releasing energy in shorter and shorter wavelengths, since this is the most efficient way to release energy. At very high temperatures, the amount of energy released is maximized by the release of ever-shorter wavelengths.
quantum (pl. quanta): the smallest bundle or packet of energy that a given wavelength or frequency of EMR can possess
Planck’s formula: EMR energy is the product of the number of quanta, Planck’s constant, and the frequency of the radiation,
However, the blackbody radiation curves produced by hot objects show that even at extremely high temperatures, most of the energy is released by relatively long wavelengths with little or no energy released by very short wavelengths. The explanation for the shape of the observed curves came from Max Planck in the year 1900. He could account for the shape by assuming that there was a specific amount of energy that any given wavelength of radiation could exchange with its environment. The term quantum refers to this specific energy, and it is related to the wavelength of the radiation by Planck’s formula.
Planck’s EMR energy is the product of the number of quanta, Planck’s constant, and the frequency of the radiation |
|||||||||||||||
|
|||||||||||||||
* n refers to the whole number of quanta that make up the total amount of energy (E) transferred by the radiation; therefore, n = 1, 2, 3, 4, . . . . |
|||||||||||||||
Note that Planck’s formula applies equally to wavelength as it is related to frequency by the universal wave equation.
|
Planck’s formula represents a fundamental shift in theory. In this system the amount of energy that can be exchanged between radiation and its surroundings is quantized, or limited to whole-number multiples of the smallest unit of energy—the quantum. Furthermore, the value of each quantum is equal to the product of Planck’s constant and the frequency of the radiation (E = hf). The concept of the quantum effectively ended classical physics and gave birth to quantum physics.
photon: one quantum of light
 Read
Read
Read “Einstein, Quanta, and the Photon” on page 706 of the textbook.
 Try This
Try This
TR 2. Complete “Practice Problems” 1, 2, and 3 on page 706 of the textbook.
TR 3. Complete “Practice Problems” 1, 2, and 3 on page 707 of the textbook.
TR 4. Complete “Practice Problems” 1 and 2 on page 708 of the textbook.
Energy and the Spectrum
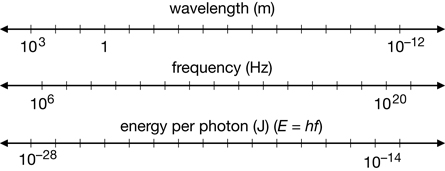
Planck’s formula associates photon energy with the frequency of radiation, expanding the electromagnetic spectrum to show the energy of various classifications of EMR.
 Module 6: Lesson 1 Assignment
Module 6: Lesson 1 Assignment
Remember to submit your answers to A 1, A 2, A 3, A 4, A 5, A 6, A 7, and D 3 to your teacher as part of your Module 6: Lesson 1 Assignment.
A 1. Why couldn’t classical physics explain blackbody radiation curves?
A 2. What is the frequency of a 13.0-eV photon?
A 3. What is the wavelength of a 4.30×10–19-J photon?
A 4. How many photons with a wavelength of 532 nm are released each second by a 5.0-mW laser?
A 5. As a safety precaution when working with lasers, scientists wear red-coloured glasses that will block all colours but red. Why is a red laser safer than a blue laser?
A 6. A person lives near a 50-kW radio tower. Why is it safe to live near the high-power radio tower but dangerous to be exposed to an X-ray machine that uses 7.5 kW?
A 7. Why did the introduction of the photon effectively end classical physics? What does this mean for the Christiaan Huygens theory that light is a series of waves and Thomas Young’s double-slit experiment?
 Discuss
Discuss
D 1. Develop a mnemonic that will help you remember the order of radiation given in “Figure 14.6” on page 709 of the textbook. RMIVUXG = Radio Microwave Infrared Visible Ultraviolet X-ray Gamma. Post your mnemonic in the discussion area for your class.

© cloki/shutterstock
D 2. Using the concepts of quanta and photons, explain the difference between a 100-W and 40-W light bulb if they both produce only green light. Post your answers in the discussion area for the following questions:
- Why does the 100-W bulb appear brighter than the 40-W bulb?
- Why would you expect the 100-W bulb to feel hotter than the 40-W bulb?
- If 10% of the energy consumed by the bulb produces green light of 500 nm, how many green photons does each bulb produce each second? How does this support your explanation of brightness?
D 3. Read the answers from two other students for D 2 and improve your own answer. Explain what you learned from reading the other students’ answers and if or how you changed your own solution.
Discussion Scoring Guide
Principles involved: energy of a photon and power |
||||
Criteria |
Level 1 (Below Standard) |
Level 2 (Approaching Standard) |
Level 3 (Standard) |
Level 4 (Above Standard) |
Knowledge |
||||
Demonstrates understanding of the situation, physics principles and technology, and their connections. |
Demonstrates a vague and sometimes incorrect understanding of the physics principles involved. Obvious irrelevant or missing information. |
Demonstrates a basic understanding of the physics principles involved. May exhibit minor mistakes or vague information or application to the situation. |
Demonstrates a good understanding of the physics principles involved and applies them properly to the given situation. All necessary information is given. |
Demonstrates a superior understanding of the physics principles involved and their application to the situation. All applications are considered in detail. |
Reflection |
||||
The post shows reflection on one’s own and other students’ work. Contributes to the group discussion. |
Does not make an effort to participate. Seems indifferent to discussion. | Occasionally makes meaningful reflections on the group’s efforts or discussions. Marginal effort is shown to become involved with the group or discussion. | Frequently makes meaningful reflections on the group’s efforts and presents relevant viewpoints for consideration by the group. Interacts freely with group members. | Regularly attempts to motivate the group discussion and delve deeper into concepts. Interacts freely and encourages all group members. |
Content and presentation of discussion summary |
||||
The information is logically arranged in a clear and concise manner. |
The information is poorly organized with many concepts implied. Irrelevant or rambling sentences make reading difficult. | The information is somewhat organized with implied concepts. Excessive words or awkward sentences are used, which hinder reading. | The information is well-organized and logically arranged. All concepts are explicitly explained. There are a few awkward but understandable sentences. | The information is well-organized and very easy to understand. Well-worded sentences make reading pleasurable. |
1.5. Page 3
Module 6—Wave-Particle Duality and Quantum Physics
 Reflect and Connect
Reflect and Connect

© john austin/shutterstock
Blackbody radiation curves can be explained using quantum theory. Consider the stove element. When you turn on the stove, the element absorbs electrical energy and begins to heat up. When the temperature of the stove element exceeds that of the surroundings, it releases energy with photons in the infrared range of wavelength and frequency. Each photon transfers a specific amount of energy. As the element’s temperature continues to rise, more energy is radiated. This can be achieved by emitting more photons in the infrared wavelength, each removing a quantum of energy or by emitting photons with a greater frequency (visible light) such that each photon transfers a larger quantum of energy. According to the radiation curves, both strategies apply. At greater temperatures the curve moves upward on the intensity scale, meaning more photons are released. At high temperatures, the curve also moves laterally to higher frequency (smaller wavelength) radiation, adding more photons that transfer higher individual quanta of energy. This explains why the stove element begins to glow red as it continues to heat up. At peak temperature it will release most of the energy in infrared photons and the remaining energy in visible light photons.
In the photo on the right, the yellow-to-red colouring in the coil indicates that the temperature is greater near the centre and coolest on the outside. This simple observation and the quantum theory that explains it represent a shift from classical physics to quantum physics.
 Module 6: Lesson 1 Assignment
Module 6: Lesson 1 Assignment
Remember to submit the Module 6: Lesson 1 Assignment to your teacher.
1.6. Page 4
Module 6—Wave-Particle Duality and Quantum Physics
 Lesson Summary
Lesson Summary
In this lesson you focused on the following questions:
-
How is blackbody radiation illustrated graphically?
-
What is the relationship between colour and temperature?
-
What are a quantum and a photon?
In this lesson you learned that a blackbody refers to a hypothetical object that absorbs all of the electromagnetic radiation that falls on it. The absorbed energy causes the blackbody to heat up and become a perfect radiator, emitting energy back to the environment in the form of electromagnetic radiation. The intensity and wavelength (or frequency) of the emitted radiation can be used to construct a blackbody radiation curve. Such curves illustrate the emitted energy distribution in terms of wavelength (or frequency) versus intensity for a blackbody at various temperatures. The curves showed that as the temperature increased, the frequency and intensity of the emitted EMR also increased. Attempts to explain this using classical physics gave nonsensical solutions.
You also learned that the radiation curve can be explained by assuming that energy is emitted from hot objects in discrete bundles, or photons, each capable of transferring a minimum quanta of energy associated with its wavelength and frequency according to Planck’s formula, E = hf. Applying the formula to the electromagnetic spectrum reveals the energy of the photons in all the general classifications of the spectrum.
You also learned that for physics in general, the idea of the quantum marked the end of classical physics and the beginning of quantum physics by showing that light could be considered a photon, a particle.
Lesson Glossary
blackbody: any object that absorbs all EMR that falls on it and is capable of being a perfect emitter, releasing energy in the form of EMR
blackbody radiation curve: a graph of the intensity of EMR versus wavelength for an object at a given temperature
incandescent: glowing with heat
quantum (pl. quanta): the smallest bundle or packet of energy that a given wavelength or frequency of EMR can possess
photon: one quantum of light
Planck’s formula: EMR energy is the product of the number of quanta, Planck’s constant, and the frequency of the radiation
1.7. Lesson 2
Module 6—Wave-Particle Duality and Quantum Physics
Lesson 2—The Photoelectric Effect

© Adrian Matthiassen/shutterstock
 Get Focused
Get Focused
Solar panels are designed to convert the energy of electromagnetic radiation into useable electrical current. From powering hand-held calculators to charging batteries and providing household electricity, the solar cell is a carbon dioxide-free, renewable energy resource. It is also an excellent example of how photons interact with metal surfaces in a process that sheds light on the quantum nature of electromagnetic radiation.
Solar cells are just one variation of many applications that harness the photoelectric effect, a phenomenon in which electrons are emitted from a metal surface after absorbing energy from electromagnetic radiation. In this lesson you will explore the photoelectric effect and its relationship to quantum theory.
The evolution of both photoelectric technology and quantum theory occurred simultaneously. The first crude solar cells were developed at the turn of the 19th century after the interaction between radiation and metal surfaces was observed by Heinrich Hertz in his classic experiment to produce and detect EMR. In 1905 Einstein explained this effect using quantum theory and was awarded the Nobel Prize for it in 1921. By that time, quantum theory had become mainstream in scientific circles. In 1954 Bell Laboratories accidentally discovered that silicon, when mixed with certain metal impurities, was very sensitive to light. Four years later, in 1958, both Russian and American satellites deployed solar cell technology to power their satellites. Today, thanks to applications in space exploration and research and an understanding of quantum theory, photoelectric technology is deployed in countless applications, from automatic door openers, to remote pumping stations in northern Alberta, and even to the battery chargers that power the Spirit and Opportunity rovers on Mars.
In this lesson you will answer the following essential questions:
- What is the photoelectric effect?
- How is the photoelectric effect described by quantum theory?
- How does the photoelectric effect support the notion of wave-particle duality?
 Module 6: Lesson 2 Assignment
Module 6: Lesson 2 Assignment
Your teacher-marked Module 6: Lesson 2 Assignment requires you to submit responses to the following:
- Assignment—A 1, A 2, A 3, A 4, A 5, A 6, A 7, A 8, A 9, and A 10
- Discuss—D 2
The other questions in this lesson are not marked by the teacher; however, you should still answer these questions. The Self-Check and Try This questions are placed in this lesson to help you review important information and build key concepts that may be applied in future lessons.
After a discussion with your teacher, you must decide what to do with the questions that are not part of your assignment. For example, you may decide to submit to your teacher the responses to Try This questions that are not marked. You should record the answers to all the questions in this lesson and place those answers in your course folder.
1.8. Page 2
Module 6—Wave-Particle Duality and Quantum Physics
 Explore
Explore
 Read—The Photoelectric Effect
Read—The Photoelectric Effect
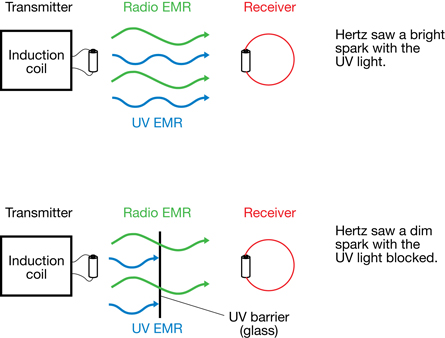
In 1887 during his investigations into Maxwell's Theory of Electromagnetic Waves (Module 5: Lesson 1), Heinrich Hertz discovered the photoelectric effect. As shown in the diagram above, Hertz found that the ultraviolet light produced by the spark in his radio transmitter greatly enhanced the spark that was observed at the receiver. This provided indirect evidence that the electrons in some metals are ejected when light of sufficient frequency contacts it. In Hertz’s experiment, the ultraviolet light produced by the spark at the transmitter supported the production of a spark at the receiver by ejecting electrons from its metal surface. When the ultraviolet light was blocked from reaching the receiver, the intensity of the sparks at the receiver was noticeably reduced.
The photoelectric effect is based on the fact that certain metallic surfaces lose their negative charges when exposed to ultraviolet light. Consider the apparatus illustrated below. When ultraviolet light is incident on a polished zinc surface, the negatively charged leaves of the electroscope fall. This indicates that the electroscope loses negative charge when ultraviolet light makes contact with the polished metal surface.
photoelectric effect: the emission of electrons when a metal is illuminated by EMR with a frequency greater than or equal to the metal’s threshold frequency
photoelectron: an electron emitted from a metal because of the photoelectric effect
threshold frequency: the minimum frequency that a photon can have to cause photoemission from a metal
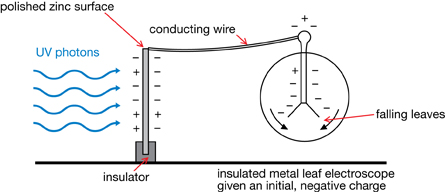
If the zinc plate is replaced with a non-metal surface such as glass, the electroscope is unaffected indicating that the photoelectric effect does not occur on the surface of insulators.
It was found that a few elements, namely the alkali metals (lithium, sodium, potassium, rubidium, and cesium), will eject electrons, commonly referred to as photoelectrons, when visible or UV light is incident on them. For this reason the alkali metals are commonly used in photoelectric cells and other devices that make use of the photoelectric effect. Metals from outside the alkali group will also eject photoelectrons but generally require higher frequency, higher energy EMR beyond the visible spectrum (UV, X-ray, and Gamma rays).
The following general observations have been made with regard to the photoelectric effect:
- Electrons are emitted instantly when EMR is incident on the surface. There is no time required for the electrons in the metal to build up energy before escaping.
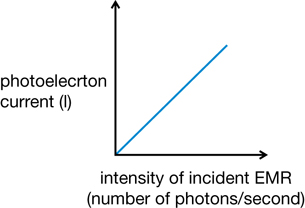
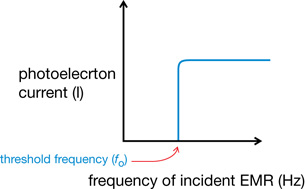
- A threshold frequency of EMR is required to cause the emission of photoelectrons. If the light shining on the photoelectric surface is below a certain frequency, there is no photoelectron emission regardless of the intensity, or brightness, of the light. If the frequency is higher than the threshold frequency, photoelectron emission occurs regardless of the intensity. This is the minimum frequency of EMR that causes the photoelectric effect for a specific metal.
- According to quantum theory, the intensity, or brightness, of the incident light indicates the number of photons being emitted. Therefore, bombarding a metal with many photons at a frequency lower than the threshold has no effect.
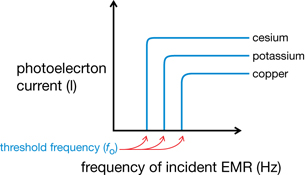
- Each type of metal has its own characteristic threshold frequency.
- When the frequency of the incident EMR increases beyond the threshold frequency, the kinetic energy of the released photoelectrons shows a corresponding increase. (A photoelectron is a regular electron ejected from a metal during the photoelectric effect.)
- If the light is at or above the threshold frequency, increasing the intensity will increase the number of photoelectrons, but not the energy of any individual photoelectron. The current (C/s) would increase because more electrons are released each second. This shows that the number of photoelectrons is proportional to the number of photons.
These general observations can be illustrated graphically.
Graph 1: Current vs. Intensity of Incident EMR
Graph 2: Current vs. Frequency of Incident EMR
Graph 3: Current vs. Frequency of Incident EMR for Various Metals
Read “The Photoelectric Effect” on pages 711 and 712 of your physics textbook for more information.
1.9. Page 3
Module 6—Wave-Particle Duality and Quantum Physics
The Photoelectric Effect and Quantum Theory
work function: the minimum energy that a photon can have to cause photoemission from a metal
Each metal has a specific work function.
Einstein explained the general observations for the photoelectric effect in 1905 using Planck’s quantum hypothesis. He proposed that the energy delivered by a single incident photon is defined by Ephoton = hf and that a certain amount of energy, called the work function, is required to free an electron from a metal surface. For example, it takes 4.70 eV of energy to eject an electron from copper, but only 2.30 eV of energy is required to free an electron from potassium. The work function (W) is related to the threshold frequency by Planck’s equation, W = hfo. Notice that in Graph 3 on the previous page the threshold frequency for both copper and potassium supports this idea. Copper has a higher threshold frequency than potassium since it requires more energy to free an electron. This means that when a photon with energy greater than that of a metal’s work function is incident on the surface, a photoelectron will be emitted.
Einstein’s theory also predicted that if an incident photon has more energy than the metal’s work function, the ejected photoelectron would leave with some kinetic energy, thus supporting the law of conservation of energy.
 Watch and Listen
Watch and Listen
© The University of Colorado, under the GNU General Public License (GPL)
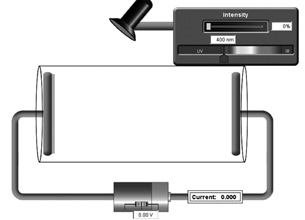
Experiments performed by Robert Millikan in 1916 provided the evidence to support Einstein’s photoelectric theory. A simulation will be used to explore a simplified version of this work.
SIM 1. Open the photoelectric effect simulation1 and adjust the intensity slider ( )
to 100% and select the (
)
to 100% and select the (![]() )
graph mode. With the graph showing, slide the intensity slider to 0% and back again to 100%. Does the observed graph match Graph 1 on the previous page? Explain this relationship and what “intensity” means in a quantum context.
)
graph mode. With the graph showing, slide the intensity slider to 0% and back again to 100%. Does the observed graph match Graph 1 on the previous page? Explain this relationship and what “intensity” means in a quantum context.
1© The University of Colorado, under the GNU General Public License (GPL)
In this simplification of Millikan’s experiment, photons above the threshold frequency strike a metal plate in an evacuated tube. A positive electrode connected to a power supply collects the emitted photoelectrons, thus establishing a photoelectric current.
When the power supply polarity is reversed, it produces an electric force that effectively repels the photoelectrons and slows the current. At sufficient voltage—called the stopping voltage or stopping potential difference—the photoelectric current observed in the ammeter drops to zero.
stopping voltage: the potential difference for which the kinetic energy of a photoelectron equals the work needed to move through a potential difference, V
SIM 2. With the intensity at 100% and the wavelength in the UV range, many photoelectrons contribute to the current in the circuit displayed in the yellow box. Click and drag the voltage slider on the battery ( ) to adjust the electric field in the tube. Observe the charge on each electrode. What happens to the motion of the photoelectrons? Explain why this happens.
) to adjust the electric field in the tube. Observe the charge on each electrode. What happens to the motion of the photoelectrons? Explain why this happens.
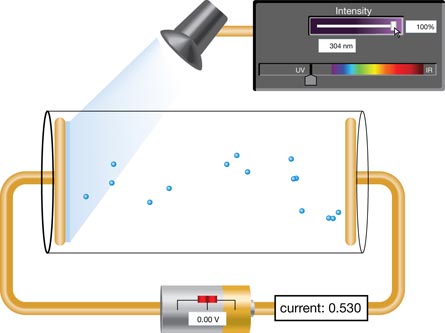
SIM 3. Set the photon wavelength to 298 nm and the intensity to 100%. Using the battery slider, determine the minimum voltage that brings the current to zero amps.
Vstop = __________________
Now change the intensity to 50%. Using the battery slider, determine the minimum voltage that brings the current to zero amps. How does changing the intensity affect the stopping voltage?
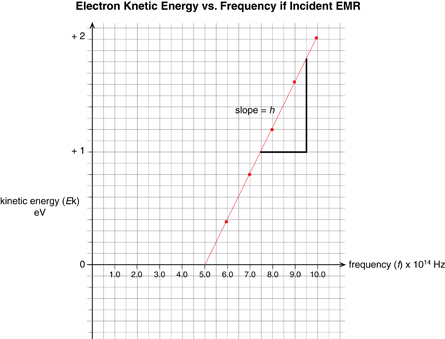
The voltage needed to "stop" the photoelectric current provides an indication of the kinetic energy of the photoelectrons. Recall that the energy of a charged particle in a uniform electric field is defined by E = Vq. In this instance, the equation can be written as Ek = qVstop, where q is the charge of an electron and Vstop is the minimum voltage required to halt the current. Therefore, measuring the voltage required to stop a photoelectric current gives the kinetic energy of the photoelectrons. Graphing the kinetic energy of the photoelectrons (as determined by the stopping voltage) versus the frequency of the incident radiation produces a graphical representation of the photoelectric effect.
SIM 4. Select the electron energy versus light frequency graph (![]() ) and vary the wavelength (and by extension the frequency) of the incident EMR (
) and vary the wavelength (and by extension the frequency) of the incident EMR (![]() ).
).
Sketch the graph of electron energy versus light frequency (as shown below).
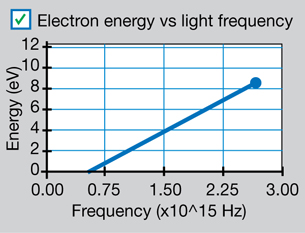
Your graph should be similar to the following graph, which was presented in Millikan’s 1916 investigation into the photoelectric effect.
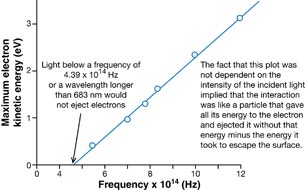
Physics (Pearson Education Canada, 2007) p714, fig 14.12. Reproduced with permission.
This graph is described mathematically by y = mx + b, where y is the kinetic energy of the photoelectrons, x is the frequency of the incident EMR, m is the slope of the line, and b is the y-intercept. Comparing this equation with the conservation of energy gives a mathematical expression for the photoelectric effect. According to the conservation of energy principle, the kinetic energy of the ejected photoelectron is equal to the difference between the energy of the incident photon and the work required to free it from the metal surface (the work function).
This can be stated mathematically (and compared to the graph equation) as follows:
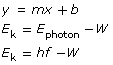
According to this equation, the slope of the line for photoelectron energy versus incident light frequency is equal to Planck’s constant. Therefore, the photoelectric effect provides an experimental way to measure Planck’s constant.
According to the conservation of energy principle, the kinetic energy of the ejected photoelectron is equal to the difference between the energy of the incident photon and the work required to free it from the metal surface (the work function). |
||||||||||||
|
||||||||||||
The energy of a charged particle in a uniform electric field is defined by
where q is the charge of an electron (1e– or 1.6 × 10–19 C) and Vstop is the minimum voltage required to stop the photoelectric current.
The energy of a photon, according to Planck’s formula is
where c is the speed of light, f is the frequency of the incident radiation and h is Planck’s constant in either joules or electron volts.
h = 6.63 × 10–34 J•s OR 4.14 × 10–15 eV•s
The work function can be defined by the minimum frequency that can cause photoemission, which according to Planck’s formula is |
Example Problem 1. What is the energy (in J and eV) of a photon of blue light that has a frequency of 6.67 × 1014 Hz?
Given
f = 6.67 × 1014 Hz?
Required
the energy of the photon
Analysis and solution
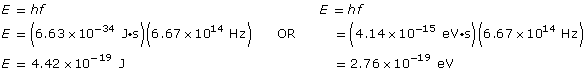
Paraphrase
The energy is 4.42 × 10–19 J or 2.76 eV.
Example Problem 2. Light with a wavelength of 600 nm is directed at a metallic surface that has a work function of 1.60 eV. What is the maximum kinetic energy (in J) of the emitted photoelectrons, their maximum speed, and the voltage needed to stop the photoelectric current?
Given
![]()
Required
the kinetic energy of the emitted photoelectrons, their maximum speed, and the voltage needed to stop the photoelectric current
Analysis and Solution
First convert the work function to joules.
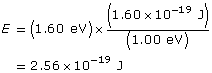
Find the maximum kinetic energy.
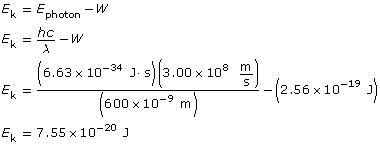
To determine the speed of the photoelectrons, you must use the kinetic energy expressed in joules; eV won’t work due to unit incompatibility!
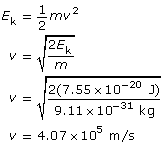
To find the stopping voltage,
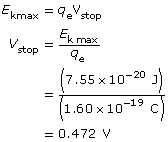
Paraphrase
The kinetic energy of the photoelectrons is 7.55 × 10–20 J; their maximum speed is 4.07 × 105 m/s; and the stopping voltage is 0.472 V.
Example Problem 3. An electron is ejected from a metal with a speed of 4.7 × 106 m/s. The threshold frequency of the metal is 7.8 × 1014 Hz. What is the wavelength of the incident photon?
Given
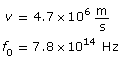
Required
the wavelength of the incident photon
Analysis and Solution

Paraphrase
The wavelength of the photon is 1.9 × 10–8 m or 19 nm.
 Self-Check
Self-Check
SC 1. You may check your understanding of the photoelectric effect using this photoelectric effect tutorial.
SC 2. You may check your understanding of the work function using this work function tutorial.
 Read
Read
Read “Millikan’s Measurement of Planck’s Constant” on pages 713 to 716 of your physics textbook for more information.
 Module 6: Lesson 2 Assignment
Module 6: Lesson 2 Assignment
Remember to submit your answers to A 1, A 2, A 3, A 4, and A 5 to your teacher as part of your Module 6: Lesson 1 Assignment.
While conducting research into the design of a light sensor, scientists measure the kinetic energy of photoelectrons that have been ejected from an unknown metal surface. The metal is exposed to various frequencies of EMR, and the stopping voltage is measured to obtain the kinetic energy of the photoelectrons. The following data is obtained:
Incident EMR frequency × 1014 Hz |
Kinetic energy of photoelectrons (eV) |
6.0 |
0.38 |
7.0 |
0.80 |
8.0 |
1.20 |
9.0 |
1.63 |
10.0 |
2.04 |
A 1. Using this data, plot a kinetic energy versus frequency graph, and use it to answer questions A 2 to A 5. You will find a blank graph in your Module 6: Lesson 1 Assignment.
A 2. According to your graph, what is the threshold frequency of the unknown metal? Label it on your graph.
A 3. Determine the work function of the unknown metal.
A 4. Using “Table 14.1” on page 712 of your textbook, identify the unknown metal.
A 5. Using your graph, determine the experimental value for Planck’s constant (in eV∙s). Label this value on your graph.
 Try This
Try This
TR 1. Complete “Practice Problems” 1 and 2 on pages 718 and 719 of your physics textbook.
TR 2. If you want more practise, you have the option of trying the Photoelectric Effect Practice Problems.
 Module 6: Lesson 2 Assignment
Module 6: Lesson 2 Assignment
Remember to submit your answers to A 6, A 7, A 8, A 9, and A 10 to your teacher as part of your Module 6: Lesson 1 Assignment.
A 6. What is the energy of a photon that has a wavelength of 460 nm?
A 7. A photoelectric surface has a work function of 2.00 eV. What is the threshold frequency of this surface?
A 8. A photon of frequency 8.2 × 1015 Hz is incident upon a photoelectric apparatus containing a metal whose threshold frequency is 3.6 x 1015 Hz. What is the stopping voltage?
A 9. Electrons are ejected from a photoelectric cell with a maximum kinetic energy of 1.20 eV. If the incident light has a wavelength of 410 nm, what is the work function of the cell?
A 10. Light with a wavelength of 425 nm falls on a photoelectric surface that has a work function of 2.0 eV. What is the maximum speed of any emitted photoelectrons?
 Discuss
Discuss
D 1. You are asked to explain the photoelectric effect in terms of energy to a student who missed the class. In your explanation, start with the energy of the incident EMR photons and finish with the energy of the stopping voltage. Make sure to include the following terms in your answer: threshold frequency, light intensity, photoelectron current, work function, photoelectron kinetic energy, and stopping voltage. Post your answer to the discussion area.
 Module 6: Lesson 2 Assignment
Module 6: Lesson 2 Assignment
Remember to submit your answer to D 2 to your teacher as part of your Module 6: Lesson 1 Assignment.
D 2. Read the answers to D 1 from at least two other students. Revise your answer from D 1 and include any changes you made and how they improved your answer.
Discussion Scoring Guide
Principles involved: Conservation of energy, light energy, electrical energy and voltage |
||||
Criteria |
Level 1 (Below Standard) |
Level 2 (Approaching Standard) |
Level 3 (Standard) |
Level 4 (Above Standard) |
Knowledge |
||||
Demonstrates understanding of the situation, physics principles and technology, and their connections. |
Demonstrates a vague and sometimes incorrect understanding of the physics principles involved. Obvious irrelevant or missing information. |
Demonstrates a basic understanding of the physics principles involved. May exhibit minor mistakes or vague information or application to the situation. |
Demonstrates a good understanding of the physics principles involved and applies them properly to the given situation. All necessary information is given. |
Demonstrates a superior understanding of the physics principles involved and their application to the situation. All applications are considered in detail. |
Reflection |
||||
The post shows reflection on one’s own and other students’ work. Contributes to the group discussion. |
Does not make an effort to participate. Seems indifferent to discussion. | Occasionally makes meaningful reflections on the group’s efforts or discussions. Marginal effort is shown to become involved with the group or discussion. | Frequently makes meaningful reflections on the group’s efforts and presents relevant viewpoints for consideration by the group. Interacts freely with group members. | Regularly attempts to motivate the group discussion and delve deeper into concepts. Interacts freely and encourages all group members. |
Content and presentation of discussion summary |
||||
The information is logically arranged in a clear and concise manner. |
The information is poorly organized with many concepts implied. Irrelevant or rambling sentences make reading difficult. | The information is somewhat organized with implied concepts. Excessive words or awkward sentences are used, which hinder reading. | The information is well-organized and logically arranged. All concepts are explicitly explained. There are a few awkward but understandable sentences. | The information is well-organized and very easy to understand. Well-worded sentences make reading pleasurable. |
1.10. Page 4
Module 6—Wave-Particle Duality and Quantum Physics
 Reflect and Connect
Reflect and Connect

© Krkr/shutterstock
Is light a wave? Is it a particle? Is it both?
The photoelectric effect supports the notion of wave-particle duality for electromagnetic radiation. The classical wave theory based on Maxwell’s electromagnetic waves was unable to explain several characteristics of the photoelectric effect. The instant release of photoelectrons when the EMR is incident on the metal meant that classical waves were not being continually absorbed until enough energy had accumulated to eject a photoelectron. The energy must be absorbed in bundles, or photons (light quanta), suggesting a particle nature for the incident EMR. There was also no clear relationship between the brightness, or intensity, of the EMR and the kinetic energy of the released photoelectrons. Again, this is understood by limiting the energy of each photon to a specific value, or light quanta.
The idea of light quanta (photons) treated EMR as a particle, which helped scientists understand the photoelectric effect. In combination with the wave-like characteristics of EMR from other experiments, the notion of wave and particle characteristics took on more meaning and, in doing so, promoted the notion of wave-particle duality.
 Module 6: Lesson 2 Assignment
Module 6: Lesson 2 Assignment
Remember to submit the Module 6: Lesson 2 Assignment to your teacher.
1.11. Page 5
Module 6—Wave-Particle Duality and Quantum Physics
 Lesson Summary
Lesson Summary
You explored the following questions in this lesson:
-
What is the photoelectric effect?
-
How is the photoelectric effect described by quantum theory?
-
How does the photoelectric effect support the notion of wave-particle duality?
In this lesson you learned that the photoelectric effect is characterized by the following general observations:
-
Electrons are emitted instantly when EMR is incident on the surface.
-
A threshold frequency of EMR is required to cause the emission of photoelectrons. If the light shining on the photoelectric surface is below a certain frequency, there is no photoelectron emission, regardless of the intensity, or brightness, of the light. If the frequency is higher than the threshold frequency, photoelectron emission occurs regardless of the intensity.
-
Each type of metal has its own characteristic threshold frequency and when the frequency of the incident EMR increases beyond the threshold frequency, the kinetic energy of the released photoelectrons shows a corresponding increase.
-
If the light is at or above the threshold frequency, increasing the intensity will increase the number of photoelectrons, but not the energy of any individual photoelectron.
![]()
These relationships were verified by Millikan’s experiments using stopping voltage to measure accurately the kinetic energy of the photoelectrons.
The photoelectric effect can also be illustrated graphically by plotting the photoelectron kinetic energy versus the frequency of the incident light. When this is done, the graph forms a straight line defined by y = mx + b, which means, according to the mathematical definition of the photoelectric effect, the slope of the line is equal to Planck’s constant and the x-intercept is equal to the threshold frequency of the metal.
Einstein’s explanation of the photoelectric effect treated EMR as if it had particle characteristics in terms of light quanta. Doing so helped scientists understand the photoelectric effect. In summary, the photoelectric effect, in combination with the wave-like characteristics of EMR from other experiments, supported the notion that EMR has both particle- and wave-like characteristics, thereby promoting the notion of wave-particle duality.
Lesson Glossary
photoelectric effect: the emission of electrons when a metal is illuminated by EMR with a frequency greater than or equal to the metal’s threshold frequency
photoelectron: an electron emitted from a metal because of the photoelectric effect
stopping voltage: the potential difference for which the kinetic energy of a photoelectron equals the work needed to move through a potential difference
threshold frequency: the minimum frequency that a photon can have to cause photoemission from a metal
wave-particle duality: the notion that EMR has both wave-like and particle-like characteristics
work function: the minimum energy that a photon can have to cause photoemission from a metal
Each metal has a specific work function.
1.12. Lesson 3
Module 6—Wave-Particle Duality and Quantum Physics
Lesson 3—Compton, de Broglie, and Wave-Particle Duality
 Get Focused
Get Focused
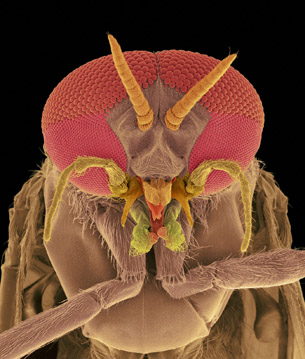
Copyright © 2007 Dennis Kunkel Microscopy, Inc.
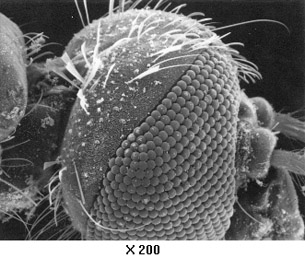
The image on the right is of a black fly’s head as seen through an electron microscope. At this resolution and magnification, it may not look like any fly you’ve ever seen! With the aid of an electron microscope, however, you can clearly see the details in the compound eyes and the skin-piercing mouthparts that it bites with. In fact, the resolution in this image shows details that cannot even be seen in a visible-light microscope. This is because visible light cannot be reflected from objects that are smaller than its wavelength. In effect, you can’t see an object that is smaller than about 400 nm using visible light. To see details that are even smaller, an electron microscope is needed.
The term “electron microscope” should seem odd to you now, since you’ve learned that an electron has been treated as a particle and that a microscope, which operates on the principles of reflection and refraction, should only apply to waves. How, then, could such technology work? Is it based on wave-particle duality? Who predicted that an electron could be used for microscopy, and why? In this lesson you will explore wave-particle duality.
In this lesson you will answer the following essential questions:
- What is the Compton effect and how is it related to the conservation of energy and momentum?
- How does the Compton effect support wave-particle duality?
- If light can behave as a particle, can a particle behave as a wave?
- What is de Broglie’s wave equation?
 Module 6: Lesson 3 Assignment
Module 6: Lesson 3 Assignment
Your teacher-marked Module 6: Lesson 3 Assignment requires you to submit responses to the following:
- Assignment—A 1, A 2, A 3, A 4, A 5, A 6, A 7, and A 8
- Discuss—D 2
The other questions in this lesson are not marked by the teacher; however, you should still answer these questions. The Self-Check and Try This questions are placed in this lesson to help you review important information and build key concepts that may be applied in future lessons.
After a discussion with your teacher, you must decide what to do with the questions that are not part of your assignment. For example, you may decide to submit to your teacher the responses to Try This questions that are not marked. You should record the answers to all the questions in this lesson and place those answers in your course folder.
1.13. Page 2
Module 6—Wave-Particle Duality and Quantum Physics
 Explore
Explore
The Compton Effect
Compton effect: an increase in wavelength of an X-ray as a result of its interaction with matter
Compton scattering: the scattering of an X-ray when it interacts with an electron
Einstein’s photon model of the photoelectric effect suggested that a photon behaves as a particle. Other experimental observations also supported the idea that a photon behaves as a particle. While experimenting with X-rays directed at graphite blocks, Arthur Compton observed what is now known as the Compton effect. He noticed that when X-rays are scattered by a graphite block, there is a subtle change in their wavelength and that this change is related to the angle at which the X-rays are scattered. The scattering of an X-ray when it collides with an electron is now known as Compton scattering.
Compton observed the energy and momentum of the incident X-ray, the scattered X-ray, and the electron and discovered that the collision demonstrated the conservation of momentum and energy—just as it would for an elastic collision between two particles. The experimental design is similar to that of a photoelectric effect, except using X-rays rather than lower energy EMR.
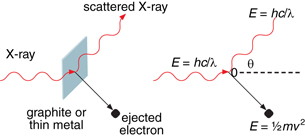
In terms of energy, Compton found that the total energy of the incident X-ray and the electron before the collision were equal to the total energy of the scattered X-ray and the ejected electron after the collision. This shows that the collision that occurred is perfectly elastic.
In terms of momentum, it is possible to generate an expression for the momentum of a wave using Einstein’s equation ![]() . Accordingly, mass and energy are just different forms of the same thing.
. Accordingly, mass and energy are just different forms of the same thing.
Manipulating the equation in terms of mass gives ![]() .
.
The familiar momentum equation ![]() can also be expressed in terms of mass:
can also be expressed in terms of mass: ![]() .
.
Putting the two equations together gives ![]() , since v = c for a photon travelling at the speed of light.
, since v = c for a photon travelling at the speed of light.
Substituting ![]() produces the following two equations that describe the momentum of a photon:
produces the following two equations that describe the momentum of a photon: ![]() .
.
By measuring the wavelengths of the incident and scattered X-rays as well as the velocity of the ejected electron, Compton was able to analyze the momentum involved in the collision between a photon and an electron. He determined that the total momentum of the incident X-ray photon was equal to the total momentum of the scattered X-ray photon and the ejected electron. Indeed, the collision appears to behave as a perfectly elastic collision between two particles.
 Self-Check
Self-Check
SC 1. Complete the “Concept Check” on page 721 of your physics textbook.
SC 2. Draw a vector addition diagram to show the conservation of momentum applied to the Compton effect shown in the diagram above.
 Self-Check Answer
Self-Check Answer
SC 1.
The photon with a wavelength of 2 nm will have the larger momentum because momentum is inversely proportional to wavelength.
SC 2.
The Compton Equation
As noted above, the change in wavelength of the incident photon varies depending on the scattered angle. Using algebra and Einstein’s theory of relativity, the Compton scattering can be analyzed mathematically with the following equation.
The change in wavelength of the X-ray before and after the collision is related to the angle at which it scatters. |
|||||||||||||||
|
 Watch and Listen
Watch and Listen
Open Compton Effect to see a demonstration of Compton's work.
 Read
Read
Read “The Compton Effect” on pages 721–725 of your physics textbook.
 Try This
Try This
TR 1. Complete “Practice Problems” 1 and 2 on page 723 of your physics textbook.
TR 2. Complete “Practice Problem” 1 on page 724 of your physics textbook.
Energy of a Photon
So far you've been working with two forms of the equation to find a photon’s energy: ![]() and
and ![]() . By rearranging the momentum formula above, you now have a third equation for a photon’s energy:
. By rearranging the momentum formula above, you now have a third equation for a photon’s energy: ![]() , where p is the momentum of the photon in kg•m/s and c is the speed of light in a vacuum.
, where p is the momentum of the photon in kg•m/s and c is the speed of light in a vacuum.
Conservation of Energy
The collision observed in Compton’s experiment is perfectly elastic, so the kinetic energy is conserved.
Recall: Most collisions observed in real life are not perfectly elastic. In these collisions some of the initial kinetic energy is transformed into other forms, such as heat and sound. In collisions that are not perfectly elastic, Ek final < Ek initial.
The kinetic energy of the incident X-ray photon is equal to the kinetic energy of the scattered X-ray photon plus that of the recoil electron. |
|||||||||||||||
|
 Try This
Try This
TR 3. Complete “Practice Problem” 3 on page 723 of your physics textbook.
 Module 6: Lesson 3 Assignment
Module 6: Lesson 3 Assignment
Remember to submit your answers to A 1, A 2, A 3, and A 4 to your teacher as part of your Module 6: Lesson 3 Assignment.
A 1. What is the difference between the photoelectric effect and the Compton effect?
A 2. How does the Compton effect show the wave-particle duality of light?
A 3. An X-ray with a frequency of 3.74 × 1020 Hz is incident on a thin piece of metal. The lower frequency X-ray on the other side is observed deflected at 48°. What is the frequency of the deflected X-ray?
A 4. The scientist changes the frequency of the incident X-ray to 4.50 × 1020 Hz and measures the deflected X-ray frequency of 4.32 × 1020 Hz. What is the angle of deflection?
1.14. Page 3
Module 6—Wave-Particle Duality and Quantum Physics
De Broglie’s Wave Equation
The photoelectric effect and the Compton effect both demonstrate the particle characteristics of a photon supporting the notion of wave-particle duality. A natural consequence of this is to ask if a particle, such as an electron, could behave like a wave. Louis de Broglie introduced this idea in 1923. He proposed, based on Compton’s findings, that matter-possessing momentum has a characteristic wavelength according to ![]() .
.
For an electron travelling near the speed of light, this equation becomes ![]() .
.
The first evidence of matter waves came several years later when physicists C.J. Davison and L.H. Germer accidentally discovered that a beam of electrons can create an interference pattern. Ultimately, this discovery contributed to the development of the modern electron microscope.
 Watch and Listen
Watch and Listen
Open “de Broglie Waves” to see a demonstration of de Broglie's work.
 Read
Read
© Musem of Science, Boston
Read “Then, Now and Future, The Electron Microscope” on page 727 and “De Broglie’s Wave Hypothesis: Strange but True!” on page 729 of your physics textbook.
As you discovered in the reading about electron microscopes, the magnification of a microscope depends on the inverse of the wavelength that produces the image. The electron microscope is able to generate matter waves with wavelengths much smaller than that of visible light, leading to greater magnification as you can see in the picture of the fly’s eye to the right.
Example Problem 1. What is the wavelength of an electron with a speed of 5.50 × 106 m/s? How many times smaller is this wavelength compared to a 400-nm red light?
Hint: When asked to compare two quantities, answer by stating how many times larger or smaller one quantity is relative to the other.
Given
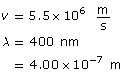
Required
the wavelength of the electron and the ratio of the wavelengths of the electron and red light
Analysis and Solution
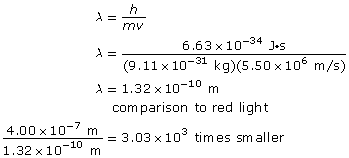
Paraphrase
The wavelength of the electron is 1.32 × 10–10 m, and it is 3.03 × 103 times smaller than the wavelength of red light.
Example Problem 2. What is the wavelength of an electron that has a kinetic energy of 3.10 × 10–16 J?
Given
![]()
Required
the wavelength of the electron
Analysis and Solution
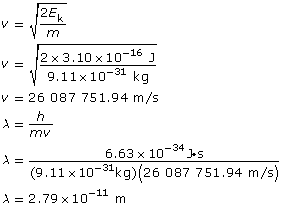
Paraphrase
The wavelength of the electron is 2.79 × 10–11 m.
 Self-Check
Self-Check
SC 3. What is the wavelength of an electron that has a speed of 2.25 × 107 m/s?
SC 4. What is the wavelength of an electron that has a kinetic energy of 7.5 × 10–4 MeV?
SC 5. What is the speed of an electron that has a wavelength of 7.00 pm?
SC 6. What is the wavelength of an electron that is accelerated from rest through a potential difference of 1000 V?
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 3.
Given
![]()
Required
the wavelength of the electron
Analysis and Solution
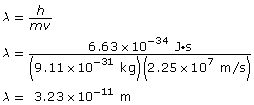
Paraphrase
The wavelength of the electron is 3.23 × 10–11 m.
SC 4.
Given
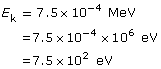
Required
the wavelength of the electron
Analysis and Solution
Change the energy in eV to J
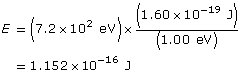
Use the kinetic energy to find the velocity.
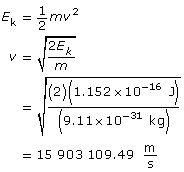
Use the velocity to find the wavelength.
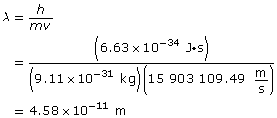
Paraphrase
The wavelength of the electron is 4.58 × 10–11 m.
SC 5.
Given
![]()
Required
the velocity of the electron
Analysis and Solution
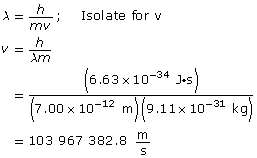
Paraphrase
The speed of the electron is 1.04 × 108 m/s.
SC 6
Given
V = 1000 V
Required
the wavelength of the electron
Analysis and Solution
Calculate the change in energy (or work done) of the electron.
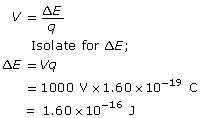
Calculate the velocity using ![]() .
.
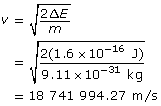
Calculate the wavelength.
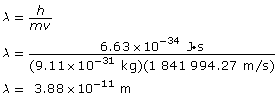
Paraphrase
The wavelength of the electron is 3.88 × 10–11 m.
 Read
Read
Heisenberg’s uncertainty principle: a principle stating that it is impossible to know both the position and momentum of a particle with unlimited precision at the same time
Read “De Broglie’s Hypothesis—A Key Concept of Quantum Physics” and “Heisenberg’s Uncertainty Principle” on pages 730 to 735 of the textbook.
 Module 6: Lesson 3 Assignment
Module 6: Lesson 3 Assignment
Remember to submit your answers to A 5, A 6, A 7, and A 8 to your teacher as part of your Module 6: Lesson 3 Assignment.
A 5. How did de Broglie’s wave equation show that energy and matter are similar?
A 6. A stationary hydrogen atom with a mass of 1.67×10-27 kg absorbs a photon of light with 10.2 eV. What is the velocity of the hydrogen atom after absorbing the photon in a perfectly inelastic collision?
A 7. If you performed Young’s experiment with high-speed electrons instead of light, what would the results look like? How does this support the wave or particle model?
A 8. What does Heisenberg’s uncertainty principle mean about physicists’ attempts to measure the size of the electron?
 Discuss
Discuss
De Broglie’s wave equation takes a simple mathematical form. His theory that a moving particle is associated with a wavelength, however, leads to some very interesting conclusions. For example, using the wave nature of particles and the concept of standing wave patterns, it is possible to explain why an electron can only have specific amounts of energy.
Based on these readings, answer the following:
D 1. Explain why a “particle in a box” can only have certain amounts of energy. Post your solution in the discussion area.
 Module 6: Lesson 3 Assignment
Module 6: Lesson 3 Assignment
Remember to submit your answer to D 2 to your teacher as part of your Module 6: Lesson 3 Assignment.
D 2. Read the solutions that two other students have posted. Use what you learn from their solutions to improve your own. Include comments on what you learned from the other two submissions.
Discussion Scoring Guide
Principles involved: Wave nature of matter, Heisenberg’s uncertainty principle |
||||
Criteria |
Level 1 (Below Standard) |
Level 2 (Approaching Standard) |
Level 3 (Standard) |
Level 4 (Above Standard) |
Knowledge |
||||
Demonstrates understanding of the situation, physics principles and technology, and their connections. |
Demonstrates a vague and sometimes incorrect understanding of the physics principles involved. Obvious irrelevant or missing information. |
Demonstrates a basic understanding of the physics principles involved. May exhibit minor mistakes or vague information or application to the situation. |
Demonstrates a good understanding of the physics principles involved and applies them properly to the given situation. All necessary information is given. |
Demonstrates a superior understanding of the physics principles involved and their application to the situation. All applications are considered in detail. |
Reflection |
||||
The post shows reflection on one’s own and other students’ work. Contributes to the group discussion. |
Does not make an effort to participate. Seems indifferent to discussion. | Occasionally makes meaningful reflections on the group’s efforts or discussions. Marginal effort is shown to become involved with the group or discussion. | Frequently makes meaningful reflections on the group’s efforts and presents relevant viewpoints for consideration by the group. Interacts freely with group members. | Regularly attempts to motivate the group discussion and delve deeper into concepts. Interacts freely and encourages all group members. |
Content and presentation of discussion summary |
||||
The information is logically arranged in a clear and concise manner. |
The information is poorly organized with many concepts implied. Irrelevant or rambling sentences make reading difficult. | The information is somewhat organized with implied concepts. Excessive words or awkward sentences are used, which hinder reading. | The information is well-organized and logically arranged. All concepts are explicitly explained. There are a few awkward but understandable sentences. | The information is well-organized and very easy to understand. Well-worded sentences make reading pleasurable. |
1.15. Page 4
Module 6—Wave-Particle Duality and Quantum Physics
 Reflect and Connect
Reflect and Connect
Quantum physics and theory related to wave-particle duality has produced amazing technologies, like the electron microscope, while helping to explain the nature and behaviour of electromagnetic radiation. Yet, the precise answer to the age-old question, “what is light?” still remains. Perhaps the lack of a clear answer means that it is not a realistic question. The science simply reveals a duality—a reality that is accepted, rejected, or modified with new discoveries and insight.
Young’s double-slit experiment is a case in point. The classic two-slit interference pattern (studied in Module 5: Lesson 6) can be formed in very strange ways. For example, if only one photon of light is directed at two slits, it will go through one or the other opening forming a dot on the screen. Then another photon passes through one of the openings, again forming another dot on the screen. Over time an interference pattern forms, even when only one photon at a time is allowed to pass through. You can see this in Figure 14.29 on page 738 in your textbook. The photons interfere constructively and destructively, even though they do not pass through the slits at the same time. It is a very strange idea that, somehow, each photon is aware of the photons that came before!
 Read
Read
You may explore this and other strange consequences of wave-particle duality by reading “Coming to Terms with Wave-particle Duality and the Birth of Quantum Mechanics” on pages 737 to 740 of your physics textbook.
From its birth in the early 1900s, quantum theory continues to evolve. Today, quantum theory is used in the production of all electronics—cell phones, flat screen TVs, mp3 players, computers, GPS navigation, car engine monitoring computers, etc. Even though the majority of people do not know or understand quantum theory, it is a cornerstone of our modern life and affects much of what we do daily and will continue to help shape the technology of tomorrow.
 Module 6: Lesson 3 Assignment
Module 6: Lesson 3 Assignment
Remeber to submit the Module 6: Lesson 3 Assignment to your teacher.
1.16. Page 5
Module 6—Wave-Particle Duality and Quantum Physics
 Lesson Summary
Lesson Summary
In this lesson you focused on the following questions:
- What is the Compton effect and how is it related to the conservation of energy and momentum?
- How does the Compton effect support wave-particle duality?
- If light can behave as a particle, can a particle behave as a wave?
- What is de Broglie’s wave equation?
The Compton effect is an increase in wavelength, hence a decrease in energy, of an X-ray as a result of its interaction with matter. Compton observed the energy and momentum of the incident X-ray, the scattered X-ray, and the electron it collided with. He discovered that the collision demonstrated the conservation of momentum and energy, just as it would for an elastic collision between two particles. Thus, the Compton effect provides supporting evidence for the particle nature of EMR.
The de Broglie wave equation is based on the Compton effect and predicts that any particle that possesses momentum will have a characteristic wavelength according to
Lesson Glossary
Compton effect: an increase in wavelength of an X-ray as a result of its interaction with matter
Compton scattering: the scattering of an X-ray when it interacts with an electron
Heisenberg’s uncertainty principle: a principle stating that it is impossible to know both the position and momentum of a particle with unlimited precision at the same time
1.17. Module Summary/Assessment
Module 6—Wave-Particle Duality and Quantum Physics
 Module Summary
Module Summary
In Module 6 you learned about the evidence related to the quantum model and wave-particle duality in relation to blackbody radiation and the photon as a quantum of EMR, the photoelectric effect and the conservation of energy, and the Compton effect and the conservation of momentum and energy.
In Lesson 1 you learned about the quantum and how it relates to blackbody radiation. Blackbody radiation refers to a hypothetical object that absorbs all of the electromagnetic radiation that falls on it. The intensity and wavelength (or frequency) of the emitted radiation can be used to construct a blackbody radiation curve. Attempts to explain these curves using classical physics gave nonsensical solutions. Planck was able to explain the blackbody radiation curves by assuming that energy is emitted from hot objects in discrete bundles, or photons, each capable of transferring a minimum quanta of energy associated with its wavelength and frequency according to Planck’s formula, E = hf.
You also learned that for physics in general, the idea of the quantum marked the end of classical physics and the beginning of quantum physics by showing that light could be considered a photon, a particle.
In Lesson 2 you examined the photoelectric effect experiment and how it supports wave-particle duality. The photoelectric effect showed that light above a threshold frequency is able to cause a potential difference across a metal plate. Einstein explained this effect by using Planck’s quantum hypothesis. Einstein proposed that the energy delivered by a single incident photon is defined by Planck’s formula and that a certain amount of energy, called the work function, is required to free an electron from a metal surface. According to the conservation of energy principle, any extra energy from the photon is contained in the motion of the photoelectron as it leaves the metal surface. These relationships were then verified by Millikan’s experiments using stopping voltage to measure accurately the kinetic energy of the photoelectrons.
This gave evidence for Planck’s hypothesis and the particle nature of light. As the wave nature was clearly shown in Unit C, the new theory combined both into the wave-particle duality of light.
In Lesson 3 you learned about the Compton effect and how it was explained using conservation momentum and energy. When Compton shone an X-ray on a sheet of metal, he observed that the X-ray’s wavelength increased (decreased in energy). He investigated the lost energy and discovered that electrons were ejected from the metal plate. He analyzed the results and saw that energy was conserved but was surprised to see that momentum was also conserved. This gave further supporting evidence for the wave-particle duality.
As many physicists were observing the wave-particle duality as it applied to light, de Broglie looked at the wave properties of particles, specifically electrons. He mathematically predicted that high-speed particles would exhibit wave-like properties. His prediction was verified by the electron wave interference, accidentally observed by Davisson and Germer who received the Nobel Prize for the discovery of “matter waves” in 1937. The de Broglie wave equation also explains the quantization of electron energy using resonance and wave interference in a confined space, further supporting quantum theory.
All of the concepts presented in this module were designed to help you understand wave-particle duality and quantum theory. In the next module you will see how nuclear reactions in the nuclei of atoms reveal further information about the atom and the fundamental forces that govern the nature of matter.
Module Assessment
As your module assessment do the following two questions. The first is a holistic question, and the second is a vector question.
Question 1
Use the following information to answer this holistic question.
The labels have fallen off two evacuated quartz tubes that have unknown metals at each cathode. One evacuated quartz tube, with Metal X as its cathode, detects visible light leakage from cameras. The other evacuated quartz tube, with Metal Y as its cathode, detects ultraviolet leakage from shielded equipment. A student needs to know which evacuated quartz tube has Metal X and which has Metal Y. The following is one of the evacuated quartz tubes.
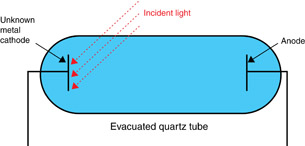
Also available for your experiment are a variable-frequency electromagnetic wave source, a variable voltage source, a voltmeter, and any reference tables needed.
Design an experiment using the photoelectric effect to distinguish between Metal X and Metal Y. Your experimental design must contain the following components:
- statement of the purpose of the experiment
- list of the equipment needed
- completely labelled diagram of all the equipment necessary
- procedure
- measurements to be made and recorded and any tables necessary
- description of the analysis
- explanation using either the calculation or the derived algebraic equation showing how it will be used to distinguish between Metal X and Metal Y
Question 2
Use the following information to answer the following question.
A university professor is setting up an example for a class of students. The professor wants to demonstrate Compton scattering of electrons. The professor uses an X-ray machine to project an X-ray with a wavelength of 1.38 × 10–11 m at a thin metal sample. The professor finds that the scattered X-rays have a wavelength of 1.54 × 10–11 m.
Determine the
- angle at which the X-rays scatter
- velocity of the ejected electrons (speed and direction), assuming that they start at rest (Ignore any relativistic effects.)
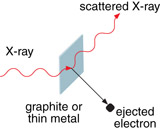
1.18. Module Glossary
Module 6—Wave-Particle Duality and Quantum Physics
Module Glossary
blackbody: any object that absorbs all EMR that falls on it and is capable of being a perfect emitter, releasing energy in the form of EMR
blackbody radiation curve: a graph of the intensity of EMR versus wavelength for an object at a given temperature
Compton effect: an increase in wavelength of an X-ray as a result of its interaction with matter
Compton scattering: the scattering of an X-ray when it interacts with an electron
Heisenberg’s uncertainty principle: a principle stating that it is impossible to know both the position and momentum of a particle with unlimited precision at the same time
incandescent: glowing with heat
quantum (pl. quanta): the smallest bundle or packet of energy that a given wavelength or frequency of EMR can possess
photoelectric effect: the emission of electrons when a metal is illuminated by EMR with a frequency greater than or equal to the metal’s threshold frequency
photoelectron: an electron emitted from a metal because of the photoelectric effect
photon: one quantum of light
Planck’s formula: EMR energy is the product of the number of quanta, Planck’s constant, and the frequency of the radiation
stopping voltage: the potential difference for which the kinetic energy of a photoelectron equals the work needed to move through a potential difference
threshold frequency: the minimum frequency that a photon can have to cause photoemission from a metal
wave-particle duality: the notion that EMR has both wave-like and particle-like characteristics
work function: the minimum energy that a photon can have to cause photoemission from a metal
Each metal has a specific work function.