Lesson 2. Concentration of Ionic Solutions
| Site: | MoodleHUB.ca 🍁 |
| Course: | Chemistry 20 BOOTSTRAP EXAMPLE |
| Book: | Lesson 2. Concentration of Ionic Solutions |
| Printed by: | Guest user |
| Date: | Sunday, 7 December 2025, 4:37 PM |
Description
.
1. Ionic Solutions and Dissociation
Dissociation of Ionic Compounds
In the previous lesson, we studied molarity, dilution, and steps in preparing solutions. In these lessons, we will expand on these concepts.
Ionic compounds are created by the mutual attraction of positively charged ions called cations, and negatively charged ions called anions. Structurally, ions differ from atoms as a result of having more or fewer electrons than protons in the orbitals about the nucleus. Having more electrons than protons results in a negative net ionic charge, and a positive net ionic charge is generated when protons outnumber electrons. An ionic compound is electrically conductive as a result of these electron imbalances. Positive and negative ionic charges cause ions from structures through which a current of electrons can flow across all of the positive and negative pathways between ions, particularly when in solution.
Why the ionic solutions are electrolytic while molecular solutions are not?
Study the following two models: 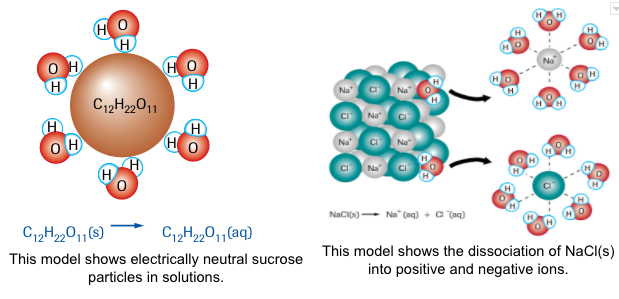
Key Concepts
Dissociation
Concentration of ions
Solubility
Dynamic equilibrium

Learn more go to Textbook p. 192-214
While the first model shows the neutral sucrose molecules surrounded by water molecules, the second model shows that NaCl dissolves and forms positive ions that surrounded by the negative ends of the polar water molecules and the negative ions are surrounded by the positive ends of the polar water molecules. The separation of ions in ionic solution is called dissociation. The equation below shows the dissociation of NaCl;
NaCl(s) --> Na+(aq) + Cl-(aq)
Another example, (NH4)2SO4(s) --> 2NH4+(aq) + SO42-(aq)
Notice that both equations do not show H2O(l) as a reactant in the equation. Water as a solvent is necessary for the process of dissociation. However, it is not consumed and therefore is not a reactant. The presence of water molecules surrounding the ions is indicated by (aq).
2. Ionization
Ionization
Earlier, we talked about ions produced via dissociation which refers to the separation of ions that are present in ionic compounds. Now, we will study the concept of ionization which refers to the reaction in which the polar covalent compounds are converted into ions in water.
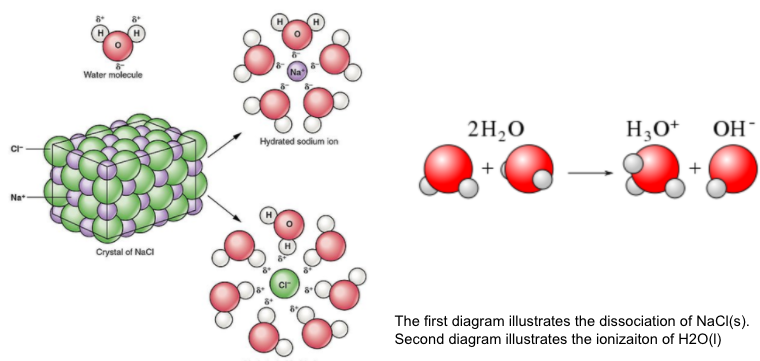
When molecular solute ionizes in solution the molecular solute reacts with the solvent (water) to form ions not present in the original molecule. The best example of ionization can be seen in strong and weak acids and bases.
HCl(aq) + H2O(l) --> H3O+(aq) + Cl-(aq)
NH3(g) + H2O(l) --> NH4+(aq) + OH-(aq)
In both examples, none of the ions formed existed in the original solute of HCl and NH3. We use dissociation and ionization equations to calculate the concentration of individual ions in solution. In a balanced equation, the coefficients of the ions produced in solution will give us ratios of concentration relative to the concentration of the solute.
Example 1
What is the concentration Na+(aq) and PO43- in a solution of 0.600 mol/L Na3PO4(aq)?
Solution
Step 1: Write a balanced dissociation equation.
Na3PO4(s) --> 3Na+(aq) + PO43-(aq)
From the equation, there will be 3 moles of Na+ for every 1 mole of Na3PO4(s).
Step 2: Calculate the concentration of Na+(aq) and PO43-(aq). Use square brackets to represent the concentration
[Na+(aq) = 3x 0.600 mol/L = 1.800 mol/L
[PO43-(aq)] = 1x 0.600 mol/L = 0.600 mol/L
Example 2
Determine the amount concentration of barium and hydroxide ions in a solution made by dissolving 5.48 g of barium hydroxide to make a volume of 250 mL.
Solution
Step 1: Write a balanced ionization reaction, and list givens
Ba(OH)2(aq) --> Ba+(aq) + 2OH-(aq)
5.48g
171.35 g/mol (molar mass)
250 ml= 0.250 L
Step 2: calculate moles: molar mass of barium hydroxide: 171.35 g/mol
n = 4.48g x 1mol/ 171.35 g = 0.032 mol Ba(OH)2
C= n/ V = 0.032/ 0.250 = 0.128 mol/L
Step 3: Use mole ratio which is (coefficients) to determine the concentration
Ba(OH)2(aq) --> Ba+(aq) + 2OH-(aq)
1 mol/L 1 mol/L 2 mol/L
0.128 mol/L 0.128 mol/l 0.256 mol/L
3. Solubility and Saturated Solutions
Solubility
Solubility is the amount of a solute that dissolves in a given volume of solvent. It is usually recorded in g/100 mL.
How Temperature affects Solubility:
- Solubility of solids in liquids increases with temperature
- Solubility of liquids in liquid is unaffected by temperature
- Solubility of gases in liquids decreases with temperature
How Solubility affects Solubility:
- Solubility of gases in liquids increases as the pressure of the gas above the solution increases
- Solubility of solids in liquids is unaffected by a change in pressure
Substances that mix completely with each other in all proportions are said to be miscible. Miscibility depends on the nature of the solute and solvent. In general, polar solutes dissolve well in polar solvents, non-polar solutes dissolve well in nonpolar solvents. Probably you've heard the phrase 'Like dissolves like' before.
There are exceptions to the 'like dissolves like' rule as some ionic compounds are either insoluble in water or only slightly soluble. The solubility table is used to predict the solubility of an ionic compound in water. Examine the solubility table in the back of your textbook, then watch the video below.
Saturated Solutions
A saturated solution is a solution that contains both dissolved solute and undissolved solute. It is a solution said to have its maximum concentration of solute dissolved at a given temperature. Dissolving has not stopped in the solution because the solution is at equilibrium. The same amount of solute remains undissolved as solute continues to dissolve and crystalize out at the same rate. This is one type of dynamic equilibrium. At dynamic equilibrium reaction is two-directional. Example: ![]()
The solubility of a solute is best determined when it is a saturated solution.
4. Preparing Solutions
The preparation of a solution is a lab procedure that should be learned. Although you will not bet the opportunity to do this at home, you are expected to learn the procedures.
Steps involved in preparing a solution:
1. Calculate the mass required.
2. Measure out the mass on a scale
3. Place the solid in a clean dry beaker
4. Dissolve the substance in about 1/2 of the final volume
5. Transfer the solution to a volumetric flask.
6. Rinse all equipment with distilled water
7. Use a medicine dropper to bring the volume up the line on the flask. The bottom of the meniscus should be on the line.
8. Stopper the flask and invert several times.
Example:
Prepare 100 mL of a 0.100 M (mol/L) solution of sodium carbonate.
Materials:
solid sodium carbonate, 100 mL beaker, scale, scoopula, stopper, funnel, stir rod, a medicine dropper
Procedure:
1. Calculate the mass
n= CV= 0.100M x 0.100 L = 0.0100 mol
The molar mass of NaCO3 is 105.99 g/mol
m= nM = 0.0100 mol x 105.99 g/mol
m=1.0599 g
2. Place the beaker on the scale, push the tare button to zero the scale with the beaker on it. Measure out 1.06 g
3. Pour about 50 mL of distilled water into the beaker. Stir with a stir rod until all of the solid is dissolved.
4. Using a funnel, transfer the solution to the volumetric flask. Rinse the beaker and stir rod and funnel with distilled water.
5. Bring volume up to the line using a medicine dropper
6. Stopper the flask and invert at least twice.