Module 1
| Site: | MoodleHUB.ca 🍁 |
| Course: | Biology 30 [5 cr] - AB Ed copy 1 |
| Book: | Module 1 |
| Printed by: | Guest user |
| Date: | Thursday, 18 September 2025, 4:30 PM |
Description
Created by IMSreader
Table of contents
- 1. Module 1
- 1.1. Lesson 1
- 1.2. Page 2
- 1.3. Page 3
- 1.4. Page 4
- 1.5. Page 5
- 1.6. Lesson 2
- 1.7. Page 2
- 1.8. Page 3
- 1.9. Page 4
- 1.10. Page 5
- 1.11. Lesson 3
- 1.12. Page 2
- 1.13. Page 3
- 1.14. Page 4
- 1.15. Page 5
- 1.16. Lesson 4
- 1.17. Page 2
- 1.18. Page 3
- 1.19. Page 4
- 1.20. Page 5
- 1.21. Lesson 5
- 1.22. Page 2
- 1.23. Page 3
- 1.24. Page 4
- 1.25. Page 5
- 1.26. Module 1 Summary
1. Module 1
Module 1: The International System of Units (SI)
Module 1 Introduction

© Copyright © BIPM Reproduced with permission.
The photograph you see shows the International Bureau of Weights and Measures in Sévres, near Paris, France. This is the headquarters where representatives from around the world meet to set standards that affect the way people take and report measurements, both in science and in their daily lives.
These standards, called the International System of Units (le Système international d’unités), include metres, litres, and kilograms, which you may already be familiar with. This system is often referred to by its abbreviation, SI. You may also know this system by its other name—the metric system.
The SI has its origins in France. The system arose as an effort to standardize and simplify measurements after the French Revolution. Today, the SI (or the metric system) is commonly used in the majority of countries around the world.
In Canada, the metric system was legalized in 1871, although the imperial system of measurement (feet and pounds) continued to be widely used until the second half of the twentieth century. Even today, there are many people who think of their height and weight in feet and pounds rather than in centimetres and kilograms. Do you?
In this module you will explore the following question:
What is the International System of Units (SI), and how is it used to measure length, area, volume, mass, and temperature?
Once you have completed this module, you should have the necessary skills to complete the first half of the Unit 1 Project.
Save a copy of the Module 1 Glossary in your course folder now. The Module 1 Glossary is a list of all of the new terms you will see in the lessons. Each time you see a definition, open your copy of the Glossary. Use the space available to add notes or drawings to help your understanding. You will be able to use your personal Glossary as a study tool.
1.1. Lesson 1
Module 1: The International System of Units (SI)
Lesson 1: Length
Focus

© Christopher Dodge/shutterstock
Anna is helping her father work on the family car.
“I think we’ll need the 10-mm metric wrench to loosen this bolt,” Anna observed.
“You’re right,” her father smiled. “How did you know?”
“Well, the hexagonal head of the bolt is about the width of my small finger. And that’s about 1 cm, or 10 mm!”
Metric wrenches, such as the one in the photograph, are sized in millimetres. Do you remember how to convert millimetres to centimetres? What would a 12-mm wrench be in centimetres? What would it be in metres?
Lesson Questions
In this lesson you will explore these questions.
- How is length measured in SI?
- What are the common units used when measuring length in SI?
- How are lengths in one unit converted to another unit?
Assessment
You will complete the Lesson 1 Assignment Booklet for assessment. Download the Lesson 1 Assignment Booklet and save it in your course folder now. You will receive instructions on how to complete the Assignment Booklet later in the lesson. You will also be prompted to start working on the Unit 1 Project.
There are other activities that you will complete throughout this lesson. It is important to complete all activities and save them in your course folder. Your teacher may ask to see your work at any time.
The lesson provides you with opportunities to investigate, review examples, and practise the knowledge and skills you are learning. In Self-Check activities you can compare your answers to see if you are on track. If you are having difficulty with concepts or calculations, contact your teacher.
Required Materials and Equipment
To complete this lesson you will need the following items:
- a metric (SI) ruler or metre stick
- a metric (SI) tape measure
1.2. Page 2
Module 1: The International System of Units (SI)
Get Started
Imagine you are in a corral putting a saddle on your favourite horse. Suppose you didn’t have a ruler, tape measure, or any other measuring device. How might you tell a friend how tall your horse is? You might use the width of your hand to measure how tall the horse is. In fact, some people describe horses’ heights using the term hands.
Parts of your body can be used to measure objects. You could use the width of a finger or the width of your hand, or you might use the length of your arm. Can you suggest a measure you could use to describe the distance from your home to your friend’s home?
 Try This
Try This
If possible, work with a partner to complete this activity. You will measure the length of a variety of objects using parts of your body.
Step 1: Prepare a table with three columns. Place the title “Object” in the first column. Title the second column “My Measurement,” and the third column “Partner’s Measurement.”
Step 2: Identify parts of your body that could be used to measure the length of objects around you. These may include the width of your fingers or hands, arm lengths, or paces.
Step 3: Identify objects around you that can be measured using the body part measures identified in Step 2. List these in the first column of your table. Your list may include objects like the width of a door, the length of a kitchen table, the length of a wall, or the height of a water glass.
Step 4: Measure the objects you listed in Step 3 using an appropriate body part measure. Record your measurement in the second column of your table. Have your partner repeat the measurement. Record your partner’s measurement in the third column of your table.
Use the data in your table to answer the following questions.
TT 1. Review the measurements recorded in your table. Were the measurements recorded by you and your partner identical?
TT 2. Suggest a reason for similarities, or lack of similarity, between the measurements made by you and your partner.
Place a copy of your answers in your course folder. Your teacher may look at your work in order to monitor your learning.
A Standard Unit of Length
metre: the base unit of length (or linear measure) in SI
Remember to open the Module 1 Glossary that you saved in your course folder at the start of Module 1, and then add any notes that will help you understand the definition for metre. Forgot to save the document? You can download the Module 1 Glossary from the Toolkit.
You may have observed that using a measurement system that relies on body parts does not always allow for consistent measurement. SI provides a standard length called the metre, so two people measuring independently will obtain the same measures of length and distance.
For small lengths, the metre is divided into smaller parts using powers of 10. You will encounter decimetres, centimetres, and, millimetres which are tenths, hundredths, and thousandths of a metre. Similarly, for longer distances, 10 times, 100 times, and 1000 times a metre are common.
Each of the SI units of length relate to the others by a power of 10. That is why one of the skills you will need to work in SI is multiplying and dividing by powers of 10.
 Try This
Try This
Use “Powers of 10” to review the powers you will need to understand SI.
When you’ve launched this multimedia piece, drag the slider one way and then the other. When the exponent of 10 is positive, see how the exponent relates to the number of instances 10 appears as a factor in the expanded form and the number of zeroes in the product. When the exponent is negative, see how the exponent relates to the number of zeroes in the product.
 Self-Check
Self-Check
SC 1. Create a table like the one below and complete it. Use “Powers of 10,” which you used in the Try This activity, to check your answer.
| Powers of 10 in Standard Form | Powers of 10 in Exponent Form |
| 1000 | 10 × 10 × 10 = 103 |
| 100 | |
| 10 | 101 |
| 1 | |
| 0.1 | |
| 0.01 | 10–2 |
| 0.001 |
Multiplying Powers of 10
Do you remember the shortcut or rule for multiplying by a power of 10? Suppose you had to multiply 17.54 by 102. Following the shortcut, you would simply move the decimal place to the right 2 places. You move the decimal place 2 places, because the exponent of 10 is 2, and you move to the right because the exponent is positive.
To practise this shortcut, go to “Multiplying Powers of 10.”
There are two sliders. The left slider allows you to enter a number from zero to 100. The other slider allows you control the value of the exponent in the power of 10. Pay special attention to what happens to the decimal when you multiply by a power of 10 having a negative exponent. You can also enter values directly in the small box beside each slider.
 Self-Check
Self-Check
Complete the following questions using the shortcut for multiplying by powers of 10. You may use “Multiplying Powers of 10” to check your answers.
SC 2. What is 3.92 multiplied by 104?
SC 3.What is 9.9 multiplied by 10–5?
SC 4. 31.42 × 1000 =
Dividing Powers of 10
So, to multiply by a power of 10, move the decimal to the right or left depending on the sign of the exponent. If you multiplied a number by 0.0001, how far would you move the decimal and in which direction?
Do you remember the shortcut for dividing by powers of 10? What is 4.85 ÷ 1000?
Now you should be ready to begin the Explore. You just reviewed your skills with powers of 10. These skills will help you convert a measurement in one SI unit of length to an equivalent measurement expressed in another unit of length!
4.85 ÷ 1000 = 0.004 85. Because 1000 = 103, the decimal moves 3 places to the left. When dividing, the decimal moves in the opposite direction as it would when multiplying!
1.3. Page 3
Module 1: The International System of Units (SI)
Explore
In this activity you will explore how the metre and other SI units of measure can be used to describe everyday lengths, such as your height.
Have you ever considered expressing your height in millimetres or in metres? How might you make such a conversion? If you thought that such a conversion involves a factor of 10, you were on the right track. Complete the following Try This activity to learn about the SI unit for measurement, and how powers of 10 are involved in converting between its units.
 Try This
Try This
With a partner, measure each other’s height to the nearest tenth of a centimetre. Your partner may be a classmate, a friend, or a family member.
TT 3. Place your measured heights in a data table such as the following. Then express your heights in millimetres and in metres. Next, find the difference between your heights. Express that difference in centimetres, millimetres, and metres. Place your results in your data table.
|
Height |
Difference in Height |
||||
|
Measured |
Conversion |
Conversion |
Calculated |
Conversion |
Conversion |
|
cm |
mm |
m |
cm |
mm |
m |
|
You |
|
|
|
|
|
|
|
Partner |
|
|
|
|
|
|
As you complete the following questions, use your conversions and calculations from the chart to provide examples in your explanations.
TT 4. Explain how you would change a measurement in centimetres to millimetres and to metres?
TT 5. Explain how you would change a measurement in metres to centimetres and to millimetres?
 Share
Share
You are now going to be asked to share your answers to TT 1 to TT 5. Remember that sharing work is an important part of learning. Use the following tips to ensure you get all the benefits from this sharing opportunity:
- You have completed TT 1 to TT 5 to the best of your ability. The answers are in a form that allows you to share them easily with another student or with your teacher, if so directed.
- Use your class discussion area, or another method indicated by your teacher, to post your answers to TT 1 to TT 5 and to view the work of the people you are sharing with.
- Compare the answers for TT 1 to TT 5. Identify where you have similar answers, and where your answers are different. Discuss all differences between the answers until you have an agreement. If necessary, you may wish to involve your teacher in your discussion.
- Revise your answers to TT 1 to TT 5 where necessary.
Save the revised copy of your work to your course folder. Ask your teacher whether you are to save a transcript of your discussion in your course folder as well.
1.4. Page 4
Module 1: The International System of Units (SI)
Bringing Ideas Together
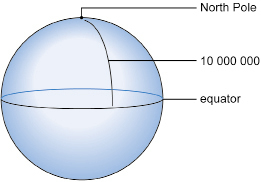
When SI was first developed in France over 200 years ago, the metre was defined as one ten-millionth of the distance from the North Pole to the equator.
Did You Know?
Today, because of the precision required in science and industry, the metre is defined as the distance light travels in a vacuum in the time interval of 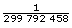 of a second.
of a second.
In SI, prefixes are used to represent multiples or fractions of the base unit.
- Add the prefix kilo to metre, and you have the kilometre.
- Add the prefix centi to metre, and you have the centimetre.
- Add the prefix milli to metre, and you have the millimetre.
The prefixes kilo, centi, and milli are the most common and are bolded, along with their symbols, in the following table of SI prefixes.
|
Prefix |
Symbol |
Factor |
|
mega |
M |
1 000 000 or 106 |
|
kilo |
k |
1000 or 103 |
|
hecto |
h |
100 or 102 |
|
deca |
da |
10 or 101 |
|
— |
— |
1 or 100 |
|
deci |
d |
0.1 or 10–1 |
|
centi |
c |
0.01 or 10–2 |
|
milli |
m |
0.001 or 10–3 |
|
micro |
µ |
0.000 001 or 10–6 |
 Try This
Try This
In comparing SI units to each other, the prefixes are important. Play “Prefix Matching Game” to help you quickly recognize and order the prefixes based on the factor they represent.
Prefixes in SI

© Stephen Coburn/shutterstock
For length, the most common prefixes you will generally encounter are milli, centi, and kilo. What are the symbols for millimetre, centimetre, metre, and kilometre? You may recall working with the symbols mm, cm, m, and km in previous math courses.
Have you seen the prefixes milli, centi, and kilo used with volume? In your course folder, record examples of these prefixes used to describe volumes you encounter during the day. In Lesson 3 you will explore volumes using these prefixes.
 Try This
Try This
In the Explore section of this lesson, you converted between SI units for measurement. This showed how powers of 10 are involved in converting between units. You must be able to convert quickly among these units by applying your skills with powers of 10.
Fortunately, because only powers of 10 are involved, SI unit conversion only involves the movement of the decimal. Open “SI Length Conversion” to see this conversion.
In this multimedia piece, drag the left slider, connected to a moveable box, up or down to match the units you have in a given measurement. Enter the numeric part of the measurement into the moveable box. Then drag the right slider to match the units into which you want to convert the measurement.
Still using “SI Length Conversion,” convert a distance of 500 m to kilometres (km). Using mental math, you may be able to predict that the conversion should show this measurement as 0.500 km. See that it does. Try several other conversions so that you are comfortable with this procedure.
TT 6. Make a rule that allows you to predict which direction you must move the decimal place when making unit conversions.
Write your rule in your course folder. Your teacher may look at your work in order to monitor your learning.
 Self-Check
Self-Check
SC 5. Complete a table like this one, then check your answers.
|
1 km = ? m |
1 m = ? km |
|
1 m = ? cm |
1 cm = ? m |
|
1 m = ? mm |
1 mm = ? m |
|
1 cm = ? mm |
1 mm = ? cm |

Estimating lengths and distances in SI is a useful skill. To estimate, it helps to visualize the size of some SI units. A millimetre is about the thickness of a dime, and a centimetre is about the width of your little finger. What everyday objects are about the length of a metre? A kilometre is the distance you can walk in about ten minutes.
Because you are working with powers of 10, you simply move the decimal point to convert between units. Work though several examples with your teacher or study partner.
Example 1

Coin image © 2010 Royal Canadian Mint – All Rights Reserved /
Image de pièce© 2010 Monnaie royale canadienne – Tous droits réservés
A two-dollar coin is approximately 28 mm in diameter.
- What is the width in centimetres (cm)?
- What is the width in metres (m)?
Solution
- Since 1 mm = 0.1 cm, multiply 28 mm by 0.1 or 10–1.

Can you suggest another way of doing the problem?

- Since 1 mm = 0.001 m, multiply 28 mm by 0.001 or 10–3.
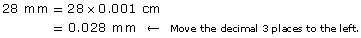
Example 2
Yin lives 2.5 km from school. Convert that distance to metres.
Solution
Since 1 km = 1000 m, multiply 2.5 km by 1000 or 103.

Example 3
Jon’s height printed on his driver’s licence is 162 cm. What is his height in metres?
Solution
Since 1 cm = 0.01 m, multiply 162 cm by 0.01 or 10–2.
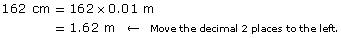
 Self-Check
Self-Check
SC 6. The local golf course is 6750 m in length. What is the length of this course in kilometres (km)?
SC 7. A roadside sign indicates a school-bus stop in 0.3 km. How far is the sign from the bus stop in metres?
SC 8. The length and width of a stamp are most often expressed in millimetres. Why?
SC 9. A package of 500 sheets of printer paper is 5 cm thick. How thick is a single sheet in metres?
SC 10.The height of the walls in Shawna’s room is 2.4 m. What is the height in centimetres?
SC 11. A letter-size sheet of copy paper is 216 mm by 279 mm. What are its dimensions in centimetres?
SC 12. Andrey Alexandrovich Silnov, of Russia, won the 2008 men’s high jump gold medal in the 2008 Olympics with a leap of 2.36 m. What was his achievement in centimetres?
SC 13. Inuit culture has existed since 1000 AD in Northern Canada and Alaska. The Inuit made toy sleds out of ivory and wood for their children. These toys taught their children about proper sled construction—a key skill in the frozen north!

What are the dimensions of the toy Inuit sled in millimetres?
SC 14. Anya, in Newfoundland, found an arrowhead from the Beothuks. Being curious, she researched her find and discovered it was not an arrowhead but the head of a sealing harpoon. Anya discovered that the Beothuks hunted seal by pursuing them in human-propelled boats (known as kayaks today). They made their catch by throwing harpoons (with rope attached) at their prey.

The harpoon head is made from flint and is 44.5 mm long. What is the length of this harpoon head in centimetres?
SC 15. The school running track is oval in shape and is 200 m in circumference. How many times must a runner go around the track to run 1.6 km?
 Mastering Concepts
Mastering Concepts
Try this question. When you are finished, check your answer.
The orbit of Earth around the sun is not circular. The distance from Earth to the sun changes as it travels around the sun. The closest Earth is from the sun is about 1.46 × 1011 m. The farthest Earth is from the sun is about 1.52 × 1011 m.
What is the difference between these distances in kilometres?
Express your answer in standard (everyday) notation. For example, 3.2 × 102 is a number in scientific notation. If instead of using 102, you move the decimal two places to the right, the result, 320, is in standard notation.
1.5. Page 5
Module 1: The International System of Units (SI)
Lesson Summary
Auto mechanics are skilled technicians who know the importance of choosing the right tool for the job. To choose the right tool, mechanics must be familiar with SI.

© Tselichtchev/shutterstock
In this lesson you explored three questions:
- How is length measured in SI?
- What are the common units used when measuring length in SI?
- How are lengths in one unit converted to another unit?
You discovered the metre is the base unit of length from which other units can be derived. You examined the relationships among the metre, millimetre, centimetre, and kilometre. You discovered these relationships are based on powers of 10. So, to convert among these units, you just move the decimal to the left or right. Look back to the chart of prefixes to review how each prefix relates to powers of 10 and affects the position of the decimal.
 Assignment
Assignment
Retrieve the Lesson 1 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment Booklet. Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Unit 1 Project
Before you move on to the next lesson, you should read through the Unit 1 Project and start thinking about what you may wish to do for the Project.
1.6. Lesson 2
Module 1: The International System of Units (SI)
Lesson 2: Area
Focus

© LightShaper/shutterstock
People modify the natural world. Some people live in communities with elaborate buildings. Other people create countless products for daily use. The habitat nature has provided for the bison doesn’t need modifications.
The bison is part of the natural landscape of the Canadian prairies. In the early 1800s, the bison’s range was from Mexico to Great Slave Lake in the Northwest Territories. Some estimates say there were as many as 50 million bison, or, on average, about one bison for every eight hectares of grasslands. The bison provided for many of the needs of First Nations and Métis peoples on the Great Plains.
Today you will often see bison as they graze on ranches and reserves. The number of bison that can graze on pasture of a given area depends on plants, rainfall, soil conditions, and climate. For example, suppose a reserve has 2 km2 of pasture available, and Elders estimate that each animal requires 2.5 ha (hectares). How many animals should be in the herd?
Lesson Questions
In this lesson you will explore these questions.
- How is area—the amount of surface—measured in SI?
- What are the common units used when measuring area in SI?
- How are areas in one unit converted to another unit?
Assessment
You will complete the Lesson 2 Assignment Booklet for assessment. Download the Lesson 2 Assignment Booklet and save it in your course folder now. You will receive instructions on how to complete the Assignment Booklet later in the lesson. You will also be prompted to start working on the Unit 1 Project.
Remember to save all activities, including those that are not part of the Assignment, in your course folder.
Required Materials and Equipment
To complete this lesson, you will need the following supplies:
- an old newspaper
- adhesive tape
- scissors
- a metric measuring tape or ruler
1.7. Page 2
Module 1: The International System of Units (SI)
Get Started

© Germán Ariel Berra/shutterstock
Suppose you wanted to describe the areas of a postage stamp, the front of your MP3 player, a living-room carpet, and a buffalo paddock. Could you use your thumbprints to describe the area of any of these?
For the carpet and the paddock, you would need an area unit much larger than a thumbprint. If you chose an appropriate area unit, you could cover the carpet or paddock with a specific number of area units that would be easy to express and understand.
 Try This
Try This
In this activity you will use your thumbprints to see how area units can be used to measure the area of a surface.
You will need a sheet of plain paper, like the paper you would use in a computer printer. In order to leave a record of your thumbprints, you will dip your thumb in cooking oil or a diluted mixture of food dye. You could also just use a pencil to outline the positions of your thumb on the sheet of paper.
Step 1: On your piece of paper, apply a method to give the approximate number of thumbprints you can fit on the sheet of paper.
TT 1. Approximately how many of your thumbprints cover the sheet of paper?
TT 2. Describe a method you used to find the approximate number of thumbprints you could fit on the sheet of paper.
TT 3. Based on your findings, what is the area of the sheet of paper in thumbprints?
Place a copy of your answers in your course folder.
Unit Squares
Your thumbprint is rounded and not square, so there is always some surface left uncovered between the thumbprints. You will remember from your earlier work that area is the number of unit squares needed to cover a surface. Unit squares can cover a surface without leaving any exposed space between the squares. That’s one reason why unit squares—rather than rounded unit shapes—are used to measure area.
Suppose a rectangular sheet is 4 units long and 3 units wide. A grid of lines is drawn over the sheet to make the dimensions and area visible. What is the area of this rectangular sheet?

How many unit squares cover this rectangle? Did you count the total number of squares, or did you remember a shortcut method based on multiplication?
Suppose a sheet is square, having a side length of 3 units. What is the area of this square sheet?
How can you use multiplication to determine the area of this square and any other square?
1.8. Page 3
Module 1: The International System of Units (SI)
Explore
You have seen that unit squares of various sizes can be used to measure area. SI provides units of area for many situations.
 Try This
Try This
In this activity you will explore common SI units of area and the relationships among them. Share your work from this activity and place it in your course folder.
You will need an old newspaper, tape, scissors, and a metric measuring tape or ruler.
Measure, cut, and tape some newspaper together to form a square that measures 1 m on each side—in other words, a 1-m square.

TT 4. Name three different surfaces you might measure using a 1-m square.
Next, from one corner of your 1-m square, cut a square that measures 1 cm on each side—in other words, a 1-cm square.

TT 5. Name three different surfaces you might measure using a 1-cm square.
TT 6. How many 1-cm squares could you cut from the 1-m square? How do you know?
Finally, from one corner of your 1-cm square, cut a square that measures 1 mm on each side—in other words, a 1-mm square.
TT 7. Name three different surfaces you might measure using a 1-mm square.
TT 8. How many 1-mm squares could you cut from the 1-cm square? How many 1-mm squares could you cut from the 1-m square? How do you know?
 Share
Share
It’s time to share your answers to TT 4 to TT 8. Remember that sharing work is an important part of learning. Use the following tips to ensure you get all the benefits from this sharing opportunity:
- You have completed TT 4 to TT 8 to the best of your ability. The answers are in a form that you can share easily with another student or with your teacher, if so directed.
- Use your class discussion area, or another method indicated by your teacher, to post your answers to TT 4 to TT 8 and to view the work of the people you are sharing with.
- Compare the answers for TT 4 to TT 8. Identify where you have similar answers, and where your answers are different. Discuss all differences between the answers until you have an agreement. If necessary, you may wish to involve your teacher in your discussion.
- Revise your answers to TT 4 to TT 8 where necessary.
Save the revised copy of your work in your course folder. Ask your teacher whether you are to save a transcript of your discussion in your course folder as well.
1.9. Page 4
Module 1: The International System of Units (SI)
Bringing Ideas Together
area: a measurement of how many square units a surface can be divided into
For example, if your living room carpet can be divided into 10 square metres, its area is 10 m2.
In the Explore section you worked with three common units of area in SI. They are the square metre (m2), the square centimetre, (cm2), and the square millimetre (mm2).
 Self-Check
Self-Check
From your work with the square metre, square centimetre, and square millimetre, you should now be able to complete the following question.
SC 1. In a table like the following, write your answers in two different ways—in standard form and as a power of 10. The first row is done for you as an example. Then check your answers.
|
SI Area Unit |
An Equal Area Using a Different Unit (Standard Form) |
An Equal Area Using a Different Unit (Powers of 10) |
|
1 m2 |
10 000 cm2 |
104 cm2 |
|
1 m2 |
? mm2 |
? mm2 |
|
1 cm2 |
? mm2 |
? mm2 |
 Read
Read
Because you are working with powers of 10, you simply move the decimal point to convert between units. Read and work through the following examples. To make the conversion from one area unit to another, you may use “SI Area Conversion.”
Example 1

© Canada Post Corporation {2009}. Reproduced with permission.
The dimensions of this stamp are 40 mm long × 31 mm wide.
- What is the area of the stamp in square millimetres (mm2)?
- What is the area of the stamp in square centimetres (cm2)?
Solution
- Since the stamp is a rectangle,
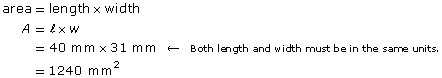
- Since 1 cm2 = 100 mm2 or 102 mm2, there will be fewer square centimetres. So, divide by 100, or 102.
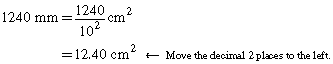
Another way to solve this problem is to change the dimensions to centimetres first.

Example 2
A bathroom mirror is 0.9 m long and 0.6 m wide.
- What is the area of the mirror in square metres?
- What is the area of the mirror in square centimetres?
Solution
- Since the mirror is a rectangle,
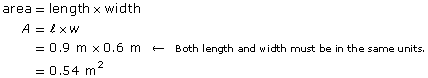
- Since 1 m2 = 10 000 cm2 or 104 cm2, there will be more cm2. So, multiply by 10 000 or 104.
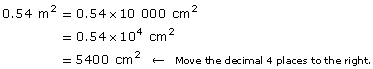
- Another way to solve this problem is to change the dimensions to centimetres first.
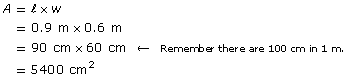
 Self-Check
Self-Check

© John Kroetch/shutterstock
Complete the following questions. In questions 1 and 2, do each conversion two different ways.You may use “SI Area Conversion” to help you.
SC 2. A Canadian flag on a post-office wall is 64 cm × 32 cm. What is the area in square centimetres and square metres?
SC 3. Measure the dimensions of a light-switch cover in your home. What is its area in square centimetres and in square millimetres? Why wouldn’t expressing the area in square metres be appropriate?
SC 4. What area unit would be the most appropriate for the area of a computer disk? Why?
SC 5. A sheet of computer paper is 216 mm × 279 mm. What is its area in square centimetres? Round your answer to one unit.
SC 6. Measure the dimensions of the floor in your bedroom. What is the area of your bedroom? Why did you choose the units you did?
Large Areas
For larger areas, such as the area of a province or the area of a grazing lease, two other SI units are commonly used. They are the square kilometre (km2) and the hectare (ha).

© 2009fotofriends/shutterstock
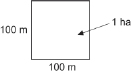
hectare: the area of a square 100 m on a side.
The symbol for one hectare is 1 ha.

A square kilometre is a square 1 km (1000 m) on each side. For example, the area of Wood Buffalo National Park, the largest national park in Canada, is 44 807 km2 in area. That area is just about the same as the area of a large square over 211 km on each side!
 Try This
Try This
If you have access to an open field at the corner of two roads that cross at right angles, start from the intersection and walk 100 paces (each about 1 m in length) along one road next to the field. Then turn into the field and walk 100 m parallel to the other road. Look back towards the intersection—the square you just paced off is close to 1 ha in area!
The Hectare
A hectare is approximately the area of a large football or soccer field.
How many hectares are in 1 km2?
Work through the following examples to practise using hectares and square kilometres.
Example 3
How many square metres are there in 1 ha?
Solution
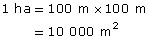
Example 4
A forest fire in northern Saskatchewan covered an area of 2000 ha. How many square kilometres did the fire cover?
Solution
There are 100 ha in 1 km2. So there would be fewer square kilometres than hectares. Divide the area in hectares by 100.
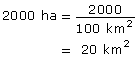
Example 5
A CFL football field is, with end zones and sidelines, about 137 m long and 59.5 m wide. What is its approximate area in hectares? Round your answer to one decimal place.
Solution
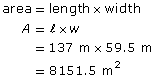
There are 10 000 m2 in 1 ha. So there would be fewer hectares than square metres. Divide the area in square metres by 10 000 ha.
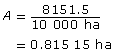
A CFL football field is about 0.8 ha.
 Self-Check
Self-Check
Do the following questions. When you are finished, check your answers.
SC 7. Stony Plain 135 is a reserve west of Edmonton that is home to the Enoch Cree Nation. Its area is 51.61 km2. What is the area of the reserve in hectares?
SC 8. Pacific Rim National Park, in British Columbia, covers 51 000 ha. What is its area in square kilometres?
SC 9. A quarter-section of land in Western Canada is a square about 804.7 m on a side. How many hectares does this area represent? Express your answer to the nearest unit.
SC 10. West Edmonton Mall covers an area of about 570 000 m2. How many hectares are in this area?
SC 11. At the turn of the century there was 1 bison, on average, for every 8.5 ha of grasslands on the Great Plains. How many square metres is 8.5 ha?
 Mastering Concepts
Mastering Concepts
Try this question. When you are finished, check your answer.
A certain rural road is 10 m wide. In paving a section of this road, a crew surfaced an area equal to 1 ha. What is the length of the newly paved section of road? Express your answer in metres.
1.10. Page 5
Module 1: The International System of Units (SI)
Lesson Summary

© Jeff Banke/shutterstock
Bison ranches are becoming more common across the Prairies. Ranchers need to determine how many animals the area they have for pasture can sustain. If you were a rancher, you would apply the skills you mastered in this lesson to manage your grazing land and your livestock.
In this lesson, you explored these questions.
- How is area—the amount of surface—measured in SI?
- What are the common units used when measuring area in SI?
- How are areas in one unit converted to another unit?
To answer these questions, you examined the relationships among the square metre, square centimetre, square millimetre, square kilometre, and hectare. You discovered these relationships are based on powers of 10. To convert among these units, you just had to move the decimal to the left or right.
 Assignment
Assignment
Retrieve the Lesson 2 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment Booklet. Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Unit Project
Before you move on to the next lesson, you should complete the scale diagram of your Unit 1 Project. Please note that when you complete your work later in this unit, you will be asked (at a later time) to indicate measurements using both SI and imperial units. Identify an area in your Unit 1 Project now that you will later convert to imperial measure. For more information about this and later steps in the Unit 1 Project, refer to the Unit 1 Project.
1.11. Lesson 3
Module 1: The International System of Units (SI)
Lesson 3: Volume and Capacity
Focus

© Jim Lopes/shutterstock
Will your Unit 1 Project involve using construction materials, such as concrete?
If you have helped plan or pour a concrete walk or driveway, you must be able to estimate accurately the volume of concrete you will need for the project in order to avoid waste or not ordering enough. The SI unit for volume is the cubic metre (m3). For example, how much concrete would you need for a sidewalk 1 m wide, 6 m long, and 10 cm thick?
Lesson Questions
In this lesson you will explore these questions.
-
How are volume and capacity measured in SI?
-
What are the common units for measuring volume in SI?
-
How are volumes and capacities described using one unit converted to another unit?
Assessment
You will complete the Lesson 3 Assignment for assessment. Download the Lesson 3 Assignment Booklet and save it in your course folder now. You will receive instructions on how to complete the Assignment Booklet later in the lesson. You will also be prompted to start working on the Unit 1 Project.
Remember to save all activities, including those that are not part of the Assignment, in your course folder.
Required Materials and Equipment
To complete this lesson, you will need 24 little cubes. You can use sugar cubes, children’s blocks, or cubes cut out of Styrofoam or other material.
1.12. Page 2
Module 1: The International System of Units (SI)
Get Started
prism: in geometry, a 3-D object that has two congruent and parallel faces (the top and bottom bases) and lateral faces that are parallelograms
Such a 3-D object is also known as a rectangular box. The following is a 3-D object known in geometry as a prism.
Suppose you wanted to determine the dimensions of a (rectangular) prism-shaped container that would hold exactly 24 sugar cubes with no wasted space. The cubes would have to be packed one against the other and tightly against the walls of the container. What would the dimensions of the box depend upon?
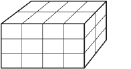
The diagram illustrates one possible prism-shaped arrangement. How many sugar cubes are there in the bottom layer?
How do you know there are 24 cubes altogether?
Think of a box made of thin cardboard, just large enough to hold this arrangement of cubes. You can then describe the dimensions of this box—4 cubes long, 2 cubes wide, and 3 cubes high. What would you get if you multiplied 4, 2, and 3 together?
volume: a measurement of how many cubic units into which an object or space may be divided
For example, if your living room is 5 m long by 3 m wide by 3 m high, its volume is
5 m × 3 m × 3 m = 45 m3.
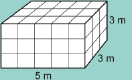
So, the volume of the box = length × width × height.
1.13. Page 3
Module 1: The International System of Units (SI)
Explore
By making various rectangular prisms from a set number of cubes, you can discover that volume can come in many shapes.
 Try This
Try This
For this activity, you will need 24 sugar cubes. You may instead use children’s blocks, or you could cut cubes out of Styrofoam, a block or cheese, or a potato. Use your ingenuity!
Arrange the 24 cubes to make as many (rectangular) prisms as you can. Use “Prism Data Table” to record your observations before responding to the questions below.
Visual Representation of Prism |
Prism Dimensions |
Product of Dimensions |
Volume |
|
2 wide, 3 high, 4 long |
2 × 3 × 4 = 24 |
24 cubes |
TT 1. Record the dimensions of each box that would contain your arrangements.
TT 2. Determine the product of the three dimensions together for each arrangement.
TT 3. Are all the arrangements different?
TT 4. What can you say about the volume of sugar each box holds?
TT 5. How can you determine how much each box can hold from its dimensions?
TT 6. Which is the “smallest” box that can hold the cubes? How did you judge the smallness of the box?
 Share
Share
It’s time to share your answers to TT 1 to TT 6. Remember that sharing work is an important part of learning. Use the following tips to ensure you get all the benefits from this sharing opportunity:
-
You have completed TT 1 to TT 6 to the best of your ability. The answers are in a form that you can share them easily with another student or with your teacher, if so directed.
-
Use your class discussion area, or another method indicated by your teacher, to post your answers to TT 1 to TT 6 and to view the work of the people you are sharing with.
-
Compare the answers for TT 1 to TT 6. You may want to share photos of the different sugar-cube arrangements you made. For TT 1 make sure you have included all the possible arrangements by looking at what other students have made. For TT 3, you may want to have some consensus on when an arrangement is to be considered different and when they are essentially the same. For TT 6, you may need some group thoughts and discussion on deciding on what smallness means. Discuss all differences between your answers until you have an agreement. If necessary, you may wish to involve your teacher in your discussion.
-
Revise your answers to TT 1 to TT 6 where necessary.
Save the revised copy of your work in your course folder. Ask your teacher whether you are to save a transcript of your discussion in your course folder as well.
1.14. Page 4
Module 1: The International System of Units (SI)
Bringing Ideas Together
In the Explore section, the volume of sugar each container held was given by the number of cubes of sugar. This is how all volumes are expressed—as the number of cubic units of space something occupies.
Remember, the volume of a rectangular box is found using the following formula:
volume = length × width × height
V = l × w × h
One commonly used unit of volume in SI is the cubic metre (m3).
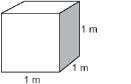
Now you will look at putting these linear units to work finding volumes.
Example 1
What is the volume in m3 of a rectangular box 60 cm long, 50 cm wide, and 40 cm high?
Solution
Because the volume is asked for in m3, convert the dimensions of the box to metres.
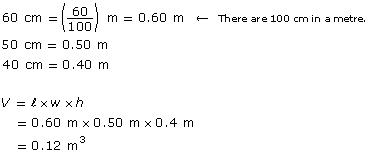
Small Units of Volume
Another common unit of volume is the cubic centimetre (cm3). The cubic centimetre is used for smaller objects, such as the volume of a milk container or the volume of a jewel.
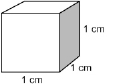
Did You Know?
Did you know the cubic centimetre is often referred to as the millilitre?
The cubic centimetre is much smaller than a cubic metre. How many cubic centimetres are there in a cubic metre?
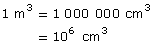
The interactive “SI Volume Conversion” can be used to show the conversion between units.
For example, by positioning the left slider next to m3 and the right slider to cm3 you can see that 1 m3 = 1 000 000 cm3 without doing any calculation. You can also use “SI Volume Conversion” to confirm the solutions in the examples, in the Self-Check questions that follow, and anywhere else you need to make volume conversions.
Example 2
Convert 0.12 m3 to cubic centimetres.
Solution
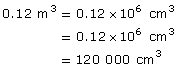
Recall from the previous example that 0.12 m3 was the volume of the rectangular box that measured 60 cm × 50 cm × 40 cm. You could have found the volume in cubic centimetres directly.
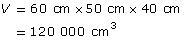
Either calculation gives the same value.
 Self-Check
Self-Check
Do the following questions. When you are finished, check your answers.
SC 1. Measure the dimensions of your bedroom closet.
- What is its volume in cubic centimetres?
- What is its volume in cubic metres?
- Which unit of volume is more appropriate? Why?
SC 2. Measure the dimensions of a cereal box.
- What is its volume in cubic centimetres?
- What is its volume in cubic metres?
- Which unit of volume is more appropriate? Why?
SC 3. Convert 0.05 m3 to cubic centimetres.
SC 4. How much concrete, measured in cubic metres, is required for a driveway 3 m wide, 20 m long, and 15 cm thick?
Capacity
People use the word capacity in various ways. For example, the capacity of an elevator can refer to the number of passengers the elevator can safely hold. In SI, capacity refers to the amount of liquid a container can hold, or the amount of space inside the container.
“Capacity Animation” shows different ways of understanding the word. You will see that capacity is used in a special way when using SI for measurement.
capacity: a measurement of how much a container can hold
Commonly, capacity refers to the amount of liquid that can be poured into a container, but it can also be used to refer to an amount of solid that can be placed into a container.
In the Explore section, you placed sugar cubes in various rectangular, prism-shaped arrangements. You considered the dimensions of the boxes—imagined to be made of thin cardboard—that would hold the sugar cubes. You found that the dimensions of the boxes allowed you to calculate the volume of sugar the boxes could hold. That is, the product of the dimensions gave you the capacity of the boxes.
 Try This
Try This
Look at various containers, such as soft-drink bottles, juice containers, and tinned goods. Record the metric measure of at least three containers. What SI unit is used?
litre: the capacity of a container having a volume of 1000 cm3
Since 1 L = 1000 mL, 1 mL = 1 cm3.

What does each of those SI symbols stand for?
What is the relationship between these units?
If you have a rectangular 1-L milk or juice container in the fridge, carefully measure its dimensions and calculate its volume. Round your answer to the nearest 1 cm3.
What is the relationship between the volume of the container and its 1-L capacity?
A container that has the shape of a cube measuring 10 cm (or 1 dm) on a side has a capacity of 1000 mL, or 1 L.

Here’s why.
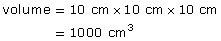
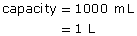
Why do you think a 1-L milk carton is not the shape of a cube having a side length of 10 cm?
Now you will practise applying these capacity units.
Example 3
On an Edmonton utility bill, the water a homeowner uses each month is reported in cubic metres.
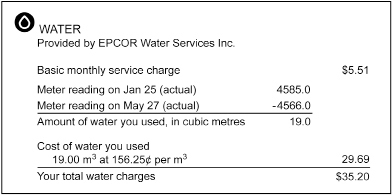
Reproduced courtesy of EPCOR
This homeowner used 19 m3 of water last month. If this water was for a family of four, how many litres were consumed per person?
Solution
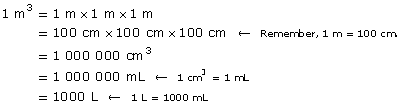
So, 19 m3 = 19 000 L.
Therefore, the consumption per person was
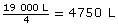
Example 4
Alexa has a small rectangular cooler she takes with her on picnics. The interior of the cooler is 32 cm long, 25 cm wide, and 25 cm deep. What is the capacity of the cooler in litres?
Solution
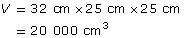
![]()
The cooler holds 20 L.
Units of Capacity
The prefixes of SI are used to form various units of capacity. You saw these prefixes when you investigated units of length, area, mass, and volume.
|
Prefix |
Symbol |
Factor |
|
mega |
M |
1 000 000 or 106 |
|
kilo |
k |
1000 or 103 |
|
hecto |
h |
100 or 102 |
|
deca |
da |
10 or 101 |
|
— |
— |
1 or 100 |
|
deci |
d |
0.1 or 10–1 |
|
centi |
c |
0.01 or 10–2 |
|
milli |
m |
0.001 or 10–3 |
|
micro |
µ |
0.000 001 or 10–6 |
The following tables show how the units of capacity and volume compare. See how the relationship 1 cm3 = 1 mL in one row connect the two tables so that the amounts on corresponding rows are equivalent.
Capacity |
Volume |
|||
Unit |
Symbol |
Symbol |
Unit |
|
|
1 millilitre |
1 mL |
|
1 cm3 |
1 cubic centimetre |
|
1000 litres or |
1000 L or 1 kL |
|
1 m3 |
1 cubic metre |
|
1 litre |
1 L |
|
1000 cm3 or 1 dm3 |
1000 cubic centimetres or 1 cubic decimetre |
Move the sliders in “Capacity Conversions” to convert 1 kL into litres.
This will allow you to confirm the relationship between kilolitre and litre indicated in the capacity-volume table.
 Self-Check
Self-Check
Now try these practice questions. To do these questions you will need to remember the relationships between volume and capacity. “Capacity Conversions” can be used to confirm your answers.
SC 5. A container of liquid laundry detergent holds 3.75 L. How many millilitres does this container hold?
SC 6. A soft-drink bottle holds 355 mL. How many litres does the container hold?
SC 7. Last month, the Ahenekiw family used 25 400 L of water in their home. How many cubic metres did they use?
SC 8. A rectangular aquarium is 50 cm long, 40 cm wide, and 30 cm deep. If it were filled with water, how many litres of water would the aquarium contain?
SC 9. When full, a rain barrel holds 220 L. What is the volume (in cubic metres) of the inside of the barrel?
SC 10. When full, a watering can holds 8 L. What is the volume of water it holds in cubic centimetres?

© Hannamariah/shutterstock
 Mastering Concepts
Mastering Concepts
Try these questions. When you are finished, check your answers.
The area of Vancouver is almost 115 km2. On average, the city receives 1200 mm of precipitation each year.
MC 1. How many litres of water does this precipitation represent?
MC 2. There are seven billion people on Earth. If the water Vancouver receives as precipitation were divided equally, how many litres would each person receive. Round your answer to the nearest litre.
1.15. Page 5
Module 1: The International System of Units (SI)
Lesson Summary

© Christina Richards/shutterstock
Ordering concrete for a project involves careful planning, measurement, and calculations. The amount ordered may involve adding a small percentage extra. In order to keep costs down and to ensure the job can be completed with the amount of concrete delivered, mathematics, similar to what you explored in this lesson, are a critical component.
In this lesson, you explored these questions:
-
How are volume and capacity measured in SI?
-
What are the common units for measuring volume in SI?
-
How are volumes and capacities described using one unit converted to another unit?
To answer these questions, you examined the relationships among the cubic metre, cubic centimetre, millilitre, and litre. As in the previous two lessons, you discovered these relationships are based on powers of 10; and, to convert among these units you just had to move the decimal to the left or right.
 Assignment
Assignment
Retrieve the Lesson 3 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment Booklet. Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Unit Project
Before you move on to the next lesson, you should progress in completing the SI section of your Unit 1 Project. In your scale drawing, identify a volume that would be appropriate for conversion between measuring systems. For more information about this and later steps in the Unit 1 Project, refer to the Unit 1 Project.
1.16. Lesson 4
Module 1: The International System of Units (SI)
Lesson 4: Mass
Focus

© Stephen Coburn/shutterstock
Will the product that you develop for your Unit 1 Project be shipped to market?
Most produce in grocery stores is sold by weight. Recently, in a flyer from a local supermarket, apples and peaches were advertised at $2.16/kg, cantaloupe at $1.50/kg, and mushrooms at $5.47/kg. These prices are quoted in terms of kilograms—an SI (metric) measure of mass. Scales to weigh produce are available in most stores for customers to use. Have you used a scale similar to the one in the photograph to weigh produce before making your purchases?
Lesson Questions
In this lesson you will explore these questions:
- How is mass measured in SI?
- What are the common units for measuring mass in SI?
- How is one unit used to describe a mass converted to another unit?
Assessment
You will complete the Lesson 4 Assignment Booklet for assessment. Download the Lesson 4 Assignment Booklet and save it in your course folder now. You will receive instructions on how to complete the Assignment Booklet later in the lesson. You will also be prompted to start working on the Unit 1 Project.
Remember to save all activities, including those that are not part of the Assignment, in your course folder.
Required Materials and Equipment
In this lesson you will need your calculator and access to the Internet.
1.17. Page 2
Module 1: The International System of Units (SI)
Get Started
Do you have an operator’s licence or a passport? If you do, take a closer look at either of these pieces of identification now.

© Alberta’s Operator’s Licence (2009 Design),<http://www.servicealberta.gov.ab.ca/
images/DriversLicence/proofing-new-v1.jpg> (Edmonton: Service Alberta, 2009).
(23 November 2009). Reproduced by permission.
Notice that your physical characteristics include SI (metric) measures for your height and weight. In the sample Alberta licence, what is Erin’s weight?
weight: a measure of the force of gravity on an object
mass: a measure of the quantity of matter in an object
In everyday conversation, people use the terms weight and mass interchangeably. The terms are related, but strictly speaking, weight and mass have different meanings. Your weight depends on gravity. For example, on the moon, where the force of gravity is less than on Earth, your weight would be less, but you would still be you—mass-wise.

© Stavchansky Yakov/shutterstock
The kilogram is a unit of mass, but it is commonly used to indicate weight. What is your weight (mass) in kilograms? If you have access to a bathroom scale, weigh yourself now. If you’ve been to a doctor’s office or health clinic, the scales there use a balance beam and are more accurate.
1.18. Page 3
Module 1: The International System of Units (SI)
Explore
A person’s mass may be found on a driver’s licence and on medical records. Many sports teams show the mass of players on the team roster. The next activity allows you to investigate the significance of the mass of a professional athlete.
 Try This
Try This
What is your favourite professional sports team? Perhaps you have a favourite hockey, football, or basketball team. Choose this team for this next activity. In this activity you will investigate the mass of players and the effect of a player’s mass on performance.
You will need your calculator and access to the Internet.
Step 1: Access your chosen team’s roster on the Internet. Examine the player statistics.
Step 2: Prepare a three-column chart that lists the players’ statistics. You should have columns for each player’s name, position, and mass.
The players’ weight may be given in pounds. If the player’s weight is given in pounds, divide the weight in pounds by 2.2 to find the SI (metric) equivalent. For example, Jordin Tootoo plays for the Nashville Predators in the National Hockey League. His weight is listed at 194 pounds. What is his weight in kilograms?
TT 1. What is the weight, in kilograms, of the heaviest player on the team you chose?
TT 2. What is the weight, in kilograms, of the lightest player on your favourite team?
TT 3. What is the difference between the weights of the heaviest and lightest player on the team?
TT 4. From the data you have collected, and from your own personal experience, do you feel the mass of the individual affects his or her ability to excel in a certain position or sport? Or do you think the position or sport influences the mass of the athlete instead? Explain.
 Share
Share
It’s time to share your answers to TT 1 to TT 4. Remember that sharing work is an important part of learning. Use the following tips to ensure you get all the benefits from this sharing opportunity:
- You have completed TT 1 to TT 4 to the best of your ability. The answers are in a form that you can share them easily with another student or with your teacher, if so directed.
- Use the discussion area for your class, or another method indicated by your teacher, to post your answers to TT 1 to TT 4 and to view the work of the people you are sharing with.
- Compare answers for TT 1 to TT 4. Identify where you have similar answers and where your answers are different. Discuss all differences between the answers until you have an agreement. If necessary, you may wish to involve your teacher in your discussion. For TT 4, you may want to come to some agreement through discussion on how the mass of a player and the player’s performance are related. To convince others, you may use examples to support your opinion.
- Revise your answers to TT 1 to TT 4 where necessary.
Save the revised copy of your work in your course folder. Consult your teacher on whether you are to save a transcript of your discussion in your course folder as well.
1.19. Page 4
Module 1: The International System of Units (SI)
Bringing Ideas Together
A kilogram is equal to the mass of a certain cylinder of platinum-iridium alloy kept at the International Bureau of Weights and Measures in France.
The base unit of mass in SI (metric) is the kilogram (kg). Originally, in 1796 in France, during the French Revolution, the kilogram was defined as the mass of 1 L of ice water. A few years later, it was redefined as the mass of 1 L of water at 4°C, the temperature when water is its most dense. However, for uniformity, metal cylinders were manufactured that came as close as possible to this mass.

Copyright © BIPM. Reproduced with permission.
The metal cylinder used today was manufactured in the 1890s. It is made from a metal alloy of platinum and iridium because of the alloy’s stability. This cylinder is called the International Kilogram Prototype and is kept in a vault at the Internal Bureau of Weights and Measures (BIPM) in Sèvres, France, near Paris. This is the standard used by science, industry, and commerce around the world.
Scientists are in the process of trying to agree on a different way of defining the kilogram to make it easier to duplicate. Agreement may be reached in 2011.
In the problems in this lesson, the mass of 1 L of water provides a very good approximation of the kilogram. If you have access to a litre of milk, or perhaps a litre of bottled water or pop, go and take it out of the fridge now. When you lifted the container, you lifted a 1-kg mass. What other everyday objects can you name that have about a 1-kg mass?
Example 1
Marty weighed himself on a bathroom scale. He weighed 61 kg. Later that day, at the store where he works, he lifted five dozen bottles of water into the trunk of a customer’s car. He told the customer he just lifted his own weight in water. Was Marty correct in what he said?
Solution
Five dozen bottles is 5 × 12, or 60 bottles. Each bottle contains 1 L, and 60 L of water has a mass of 60 kg, which is close to Marty’s weight. Including the containers, the total would be at least 61 kg. Marty was telling the truth!
Comparing Units
So, how do different units of mass relate to one another?
There are two common units derived from the kilogram. What does the prefix kilo mean in kilogram? How many grams are there in a kilogram?
Remember that 1 L of water has a mass of 1 kg. But 1 L = 1000 mL and 1 kg = 1000 g. So, 1 mL of water has a mass of 1 g.
Do you remember what the volume of 1 mL of water is?
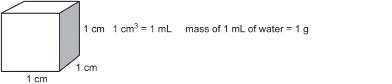
A small grape or raisin has a mass of about 11 grams. Can you think of other objects that are 1 g in mass?
Example 2
A Canadian dime has a mass of 1.75 grams.
- Express the mass of the dime in kilograms.
- About how many dimes are there in 1 kg?
Solution

- 1 kg = 1000 g
1 dime = 1.75 g
So, the number of dimes in 1000 g is
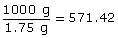
There are about 571 dimes in a kilogram, or a total of $57.10 in dimes.
 Try This
Try This
The previous examples showed that converting among SI units of mass involves only powers of 10. So, mass unit conversion only involves the movement of the decimal. See this happen in “Mass Conversions.” Go back to Example 2 and use “Mass Conversions” to confirm the conversion from grams to kilograms.
Large Masses
That is, 1 t = 103 kg.
Another unit derived from the kilogram is the tonne (t). The tonne is used for measuring large masses, such as the mass of concrete in a bridge, the mass of goods in a truck and trailer unit, or the mass of an airplane.
In the lesson on volume, you explored the number of litres in 1 m3. Do you remember that 1 m3 = 1000 L? So, what would the mass be of 1 m3 of water?
Example 3
A Canadair 415 water bomber used in fighting forest fires can hold 6137 L of water. What is the mass, in tonnes, of water it can release?
Solution
The mass of 6137 L of water is 6137 kg.
![]()
The water bomber holds 6.137 t of water in its tanks.
Example 4

© joyfull/shutterstock
An Antonov 225, the world’s largest cargo plane, can carry 250 t. What is its cargo capacity in kilograms?
Solution
![]()
The Antonov can haul 250 000 kg.
 Self-Check
Self-Check
Do the following questions. Where conversion between kilograms and grams are involved, you may use “Mass Conversions” to help you.
SC 1. Every day, Maria drinks at least 1.75 L of water. What mass of water would she drink in 2013 measured in
- kilograms
- grams
SC 2. The blue whale can grow to over 170 000 kg. What is that mass in tonnes?
SC 3. The Darias’ baby was 3125 g at birth. How much did the baby weigh in kilograms?
SC 4. The Canadian $1 coin is 7 g in mass. In 2007, the Royal Canadian Mint struck 36 424 000 of these coins. What is the total mass of all of these coins in tonnes?
SC 5. A package of 50 cheese slices weighs 0.5 kg. What is the mass, in grams, of each slice?
SC 6. During the winter, there are over 1400 km of ice roads and ice crossings in the Northwest Territories. The total weight of a truck and cargo travelling to Inuvik could weigh over 45 t. What is 45 t in kilograms?
SC 7. A package of meat is labelled 1.37 kg. What is its weight in grams?
SC 8. Convert 67 000 g to tonnes.
SC 9. A 2-kg sausage is divided into 100-g portions. How many portions are there?
SC 10. Cream puffs are advertised by a local store for $3.49 for a 250-g package. What is the price per kilogram?
 Mastering Concepts
Mastering Concepts
If you have mastered the concepts of this lesson and would like a challenge, try these questions. You might use “Mass Conversions” to help you make the conversion between mass units. When you are finished, check your answers.
The quantity of active ingredients in a pill or vitamin tablet is often quoted in milligrams (mg).
MC 1. What does the prefix m in mg mean?
MC 2. How many milligrams are there in 1 g?
MC 3. A baby Aspirin contains 75 mg of medication. Convert 75 mg to grams.
1.20. Page 5
Module 1: The International System of Units (SI)
Lesson Summary

© ownway/shutterstock
Do you check your bill when you purchase groceries from a supermarket? Prices of items that are sold by weight, such as meats and vegetables, are listed per kilogram. As a careful shopper, you should be familiar with the SI units for mass.
In this lesson you explored these questions.
- How is mass measured in SI?
- What are the common units for measuring mass in SI?
- How is one unit used to describe a mass converted to another unit?
Check your level of understanding of the materials covered in this lesson by completing “Lesson 4 Traffic Lights.” If you select an amber or red traffic light in the multimedia piece, you will receive information about additional work you can complete to improve your understanding of the topics. Complete the suggested work before you proceed to the Lesson 4 Assignment. If you experience difficulty, contact your teacher before starting the Lesson 4 Assignment.
You discovered that the base unit for mass in SI is the kilogram, from which gram and tonne are derived. You examined the relationships among the gram, kilogram, and tonne. You discovered that to convert among these units, you just have to move the decimal to the left or right.
 Assignment
Assignment
Retrieve the Lesson 4 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment Booklet. Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Unit Project
Before you move on to the next lesson, you should be close to completing the SI (metric) section of the Unit 1 Project.
1.21. Lesson 5
Module 1: The International System of Units (SI)
Lesson 5: Temperature
Focus

© Galyna Andrushko/shutterstock
If you are developing a habitat for your Unit 1 Project, the type of habitat you design will have to take into account the extremes of weather.
For those who enjoy outdoor activities, winter time, whether it’s sunny or cloudy, simply means dressing for the weather and enjoying the ice, snow, and scenery. Skiing, skating, curling, snowmobiling, and ice fishing are a few winter sports enjoyed by Canadians across the country. Of course, occasionally the temperature is too cold to go outdoors safely for extended periods of time. What do you think the temperature was on the day the photograph was taken?
Lesson Questions
In this lesson you will explore these questions:
-
How is temperature measured in SI?
-
What is the history of the SI temperature scale?
-
How is the SI temperature scale used today?
Assessment
You will complete the Lesson 5 Assignment Booklet for assessment. Download the Lesson 5 Assignment Booklet and save it in your course folder now. You will receive instructions on how to complete the Assignment Booklet later in the lesson. You will also be prompted to start working on the Unit 1 Project.
Remember to save all activities, including those that are not part of the Assignment, in your course folder.
Required Materials and Equipment
To complete this lesson you will need a thermometer and access to the Internet.
1.22. Page 2
Module 1: The International System of Units (SI)
Get Started
How well can you estimate temperature from how warm or cold an object or environment feels? Try the following test to see how reliable estimating the temperature this way is.
 Try This
Try This
In this activity you will put to the test your sense of how warm or cold something feels.

Prepare three bowls of water as shown. You will fill one bowl with room-temperature water. Then fill another bowl with hot water, and fill the remaining bowl with ice-cold water. Be careful! The hot water should be as hot as you can bear without scalding yourself. The bowl with ice-cold water could contain ice cubes to maintain its temperature.
Next, put your left hand in the hot water and your right hand in the ice water. Keep your hands immersed for a count of 30. Then, put both hands in the bowl filled with room-temperature water. What did you notice after you placed your hands in the room-temperature water?
Gauging Temperature
The human body is not a good gauge of temperature. If you’ve been outside on a cold day and then come indoors, the indoor temperature will feel hot. But, someone coming out of a hot bath into the same room will feel cold.
For accurate temperatures, you need a thermometer.
1.23. Page 3
Module 1: The International System of Units (SI)
Explore
Although the human body is not a good gauge of temperature, the human body is sensitive to outdoor temperatures. Outdoor temperatures affect the type of clothing people need to wear to avoid discomfort or even injury from exposure to temperature extremes. By investigating temperatures in various places in Canada, and thinking about what you would need to dress in these places, you will become more familiar with the Celsius scale of temperatures.
 Try This
Try This
In this activity you will explore temperatures in Celsius from around the country. Think about how you would need to dress for the weather in each locale.
To complete this activity, you will need access to the Internet. The Environment Canada website should have all the information you need. A simple Internet search will take you to that website or to another appropriate weather site.
TT 1. Complete a table like the following. Using degrees Celsius, record yesterday’s highest and lowest temperatures for each community listed in the table.
TEMPERATURES IN DEGREES CELSIUS
|
Community |
Highest (Maximum) |
Lowest (Minimum) |
|
Edmonton, AB |
||
|
Iqaluit, NU |
||
|
Regina, SK |
||
|
Vancouver, BC |
||
|
Whitehorse, YK |
||
|
Winnipeg, MB |
||
|
Yellowknife, NT |
TT 2. Which community had the highest temperature? Describe how you would feel at that temperature.
TT 3. Which community had the lowest temperature? Describe how you would feel at that temperature.
Save the revised copy of your work in your course folder.
1.24. Page 4
Module 1: The International System of Units (SI)
Bringing Ideas Together
Did You Know?
The Inuit have six words for snow. To travel in the Arctic, you need to know how various conditions can affect your travel by sled or by snowmobile.
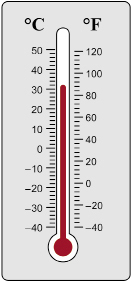
Celsius: a temperature scale commonly used in every major country throughout the world, except the United States
The thermometer in the diagram gives temperature in degrees Celsius and Fahrenheit. The Celsius scale gives temperature readings in SI. In Lesson 5 of Module 2, you will explore the Fahrenheit scale.

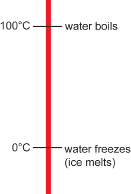
The Celsius temperature scale is named after the Swedish scientist Anders Celsius, who invented a similar temperature scale in the 1740s. Anders Celsius divided the temperature difference between the boiling point of water and the temperature at which ice melts into 100°.
The modern Celsius scale is very similar in design. The freezing point of water is almost exactly 0°C, and the boiling point of water is almost exactly 100°C, so the two temperatures, for all practical purposes, are 100° apart.
Explore the interactive piece “The Celsius Scale” to reacquaint yourself with important benchmarks on the Celsius scale. Watch the thermometer level and the descriptors for different temperatures.
 Try This
Try This
Using the interactive “Real-World Benchmarks on the Celsius Scale,” place some familiar events or experiences along the appropriate position on the Celsius thermometer. When the event is dragged close to the appropriate spot, the event will snap into place.
You may decide to place a screen shot of your completed thermometer in your course folder for reference.
Temperature Measurements
In Iqaluit, Nunavut, the average daily temperature during the month of February is −26°C. In order to determine this average, someone had to perform calculations based on temperature measurements.
The following examples show some more contexts for calculations involving temperature measurements.
Example 1
The coldest recorded temperature in Canada is −63°C. This temperature was recorded on February 3, 1947, at Snag, Yukon. The hottest recorded temperature was 45°C on July 5, 1947, at Midale and Yellowgrass, Saskatchewan. What is the difference between these two temperatures?
Solution
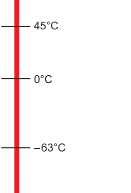
The high temperature is 45 degrees above freezing. The low temperature is 63 degrees below freezing. The difference between these two temperatures is
45 + 63 = 108°C.
Another way to find this difference is to subtract −63 from 45.
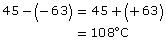
Either method gives you the same result. A temperature of 45°C is 108°C warmer than −63°C. An interesting fact is that this difference is greater than the difference between the freezing point of water (0°C) and the boiling point of water (100°C); that difference is only 100 degrees.
Example 2
One day last spring, Ester recorded the maximum (highest) daily temperature on her farm. The maximum temperature was +13°C. The minimum (lowest) temperature was −7°C. What was the average temperature that day?
Solution

The high of +13°C is 20°C warmer than −7°C. So, the average temperature is 10°C colder than +13°C and 10°C warmer than −7°C. So, the average temperature was
13 − 10 = +3°C or − 7 + 10 = +3°C
Can you suggest another way of finding the average?
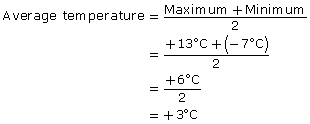
The average temperature on Ester’s farm was +3°C.
Temperature Differences
Use the interactive piece “Average Temperature and Temperature Difference” to confirm the temperature difference and average temperature calculated in the solutions of the previous examples. Just drag the sliders for the temperatures. You can also use the arrow keys to move the sliders.
 Self-Check
Self-Check
To complete this practice exercise, you will need access to the Internet. Do the following questions. When you are finished, check your answers.
SC 1. On September 5, 2009, at Beaverlodge, Alberta, the maximum temperature was 19.1°C and the minimum temperature was 3.7°C.
- Describe how you would dress for comfort at each temperature.
- What was the average temperature?
SC 2. What temperature should your refrigerator be set at to keep food from spoiling? Research your answer using the Internet.
SC 3. To what temperature should the interior of a hamburger be cooked before it is safe to eat? Research your answer using the Internet.
SC 4. What are the most common oven temperatures in degrees Celsius for baking? Research your answer using the Internet.
SC 5. When you are outdoors in winter, you will feel much colder in a strong wind than when the wind is calm. Environment Canada provides a chart for calculating wind chill on its website.
WIND CHILL FOR TEMPERATURES FROM +5 TO −20°C
V10 (km/h) |
Tair (°C) |
|||||
5 |
0 |
−5 |
−10 |
−15 |
−20 |
|
5 |
4 |
−2 |
−7 |
−13 |
−19 |
−24 |
10 |
3 |
−3 |
−9 |
−15 |
−21 |
−27 |
15 |
2 |
−4 |
−11 |
−17 |
−23 |
−29 |
20 |
1 |
−5 |
−12 |
−18 |
−24 |
−30 |
25 |
1 |
−6 |
−12 |
−19 |
−25 |
−32 |
30 |
0 |
−6 |
−13 |
−20 |
−26 |
−33 |
35 |
0 |
−7 |
−14 |
−20 |
−27 |
−33 |
40 |
−1 |
−7 |
−14 |
−21 |
−27 |
−34 |
45 |
−1 |
−-8 |
−15 |
−21 |
−28 |
−35 |
50 |
−1 |
−8 |
−15 |
−22 |
−29 |
−35 |
55 |
−2 |
−8 |
−15 |
−22 |
−29 |
−36 |
60 |
−2 |
−9 |
−16 |
−23 |
−30 |
−36 |
65 |
−2 |
−9 |
−16 |
−23 |
−30 |
−37 |
70 |
−2 |
−9 |
−16 |
−23 |
−30 |
−37 |
75 |
−3 |
−10 |
−17 |
−24 |
−31 |
−38 |
80 |
−3 |
−10 |
−17 |
−24 |
−31 |
−38 |
Credit: Wind Chill Calculation Chart. http://www.msc.ec.gc.ca/education/windchill/windchill_chart_e.cfm. Environment Canada, 2004. Reproduced with the permission of the Minister of Public Works and
Government Services Canada, 2009.
- What does the temperature feel like when the wind is 30 km/h and the outdoor temperature is +0°C?
- What does the temperature feel like when the wind is 40 km/h wind and the outdoor temperature is −15°C?
 Mastering Concepts
Mastering Concepts
Scientists often use the Kelvin (K) temperature scale. Zero (0 K) is absolute zero—the coldest possible temperature. It is also the temperature at which all molecular motion is at a minimum. The temperature 0 K is approximately −273°C.
Because degrees are the same size on both scales, the freezing point of water, or 0°C, must be 273 K. The formula for converting degrees Celsius to degrees Kelvin is K = °C +273.
For example, room temperature, or 20°C, would be
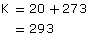
MC 1. Convert each of the following temperatures to degrees Kelvin:
- body temperature, 37°C
- the boiling point of water, 100°C
- a moderate oven temperature, 175°C
1.25. Page 5
Module 1: The International System of Units (SI)
Lesson Summary

© Hannamariah/shutterstock
A knowledge of temperature is important for more than just helping you dress appropriately for the weather. For example, meats must be cooked to high-enough temperatures to avoid illness. For instance, the Canadian Food Inspection Agency recommends that whole poultry, such as turkey, duck, or goose, should be cooked to an internal temperature of 85°C. You can check the internal temperature using a meat thermometer.
In this lesson you explored these questions:
-
How is temperature measured in SI?
-
What is the history of the SI temperature scale?
-
How is the SI temperature scale used today?
Check your level of understanding of the materials covered in this lesson by completing “Lesson 5 Traffic Lights.” If you select an amber or red traffic light in the multimedia piece, you will receive information about additional work you can complete to improve your understanding of the topics. Complete the suggested work before you proceed to the Lesson 5 Assignment. If you experience difficulty, contact your teacher before starting the Lesson 5 Assignment.
In answering these questions, you discovered that the Celsius temperature scale is part of the SI. You explored how the benchmarks on the Celsius scales are related to the melting point of ice and the boiling point of water.
 Assignment
Assignment
Retrieve the Lesson 5 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment Booklet. Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Unit Project
Before you move on to the next part of this unit, you should complete the SI portion of your Unit 1 Project. Please note that when you complete your work later in this unit, you will be asked to indicate measurements using both SI and imperial units. Also identify a calculated area in the work you’ve done so far that you will convert to imperial measure in Module 2. For more information about this step and later steps, refer to the Unit 1 Project.
1.26. Module 1 Summary
Module 1: The International System of Units (SI)
Module 1 Summary
Copyright © BIPM. Reproduced with permission.
The graphic you see represents the global agreement on weights and measures. The International Bureau of Weights and Measures, near Paris, France, oversees discussions regarding the SI units used around the world. In the graphic shown, you will recognize the symbols for metre (m), kilogram (kg), and second (s). These symbols are an important part of the International System of Units (SI).
In this module you used these SI symbols as you explored the following question:
What is the International System of Units (SI), and how is it used to measure length, area, volume, mass, and temperature?
The lessons in this module allowed you to develop an answer to this question. As you completed the activities in this module, you learned how the SI is used in various occupations. You personally used the SI in designing your Unit 1 Project.
A picture can tell a story. The Module 1 Lessons Summary is a collection of images from each lesson that describes the math you explored. What do you remember about each image? Can you relate each image to something new you learned in this module? Watch “Module 1 Lessons Summary” now.