Module 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Biology 30 [5 cr] - AB Ed copy 1 |
| Book: | Module 2 |
| Printed by: | Guest user |
| Date: | Thursday, 18 September 2025, 7:17 PM |
Description
Created by IMSreader
Table of contents
- 1. Module 2
- 1.1. Lesson 1
- 1.2. Page 2
- 1.3. Page 3
- 1.4. Page 4
- 1.5. Page 5
- 1.6. Lesson 2
- 1.7. Page 2
- 1.8. Page 3
- 1.9. Page 4
- 1.10. Page 5
- 1.11. Lesson 3
- 1.12. Page 2
- 1.13. Page 3
- 1.14. Page 4
- 1.15. Page 5
- 1.16. Lesson 4
- 1.17. Page 2
- 1.18. Page 3
- 1.19. Page 4
- 1.20. Page 5
- 1.21. Lesson 5
- 1.22. Page 2
- 1.23. Page 3
- 1.24. Page 4
- 1.25. Page 5
- 1.26. Module 2 Summary
1. Module 2
Module 2: The Imperial System
Module 2 Introduction

© Maisei Raman/shutterstock
Canada is a trading nation with strong links to the country’s past. Canada is a member of the British Commonwealth. Until the latter half of the twentieth century, Canada used the system of weights and measures that evolved in Britain. This system is known as the imperial system.
You likely recognize many units from the imperial system, such as the foot, yard, and mile, the acre, the gallon, the pound, and degrees Fahrenheit. Canada’s largest trading partner, the United States, still uses a modified form of the imperial system. United States’ customary units and imperial units are still used in Canada in many of the trades. Carpenters, plumbers, and mechanics, to name a few, must be familiar with metric and imperial units.
Once you have completed this module, you should have the necessary skills to complete the second half of your Unit 1 Project.
In this module you will explore the following questions:
- What is the imperial system of weights and measures and how is it used to measure length, area, volume, capacity, weight, and temperature?
- What are the relationships among metric units, imperial units, and American customary units?
Save a copy of the Module 2 Glossary in your course folder now. The Module 2 Glossary is a list of all of the new terms you will see in the lessons. Each time you see a definition, open your copy of the Glossary. Use the space available to add notes or drawings to help your understanding. You will be able to use your personal Glossary as a study tool.
1.1. Lesson 1
Module 2: The Imperial System
Lesson 1: Length
Focus
Did You Know?
The imperial system of weights and measures was first defined in 1824—less than 200 years ago!

© Paul Matthew Photography/shutterstock
Have you thought about a career in the construction trades? In Canada, many of the trades still work with feet (ft or ′) and inches (in or ″)—part of the imperial system of weights and measures. If you talk to framing carpenters, they will point out that interior drywall and exterior sheeting commonly used throughout North America is manufactured in 4-by-8-ft lengths.
Drywall and sheeting are screwed to vertical posts called studs. Framing carpenters must carefully measure the horizontal distances between studs so the ends of the sheeting or drywall fall in the middle of the studs and can be screwed on securely. Do you know how far apart vertical studs are in a new home?
In this lesson you will explore the following questions:
- How are lengths and distances commonly measured in the imperial system?
- What is the history of length and distance units in the imperial system?
- How are imperial system units related?
- How are imperial system units applied in practical situations?
- How can units of length and distance be converted between the imperial and metric systems?
Assessment
You will complete the Lesson 1 Assignment Booklet for assessment. Download the Lesson 1 Assignment Booklet and save it in your course folder now. You will receive instructions on how to complete the Assignment Booklet later in the lesson. You will also be prompted to work on the Unit 1 Project.
There are other activities that you will complete throughout this lesson. It is important to complete all activities and save them in your course folder. Your teacher may ask to see your work at any time.
The lesson provides you with opportunities to investigate, review examples, and practise the knowledge and skills you are learning. In Self-Check activities you can compare your answers to see if you are on track. If you are having difficulty with concepts or calculations, contact your teacher.
Required Materials and Equipment
You will need a ruler or a tape measure that shows inches.
1.2. Page 2
Module 2: The Imperial System
Get Started
Did You Know?
Egyptians invented paper made from the fibres of the papyrus plant more than 5000 years ago.
In ancient times, people used parts of their bodies as units of measure. You may have heard of the cubit. In Ancient Egypt, the cubit was the length of your forearm—the distance from your elbow to the tip of your middle finger.
 Try This
Try This
If possible, work with a partner to complete this activity.
In this activity you will look at some of the origins of the imperial system. In each step there is a question or two you must answer.
Step 1: Working with a partner, measure how long, in metres, a cubit is for both you and your partner.
TT 1. Is your cubit the same as your partner’s cubit?
Step 2: Use your cubit to measure the width and height of a door.
TT 2. What are the door’s dimensions in cubits?
Step 3: Another common unit of measure was the length of a person’s foot and, for smaller measures, the width of a person’s thumb just below the nail. On a sheet of paper, carefully trace your foot. (Save your tracing. You will use your tracing again later in this lesson.)
TT 3. How many thumb-widths long is the tracing of your foot?
TT 4. What fraction of your traced foot is your thumb width?
 Share
Share
It’s time to share your answers to TT 1–TT 4. Remember that sharing work is an important part of learning. Use the following tips to ensure you get all the benefits from this sharing opportunity:
- Complete the questions to the best of your ability. Make sure your answers are in a form that you can easily share them with another student or with your teacher, if so directed.
- Use your class discussion area, or another method indicated by your teacher, to post your answers and to view the work of the people you are sharing with.
- Compare your answers to the other posted answers. Identify where you have similar answers and where your answers are different. Discuss all differences between answers until you agree on the answers. If necessary, you may wish to involve your teacher in your discussion.
- Revise your answers where necessary.
Save a revised copy of your work in your course folder. Ask your teacher whether you should also save a summary of your discussion in your course folder.
The imperial system does not use cubits, but the standard foot and the inch, which is about the width of a thumb, are among the imperial system’s common units of linear measure.
Do you agree that because the size of feet and thumbs differs from person to person, standard sizes must be set in order for measurements to be consistent?
Did you find that your foot was about 12 thumbs in width, and each thumb was 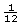 of a foot?
of a foot?
To work with lengths in the imperial system, you will need to polish your skills in adding and subtracting fractions. For instance, what is ![]() ?
?
Step 4: Look at the following example.
Example 1
Add the following fractions.
![]()
Solution

 Self-Check
Self-Check
SC 1.
Solve the following.
![]()
1.3. Page 3
Module 2: The Imperial System
Explore
In this lesson you will use a ruler or tape measure with inches marked. By studying the markings on a ruler, you can learn to use your ruler to measure lengths properly.
 Try This
Try This
Have a look at your ruler or tape measure. It should look similar to the one pictured.
Does your ruler or tape measure, in feet and inches, look similar to the ruler shown?

Look at the divisions on the ruler shown. The longest vertical lines on the ruler are located every whole inch. These lines are at 1 in, 2 in, 3 in, and so on.
TT 5. What do the slightly shorter lines mark (line A in the image)? What would the measures be at such a line between 2 in and 3 in?
TT 6. What fraction do the next shorter lines mark (line B in the image)? What measures do these vertical lines represent between the 1-in and 2-in marks?
TT 7. What do the next shorter lines represent (line C in the image)?
TT 8. So, what can you say about the shorter and shorter vertical lines?
TT 9. What is the smallest fraction of an inch that is shown between 0 in and 1 in?
TT 10. Use your ruler or tape measure to measure at least four items. Use the lines on your tape measure or ruler to be as precise as you can be.
 Share
Share
It’s time to share your answers to TT 5–TT 10. Remember that sharing work is an important part of learning. Use the following tips to ensure you get all the benefits from this sharing opportunity:
- Complete the questions to the best of your ability. Make sure your answers are in a form that you can easily share with another student or with your teacher, if so directed.
- Use your class discussion area, or another method indicated by your teacher, to post your answers and to view the work of the people you’re sharing with.
- Compare your answers to the other posted answers. Identify where you have similar answers and where your answers are different. Discuss all differences between answers until you agree on the answers. If necessary, you may wish to involve your teacher in your discussion.
- Revise your answers where necessary.
Save a revised copy of your work in your course folder. Ask your teacher whether you should also save a summary of your discussion in your course folder.
1.4. Page 4
Module 2: The Imperial System
Bringing Ideas Together
inch: a unit of length in the imperial system
A measure of 1 inch can be written as 1 in or 12.
In Get Started you discovered that there are about 12 thumb widths in a foot. The Romans also divided their foot measure into 12 parts. The word inch comes from the Latin word uncia, which means a 12th part. In some languages the same word is used for thumb and inch. For example, in French, the word for both thumb and inch is pouce.
The modern inch is exactly 2.54 cm in length. So, a length of 2 in is about two thumb widths, or 5 cm.
The Saxons were a people who settled in Britain after the Romans left. The Saxons used three grains of barley placed end-to-end to define their inch. Barley seeds are very uniform in size. The Saxon inch was very close to today’s inch, but it was longer than a Roman inch. So, as a unit of measure, the Saxon foot of 12 inches was longer than the Roman foot.
Do you remember tracing your own foot at the beginning of this lesson? Retrieve your tracing and measure it using your ruler or tape measure. Is your foot more or less than 12 of today’s inches?
foot: a unit of length in the imperial system equal to 12 in
A measure of one foot can be expressed as 1 ft or 1′.
Does your ruler or tape measure have centimetres marked? If so, check to see how many centimetres there are in one inch. Can you also see how many centimetres there are in one foot?
Since 1 in is equal to 2.54 cm, 1 ft is 12 × 2.54 cm, or 30.48 cm. Is that what you found when you looked at 1 ft on your ruler or tape measure?
Often measurements are quoted in feet and inches. Do you know your height in feet and inches?
Converting Feet and Inches
Example 2 shows how feet are converted to inches.
Example 2
An Iroquois longhouse was 79′11″ long. What was the length of the longhouse in inches?
Solution
1 ft = 12 in
So,
![]()
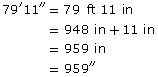
The Iroquois longhouse was 959 in long.
Example 3
Example 3 shows how inches are converted to feet and inches.
Meilin is 53 in tall. What is her height in feet and inches?
View the animated “Example 3 Solution.”
Note: In this example, a calculator was used to do the division. If long division were used, the quotient would be the number of feet, and the remainder would be the number of inches.
Adding Fractions of Inches
Example 4
John and his mother are finishing their basement. For the outside walls, they plan to use 2-by-4 framing lumber. Framing lumber sold as 2-by-4 pieces actually measure just ![]() . The lumber is to be covered with gypsum board measuring
. The lumber is to be covered with gypsum board measuring ![]() in. How thick will this added layer of the wall be?
in. How thick will this added layer of the wall be?
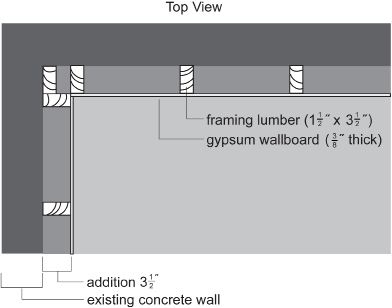
Solution

A 2-by-4 is actually ![]() . The total thickness of the framing lumber and wallboard is
. The total thickness of the framing lumber and wallboard is ![]() . These fractions can be added using a ruler. Look at the ruler shown.
. These fractions can be added using a ruler. Look at the ruler shown.
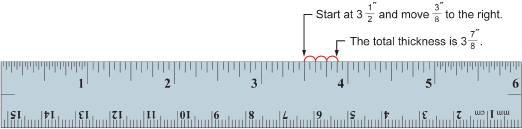
You can also add the fractions using pencil and paper.
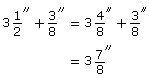
Try this using “Simulated Ruler.” Starting at ![]() , move
, move ![]() of an inch to the right. Once in this new position, the readout will show the sum.
of an inch to the right. Once in this new position, the readout will show the sum.
Subtracting Fractions of Inches
Example 5

© Grafos1fp/Dreamstime
Pat wants to plane some wood off the width of a 2-by-6. If a 2-by-6 is ![]() in wide, determine what the finished width would be in each of the following cases:
in wide, determine what the finished width would be in each of the following cases:
- if
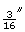 is planed off
is planed off - if
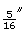 is planed off
is planed off
Solution
- From
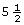 in on the scale, move
in on the scale, move 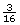 in to the left.
in to the left.

The final width, as shown on the ruler, is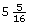 in.
in.
An alternate solution is to subtract.
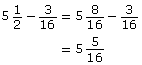
The planed width will be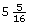 in.
in.
- From
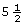 in on the scale, move
in on the scale, move 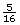 in to the left.
in to the left.

An alternate solution is to subtract.
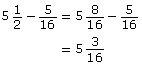
The planed width will be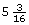 in.
in.
Did You Know?
Millions of trees are used every year just to make paper cups! Drinking from reusable containers makes sense.
Adding Feet and Inches
Example 6
A desk that is 2′9″ in width is pushed against a table measuring 5′6″. What is the total length in feet and inches?
Solution
One method of finding the solution is to convert everything to inches first.
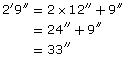
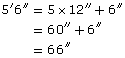
So,
![]()
Now change 99″ into feet and inches.
![]()
Because 8 × 12″ = 96″, 99″ = 8′3″.
Another method involves adding the feet and inches separately.
2′9″ + 5′6″ = 7′15″
![]()
So,
![]()
The total length of the desk and table pushed together is 8′3″.
 Self-Check
Self-Check
This is your opportunity to check your understanding. Answer the questions, and then check your answers.
SC 2. State each measure to the nearest fraction of an inch.




SC 3. One of the tallest women in the world is De-Fen Yao. She is 93 in tall. How tall is De-Fen Yao in feet and inches?
SC 4. The 2008 women’s Olympic record in pole vaulting is ![]() . What is this record in inches?
. What is this record in inches?
SC 5. Janice is cutting 1′3″ off a 7′ board. After the cut, what is the length of the board in feet and inches?
SC 6. Add 5′7″, 3′4″, and 6′5″.
Measuring with Yards

© Mikael Damkier/shutterstock
Have you played golf? Do you follow the PGA Tour? Golf courses in Canada and the United States still measure course distances in yards.
Professional golfers commonly drive golf balls 300 yards off the tee!
yard (yd): a unit of length in the imperial system
One yard equals 3 ft, or 0.9411 m.
The word yard comes from the Old English word gyrd, for stick! A yard is about the width of a front door, or the distance from your nose to the tips of your fingers when you stretch your arm to the side. A yard is also close to the length of an adult’s belt or the height of a kitchen stove.
Converting from Yards to Feet
Example 7
On the third hole at the local golf course, the distance from the tee to the green is 174 yd. How many feet is this distance?
Solution
![]()
Converting from Feet to Yards
Example 8
Jack’s driveway is 57 ft long. What is that distance in yards?
Solution
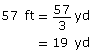
Jack’s driveway is 19 yd long.
mile (mi): a unit of length in the imperial system
The mile is defined today as exactly 5280 ft.
For longer distances, miles are used. A mile is longer than a kilometre. As a matter of fact, the mile is about 1.6 km. So, approximately how many kilometres would there be in 5 mi?
In the United States, distances between cities are posted in miles, and speeds are posted in miles per hour (mph). A speed of 100 km/h is about 60 mph.
Did You Know?
The mile originated in Ancient Rome. In Rome, two steps were called a passus. A passus was about five feet. One thousand passus was the Roman mile. The English word mile comes from the Latin word mille, which means 1000. About how many steps is 1 mi? 1 passus = 2 steps, so 1000 passus = 2000 steps—a good approximation even today for the mile!
Converting from Miles to Yards
Example 9
First Nations peoples who lived on the Plains, like the Cree and the Blackfoot, were nomadic and often travelled tens of miles a day. How many yards are there in a mile?
Solution
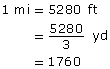
A mile is 5280 ft, or 1760 yd.
The multimedia tool “Imperial System Length Conversion” can be used to convert one unit of length in the imperial system to another unit. Move the left slider according to the unit you are starting with and the right slider to the unit you are converting to.
Use “Imperial System Length Conversion” to help summarize the conversion equivalents used so far in this lesson. Fill in the following blanks:
Use this multimedia tool to answer Example 9, which you have already tried answering. You may also use the tool to confirm your answers for the following Self-Check questions.
 Self-Check
Self-Check
Respond to the questions that follow.
SC 6.
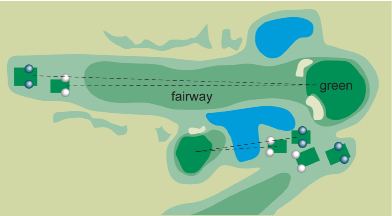
SC 7. On golf courses, white tees are placed a little closer to the green than the blue tees. If you are playing from the white tees, the Mountain View Golf Course in Whitehorse, Yukon, is 6114 yd long. How many miles long is that length? Round your answer to the nearest tenth of a mile.
SC 8. Marcie is driving to her friend’s farm. Her friend’s father said their house was a quarter mile off the main road. How many yards off the main road does Marcie’s friend live?
SC 9. A quarter section of land is a square one-half mile on each side. How many feet of fencing would be needed to fence a quarter section?
SC 10. A Canadian Football League field is 110 yd from goal line to goal line. How many feet is 110 yd?
SC 11. Barbara is fencing a quarter mile of pasture on her farm. If Barbara decides to use three strands of barbed wire, how many feet of wire will she need altogether?
proportion: a statement showing one ratio equal to another
For example, 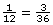 is a proportion statement.
is a proportion statement.
Because of trade and travel with the United States, which uses imperial measures for length and distance, more than tradespeople should be familiar with translating between systems—in fact, most Canadians should be able to translate between systems. Conversion is just a matter of using proportional reasoning—reasoning based on relations that can be represented by proportions.
Converting Between Imperial and Metric Units Using Proportions
Example 10
- Convert 1 ft to centimetres.
- Convert 1 ft to metres.
Solution
- You know that 1 in = 2.54 cm, and 1 ft = 12 in.
So, in 1 ft there will be 12 times as many centimetres as in 1 in.
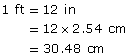
Of course, you could have used a proportion—two ratios equated to each other—to apply proportional reasoning more formally.
Let the number of centimetres in a foot be n.
Set up the proportion.

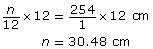
So, 1 ft = 30.48 cm.
- Since 1 m = 100 cm,
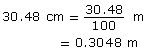
So, 1 ft = 0.3048 m.
Look at two more examples.
Converting Kilometres to Miles

iStockphoto/Thinkstock
Example 11
How many kilometres are there in 1 mi? Round your answer to 4 decimal places.
Solution
You know that 1 mi = 5280 ft and 1 ft = 0.3048 m.
So,
![]()
The following shows an alternate solution using a proportion.
To change miles to metres, use a proportion.
Let the number of metres in a mile be n.
Set up the proportion.

But 1 km = 1000 m.
So,

Therefore, 1 mi is about 1.6093 km.
Converting Metres to Yards
Example 12
Convert 1 m to yards. Round your answer to 4 decimal places.
Solution
You know that 1 m = 100 cm, 2.54 cm = 1 in, and 36 in = 1 yd.
Each of these equations has a unit in common. Therefore, you can use these equations to make the conversion into yards in this order: metres to centimetres; centimetres to inches; and, finally, inches to yards.
So,

 Self-Check
Self-Check
Respond to the following questions, and then check your answers.
SC 12. Complete a table like the following. Round your answers to 4 decimal places when necessary. Some of the entries have been done for you!
|
Metric |
Imperial |
|
1 mm |
________ in |
|
1 cm |
________ in |
|
1 m = 100 cm |
1.0936 yd |
|
1 km |
________ mi |
SC 13. Complete a table like the following. Round your answers to 4 decimal places when necessary. Some of the entries are done for you!
|
Imperial |
Metric |
|
1 in |
________ cm |
|
1 ft = 12 in |
30.48 cm or 0.3048 m |
|
1 yd = 3 ft = 36 in |
________ m |
|
1 mi = 5280 ft = 1760 yd |
1.6093 km |
Check your answers.
Next, you will use these tables to make conversions even simpler!
Converting Kilometres to Miles Using Tables
Example 13
The speed limit on the QE2 is 110 km/h. A friend has driven up from the United States. What would you tell him the speed limit is in miles per hour? Round your answer to the nearest mile per hour.
Solution
You must convert 110 km to miles.
From the tables, ![]() .
.
So,
![]()
A highway speed of 110 km/h is approximately 71 mph.
Example 14
Mei Lei’s house is on a lot 55 ft wide. What is the lot width in metres?
Solution
You must convert 55 ft to metres.
From the tables, 1 ft = 0.3048 m.
So,
![]()
Mei Lei’s lot is 16.764 m wide.
Your turn!
 Self-Check
Self-Check
Respond to the following questions. Then check your answers.
SC 14. A television screen measures 21 in on the diagonal. How many centimetres is the screen’s diagonal?
SC 15. Jack is 6 ft 2 in tall. What is his height to the nearest centimetre?
Did You Know?
The Red Pheasant First Nation is a Cree First Nation in Saskatchewan.
SC 16. The distance from Michael’s house to the Red Pheasant First Nation is 12.3 km. How far is this distance in miles? Round your answer to 1 decimal place.
 Try This
Try This
TT 11.
Use an SI (metric)–imperial conversion tool of your choice to do SC 14–SC 16 a second time.
 Mastering Concepts
Mastering Concepts
Try this question.
A carpenter wants to drill a hole through the centre of a board ![]() in wide. How far from each side should he drill?
in wide. How far from each side should he drill?
1.5. Page 5
Module 2: The Imperial System
Lesson Summary

© Feverpitch/shutterstock
Building a new home means reading, interpreting, and applying an architect’s plans. Framing carpenters must make careful measurements so everything fits together as intended. Measurements, even in modern construction, are often made using the imperial system.
In this lesson you explored the following questions:
- How are lengths and distances commonly measured in the imperial system?
- What is the history of length and distance units in the imperial system?
- How are imperial system units related?
- How are imperial system units applied in practical situations?
- How can units of length and distance be converted between the imperial and metric systems?
Check your level of understanding of the materials covered in this lesson by completing “Lesson 1 Traffic Lights.” If you select an amber or red traffic light in the multimedia piece, you will receive information about additional work you can complete to improve your understanding of the topics. Complete the suggested work before you proceed to the Lesson 1 Assignment. If you experience difficulty, contact your teacher before starting the Lesson 1 Assignment.
You discovered that the common units were the inch, foot, yard, and mile. You examined how these units are applied in situations and how one unit can be converted to another.
 Assignment
Assignment
Retrieve the Lesson 1 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment. Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Unit Project
Before you move on to the next lesson, you should start adapting your Unit 1 Project by applying the skills you mastered in this lesson. Start your second scale diagram by inserting imperial measures of length. For more information about this step and later steps of the Unit Project, refer to the Unit 1 Project.
1.6. Lesson 2
Module 2: The Imperial System
Lesson 2: Area
Focus

© Lepas/shutterstock
Does your project involve redecoration or renovation? New flooring? New carpets?
If you have wandered through a carpet outlet, you may have noticed that the price is often quoted by square metre and by square yard. Most often, the price per square yard is featured more prominently, since the price per yard is less than the price per metre. Regardless of whether you purchase your carpet by the square yard or by the square metre for a given area, you will pay the same amount.
One reason for working in the imperial system is that most carpet sold in North America is manufactured in 12-ft widths. How much would the carpet cost to cover a bedroom floor 9 ft × 12 ft if the carpet is advertised at $35.00 per square yard?
In this lesson you will explore the following questions:
- How are areas commonly measured in the imperial system?
- What is the history of area units in the imperial system?
- How are imperial system area units related?
- How are imperial system area units applied in practical situations?
- How can you convert between imperial area units and area units in the SI (metric) system?
Assessment
You will complete the Lesson 2 Assignment Booklet for assessment. Download the Lesson 2 Assignment Booklet and save it in your course folder now. You will receive instructions on how to complete the Assignment Booklet later in the lesson. You will also be prompted to start working on the Unit 1 Project.
Remember to save all activities, including those that are not part of the Assignment, in your course folder.
Required Materials and Equipment
You will need a ruler and a tape measure that show feet and inches, old newspapers, scissors, a marker, a calculator, and your estimation skills.
1.7. Page 2
Module 2: The Imperial System
Get Started
Did You Know?
The largest handwoven carpet is 60 m × 70 m, worth six million dollars, and used for prayer in Iran.
Which is easier—converting among units within the SI (metric) system or in the imperial system? Why? Most people find converting among units within the SI (metric) system easier. To convert among (SI) metric units, you just have to move the decimal to the left or right. SI (metric) units are defined in terms of powers of ten! But to convert among imperial units, you have to multiply or divide by numbers different from 10; for example, to convert miles to feet, you must multiply by 5280.
Most people use a calculator to convert among imperial measures. However, it is easy to make a mistake keying in the numbers or operations. To check if the answer your calculator displays is reasonable, you must use your estimation skills and a little mental arithmetic. These are skills you will use throughout your life—on the job, shopping, or around the home.
The next example may help you recall estimation skills you developed in previous math courses.
Example 1
Estimate the number of inches in 19 ft. Then calculate the exact answer carefully with a calculator to see if your estimate is reasonably accurate.
Solution
19 ft = 19 × 12 in
To estimate, round each number to the nearest ten.
19 rounds to 20 because 19 is closer to 20 than to 10.
12 rounds to 10 because 12 is closer to 10 than to 20.
So, 19 × 12 is about 20 × 10, or 200. In 19 ft, there are about 200 in.
This estimate makes sense, since the exact answer is 228 in!
This example illustrates how you can estimate products quickly in your head. First round each number so there is only one digit that is not zero. Then multiply the rounded values together. You can use this skill in the following Try This activity.
 Try This
Try This
In this activity you will apply estimation techniques. If possible, work with a partner.
Step 1: Use your calculator to help you change 39 mi to feet. Your answer should be 205 920 ft.
TT 1. Explain how you used your calculator to get this answer.
Step 2: Enter 39 × 580 in your calculator as if by mistake in converting from miles to feet.
TT 2. What does your calculator show?
TT 3. Explain how you would use your estimation skills to recognize that a mistake had been made.
 Share
Share
It’s time to share your answers to TT 1–TT 3. Remember that sharing work is an important part of learning. Use the following tips to ensure you get all the benefits from this sharing opportunity:
- Complete the questions to the best of your ability. Make sure your answers are in a form that you can easily share them with another student or with your teacher, if so directed.
- Use your class discussion area, or another method indicated by your teacher, to post your answers and to view the work of the people you’re sharing with.
- Compare your answers to the other posted answers. Identify where you have similar answers and where your answers are different. Discuss all differences between answers until you agree on the answers. If necessary, you may wish to involve your teacher in your discussion.
- Revise your answers where necessary.
Save a revised copy of your work in your course folder. Ask your teacher whether you should also save a summary of your discussion in your course folder.
Often, estimation is used to determine a product without requiring you to go to the work of finding the exact product using your calculator or a long-hand method. While you are developing your estimation skills, you can use the exact answer to confirm that you are estimating correctly. Calculating the exact answer allows you to confirm that your estimation skills are in good shape.
Once you have developed confidence in your estimation skills, you can use your estimated answers to judge whether a calculated answer is reasonable.
 Try This
Try This
For the following questions, discuss with a partner how you would estimate the first product. Write down your estimate. Then have your partner use a calculator to find the exact answer. Compare your estimates with the answers shown on the calculator. Reverse roles with each question.
TT 4. 31 × 5280
TT 5. 480 × 12
TT 6. 13 × 27
TT 7. 162.5 × 144
 Share
Share
It’s time to share your answers to TT 4–TT 7. Remember that sharing work is an important part of learning. Use the following tips to ensure you get all the benefits from this sharing opportunity:
- Complete the questions to the best of your ability. Make sure your answers are in a form that you can easily share them with another student or with your teacher, if so directed.
- Use your class discussion area, or another method indicated by your teacher, to post your answers and to view the work of the people you’re sharing with.
- Compare your answers to the other posted answers. Identify where you have similar answers and where your answers are different. Discuss all differences between answers until you agree on the answers. If necessary, you may wish to involve your teacher in your discussion.
- Revise your answers where necessary.
Save a revised copy of your work in your course folder. Ask your teacher whether you should also save a summary of your discussion in your course folder.
Now you should be ready to move on to the Explore part of the lesson.
1.8. Page 3
Module 2: The Imperial System
Explore

© Wieslaw Fila/Dreamstime
How do the square inch, square foot, and square yard compare to each other in size? This is what you will investigate next.
 Try This
Try This
You will need a ruler that shows inches, a tape measure that shows feet and inches, old newspapers, scissors, a marker, a calculator, and your estimation skills.
Work with a partner if possible. Later in the lesson, you will be asked to attach a copy of your responses to TT 8 to
TT 11 to your Assignment Booklet. Your responses to TT 8 to TT 11 will be marked as part of your Assignment Booklet.
From an old newspaper, cut out at least 13 identical squares. Each square must be one foot on each side. With your marker, write square foot on each square.
Next, arrange as many of these squares as is necessary to form a large square three feet on each side. Remember that three feet is equal to one yard.
TT 8. How many square feet are there in your arrangement? What might you call this large square area?
Take one of the square feet you cut out. From one corner, cut a small square that is 1 in on each side.
Fold the square foot so that, when it is unfolded, the creases show all the square inches in a square foot.






TT 9. How many square inches are there in a square foot? How did you arrive at your answer?
Finally, take 12 of your square feet and arrange them to form as many different rectangles as you can. Share the different ways the 12 square feet can be organized.
TT 10. Complete a table like the following for all of the rectangles you were able to make. For each arrangement, record the area and perimeter (the distance around).
|
Arrangement of Square Feet |
Area |
Perimeter |
|
|
12 ft2 |
16 ft |
|
|
|
|
|
|
TT 11. What did you notice about the rectangles, their areas, and their perimeters? Did you use the same words to describe perimeter and area?
Work with others to construct a statement that describes any relationship between the shape of rectangular objects, area, and perimeter.
 Share
Share
It’s time to share your answers to TT 8–TT 11. Remember that sharing work is an important part of learning. Use the following tips to ensure you get all the benefits from this sharing opportunity:
- Complete the questions to the best of your ability. Make sure your answers are in a form that you can easily share with another student or with your teacher, if so directed. You may find a digital camera handy to record arrangements.
- Use your class discussion area, or another method indicated by your teacher, to post your answers and to view the work of the people you’re sharing with.
- Compare your answers to the other posted answers. Identify where you have similar answers and where your answers are different. Discuss all differences between answers until you agree on the answers. If necessary, you may wish to involve your teacher in your discussion.
- When comparing answers for TT 10, make sure you have data for all the possible arrangements.
- Revise your answers where necessary.
Save a revised copy of your work in your course folder. Ask your teacher whether you should also save a summary of your discussion in your course folder.
1.9. Page 4
Module 2: The Imperial System
Bringing Ideas Together
Square Foot
Square Yard
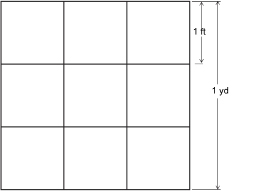
square inch (in2): a unit of area in the imperial system
A square inch is the area of a square 1 in on a side.
square foot (ft2): a unit of area in the imperial system
A square foot is the area of a square 1 ft on a side.
square yard (yd2): a unit of area in the imperial system
A square yard is the area of a square 1 yd on a side.
You have discovered that the squares having a side length of an inch, foot, or yard can be used as units of area. The related area units are square inch, square foot, and square yard.
As you discovered in Explore, 1 ft2 = 144 in2.
Why?
Also, you discovered 1 yd2 = 9 ft2.
Why?
Example 2
A wigwam, which is a semicircular structure originally made by First Nations people out of young tree saplings, has an interior close to the shape of a rectangle. The interior is 12 ft × 9 ft 3 in.
- What is the area of the wigwam in square feet? Estimate your answer first, and then calculate the exact answer.
- What is the area of the wigwam in square yards?
View the animated “Example 2 Solution.”
Example 3

© Stockbyte/thinkstock
Dawn bought wallpaper for her bedroom. The roll of wallpaper is ![]() in wide. Dawn’s walls are 8 ft high. She plans to cover the walls in vertical strips from floor to ceiling. What is the area that can be covered with one vertical strip of wallpaper?
in wide. Dawn’s walls are 8 ft high. She plans to cover the walls in vertical strips from floor to ceiling. What is the area that can be covered with one vertical strip of wallpaper?
Estimate first to predict an answer that would make sense.
Solution
Estimate first.
![]() in is just less than 24 in, or 2 ft.
in is just less than 24 in, or 2 ft.
An 8-ft strip, which is 2 ft wide, covers 8 ft × 2 ft, or 16 ft2.
Now use your calculator to determine the area more precisely.
You must first convert ![]() in to feet.
in to feet.
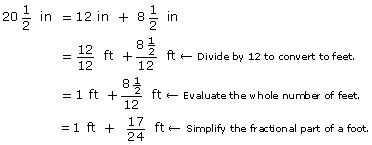
![]()
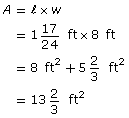
Each strip of wallpaper covers ![]() ft2.
ft2.
Try the following alternate solution using decimal values.
You must first convert ![]() in to feet.
in to feet.
![]()
Leave this answer on your calculator display.
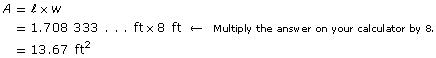
Each strip of wallpaper covers about 13.67 ft2 (which is approximately ![]() ft2).
ft2).
 Self-Check
Self-Check

© Baloncici /shutterstock
Respond to the questions that follow.
SC 1. Jasper wants to install a parquet floor in his kitchen. He sees an advertisement in a flyer that quotes prices per square foot. About how many square feet will Jasper need if the floor is a rectangle measuring 10 ft 9 in × 11 ft 6 in?
SC 2. A sheet of printer paper is 8.5 in × 11 in. Darcy says it is almost 1 ft2. Is Darcy correct? Explain your answer.
SC 3. Paula purchased a new home 1260 ft2 in area. What is the home’s area in square yards?
SC 4. Boris’s front lawn is rectangular and measures 50 ft × 30 ft. He purchased a fall fertilizer that must be applied at a rate of 6 lb per 1000 ft2. How many pounds of fertilizer should Boris apply?
Did You Know?
A moccasin is a shoe made by First Nations people out of deer leather.
SC 5. The sole of each of Norma’s moccasins is 36 in2 in area. When Norma stands with both feet flat on the floor, what is the total area in square feet that the moccasins cover?
SC 6. How many square inches are there in 1 yd2?
Beyond the Square Yard
Do you remember the units used in the SI (metric) system for describing larger areas, such as the area of a field or even the area of a province?
In the imperial system the acre and square mile are used to describe areas too large to be easily described by the square foot or square yard.

© Kurt De Bruyn/shutterstock
acre (ac): a unit of area in the imperial system
An acre is 22 yd wide by 220 yd long or 4840 yd2.
square mile (mi2): a unit of area in the imperial system
A square mile is the area of a square 1 mi on a side.
Did You Know?
The year 2009 was the year of the ox in Chinese culture. People born during this year are said to be reliable, patient, and hard working.
The acre was originally defined as the area of a field that could be ploughed by a single ox in one day. The word acre comes from the Old English word aecer, meaning field.
In the last half day of the nineteenth century, surveyors mapped Western Canada. The land was divided into squares that measured 6 mi on a side. These large squares were called townships.
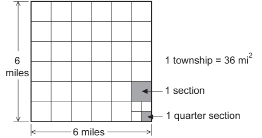

© 2007 Leigh Spicer. All rights reserved.
A square mile was called a section, so there were 36 sections in a township. Each section was divided into quarters, or quarter sections. Each quarter section was one-half mile. These quarter sections were parcelled out as homesteads. Each quarter section was 160 ac in size. An acre, an imperial area measurement, is a square that measures approximately 70 yd on a side.
Today you can see evidence of this survey from the air. North-south roads in the country are 1 mi apart.
East-west roads are 2 mi apart. Seen from the air, the roads divide the countryside into rectangles measuring 1 mi by 2 mi in size. Each of these rectangles is two sections!
Example 4

© Yobro10/Dreamstime
An American football field is 360 ft × 160 ft. Is its area much smaller than, roughly the same as, or much larger than 1 ac?
Solution
Compare the area of the football field to an acre, 4840 yd2.
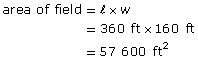
Convert this area to square yards. Recall, that 1 yd2 = 9 ft2.
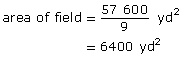
An American football field is roughly 1 ac in area. In fact, it is 1.3 times larger than an acre, as you can see from this calculation.
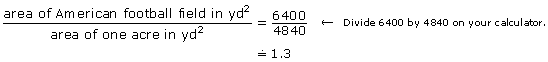
You can use the interactive multimedia “Imperial System Area Conversion” to confirm the solution to the previous example.
You may also use this interactive to help you complete the Self-Check questions that follow.
 Self-Check
Self-Check
Respond to the following questions.

© Bronwyn Photo/shutterstock
SC 7. There are 160 ac in a quarter section. How many acres are there in a section that is 1 mi2 in area?
SC 8. When the Doukhobors immigrated to Canada from Russia in 1899, they were granted 773 400 ac for their farms and communities in what is now Saskatchewan and Manitoba. What is the area of this land grant in square miles?
SC 9. According to the United States Department of Agriculture, in 2009, American farmers planted 320.9 million acres to principal crops. What is this acreage in square miles?
SC 10. Using your answer from question 9, how long would the sides of a square be that enclosed 320.9 million acres? Express your answer to the nearest mile.
How do you find the side length of any square from its area? For example, what is the side length of a square having an area of 9 mi2?
It is often necessary to convert areas between the SI (metric) and imperial systems.
Example 5
Convert 1 in2 to square centimetres.
Solution
1 in = 2.54 cm
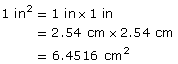
Remember that when you were working with linear measurements, you created tables to help convert between the SI (metric) and imperial measurement systems. As you will see in the next questions, you can do the same thing for area measurements.
 Self-Check
Self-Check
Respond to the following questions.
SC 11. Complete a table like the following. Round to 4 decimal places when necessary. Two examples have been done for you.
|
Imperial |
Metric |
|
1 in2 |
6.4516 cm2 |
|
1 ft2 |
________ m2 |
|
1 yd2 |
________ m2 |
|
1 ac |
0.4047 ha |
|
1 mi2 |
________ km2 |
SC 12. Complete a table like the following. Round to 4 decimal places when necessary. Two have been done for you.
|
Metric |
Imperial |
|
1 cm2 |
________ in2 |
|
1 m2 |
________ ft2 |
|
1 m2 |
________ yd2 |
|
1 ha |
2.4711 ac |
|
1 km2 |
0.3861 mi2 |
The tables you completed in SC 11 to SC 12 may help you simplify conversions between systems.
Example 6
The area of Jasper’s living room is 180 ft2. What is the area in square metres?
Solution
![]()
So,
![]()
The living room area is about 16.722 m2.
 Self-Check
Self-Check
Do the following questions. Use the information from the tables in SC 11 to SC 12.
SC 13. Nick planted 320 ac of canola. How many hectares of canola did he plant? Round your answer to 1 decimal place.
SC 14. The area of Morris’s front lawn is 100 yd2. What is the area in square metres? Round your answer to the nearest unit.
SC 15. The printed area of a wedding invitation is 150 cm2. What is the area in square inches? Round your answer to 1 decimal place.
You may wish to do SC 13 to SC 15 a second time using a conversion tool found on the Internet.
 Mastering Concepts
Mastering Concepts
Try this question.
In 2009, in Canada, about 141 000 new homes were constructed. If the average size of each home were 1800 ft2 in area, how many square miles of new homes does this represent? Express your answer to the nearest square mile.
1.10. Page 5
Module 2: The Imperial System
Lesson Summary

© AVAVA/shutterstock
The cost of flooring when building a new home depends on the area that has to be covered. You may have noticed that stores often quote prices for hardwood, linoleum, tile, carpet, and other forms of flooring in dollars per square foot or square yard. The square foot and square yard are imperial units of area.
In this lesson explored the following questions:
- How are areas commonly measured in the imperial system?
- What is the history of area units in the imperial system?
- How are imperial system area units related?
- How are imperial system area units applied in practical situations?
- How can you convert between imperial area units and area units in the SI (metric) system?
Check your level of understanding of the materials covered in this lesson by completing “Lesson 2 Traffic Lights.” If you select an amber or red traffic light in the multimedia piece, you will receive information about additional work you can complete to improve your understanding of the topics. Complete the suggested work before you proceed to the Lesson 2 Assignment. If you experience difficulty, contact your teacher before starting the Lesson 2 Assignment.
You discovered that common imperial units of area included the square inch, square foot, and square yard. In the SI (metric) system, larger areas are described using hectares and square kilometres. In the imperial system, you found that the acre and square mile were used for larger areas.
Assignment
Retrieve the Lesson 2 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment. Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Unit Project
Before you move on to the next lesson, you should start to address the area components in the Unit 1 Project by applying the skills you mastered in this lesson. For more information about this step and later steps of the Unit Project, refer to the Unit 1 Project description.
1.11. Lesson 3
Module 2: The Imperial System
Lesson 3: Volume and Capacity
Focus

© Jonathan Larsen/shutterstock
Modern home design incorporates energy conservation. What could you do in your own home to minimize energy consumption?
Marlene and her class are discussing ways people can reduce the amount of energy used in their homes. One student’s suggestion was to turn down the thermostat to a cooler, but still comfortable, temperature.
Marlene added that in her home, her mother installed a thermostat that automatically changes the setting to a cooler temperature at night when everyone in the home is asleep. Marlene said her mother monitored the amount of natural gas the family used to heat their home this February as compared to previous years, and the family noticed a significant saving.
When the teacher asked Marlene how much natural gas they used in February, Marlene said her mom reads the gas meter at the beginning and end of the month. This year, in February, Marlene’s family only used 20 000 cubic feet—almost 1800 cubic feet less than last year!
Peter interrupted, “Cubic feet? What’s a cubic foot? We don’t use feet and inches very often.” The teacher replied that the cubic foot is a unit of volume in the imperial system, and many gas meters still measure the volume of gas consumed in that unit.
Then the class turned to how much 20 000 cubic feet was and how many times you could fill the classroom with 20 000 cubic feet of air!
In this lesson you will explore the following questions:
- How are volumes and capacity commonly measured in the imperial system?
- What is the history of volume and capacity units in the imperial system?
- How are volume and capacity units in the imperial system related?
- How are volume and capacity units in the imperial system applied in practical situations?
Assessment
You will complete the Lesson 3 Assignment Booklet for assessment. Download the Lesson 3 Assignment Booklet and save it in your course folder now. You will receive further instructions on how to complete the Assignment Booklet later in this lesson.
Remember to save all activities, including those that are not part of the Assignment, in your course folder.
Required Materials and Equipment
You will need a ruler, a tape measure that shows feet and inches, and your estimation skills.
1.12. Page 2
Module 2: The Imperial System
Get Started
In the last lesson you explored estimating answers to multiplication questions. You will remember that your estimation skills are important in seeing whether or not an answer given to a problem seems reasonable.
When working with units in the imperial system, you often multiply or divide by numbers that are difficult to handle mentally. Are there estimation techniques for division that make this task simpler?
The following example shows an estimation technique that relies on rounding each number to numbers that will easily divide into each other.
Example 1

iStockphoto/Thinkstock
Consider the following division question:
217 ÷ 27
Use your calculator. What is the answer to this question?
How could you estimate this answer without a calculator?
Solution
Begin by rounding 27 to one non-zero digit. What is this rounded value?
Next you should round the number being divided, 217, to two non-zero digits.
Why should you choose to round to two digits rather than one?
But the 2 in 200 is not divisible by the 3 in 30 a whole number of times. So instead, 217 is rounded to 210 because the 21 in 210 is divisible by the 3 in 30 a whole number of times.
Why wouldn’t you round 217 to 220 instead?
What is 21 ÷ 3?
What is 210 ÷ 30?
So, the estimated value of 217 ÷ 27 = 7, which is close to the value recorded from your calculator.
compatible numbers: numbers that are easy to use in a mental computation, especially division
You just used compatible numbers to estimate the answer to a division question.
For example, the numbers 21 and 3 are compatible numbers because 3 divides into 21 a whole number of times.
Example 2
Suppose the following numbers are to be used in a division. Which of the following numbers are compatible numbers?
- 32 and 7
- 15 and 5
- 44 and 11
- 40 and 6
Solution
- 7 does not divide into 32 a whole number of times, so these numbers are not compatible.
- 15 and 5 are compatible because 15 ÷ 5 = 3.
- 44 and 11 are compatible because 44 ÷ 11 = 4.
- 6 does not divide into 40 a whole number of times, so these numbers are not compatible.
 Self-Check
Self-Check
Respond to the following questions.
SC 1. Estimate 35 146 ÷ 41.
 Try This
Try This
Solve the following equations, first using estimation and then using calculation.
TT 1. 6700 ÷ 301 =
TT 2. 3758 ÷ 513 =
TT 3. 916 ÷ 22.7 =
TT 4. 81 070 ÷ 403.98 =
 Share
Share
It’s time to share your answers to TT 1–TT 4. Remember that sharing work is an important part of learning. As you discuss the Try This questions with a partner, think about the compatible numbers you used in the TT questions.
- Did your estimates differ from your partner’s estimates?
- Did you choose the same compatible numbers as your partner chose?
- Compare your estimates with the answers on a calculator.
- Why were some estimates closer to the calculated answers than others?
Revise your answers where necessary. Summarize your discussion by explaining how choosing different compatible numbers can lead to a variety of different estimates.
Save a revised copy of your work and a summary of your discussion in your course folder.
Now you should be ready to begin the Explore part of this lesson.
1.13. Page 3
Module 2: The Imperial System
Explore
When you double the dimensions of a rectangle, you increase the rectangle’s area not by a factor of 2, but by a factor of 4.
For example, if you have a mat measuring 2 ft × 3 ft, the mat’s area is 6 ft2. If you double its dimensions, it becomes a mat with the measurements of 4 ft × 6 ft. The area of this larger mat is 24 ft2. This larger mat has an area four times the smaller mat.
What happens to the volume of something when its dimensions are increased by a factor? You will investigate this question in the next activity.
 Try This
Try This
In this activity you will investigate the effect increasing all three dimensions of your bedroom has on your bedroom’s volume.
You will need a ruler or tape measure that shows feet and inches and your estimation skills.
Do you remember the formula used to calculate the volume of a rectangular, prism-shaped object?
Work with a partner if possible.

iStockphoto/Thinkstock
Measure the length, width, and height of your bedroom. Round each dimension to the nearest foot.
TT 5. Record these dimensions and calculate the volume.
TT 6. How would you calculate the number of cubes (1 ft on each side) needed to fill your bedroom? How do you think the volume of air in your bedroom relates to the number of cubes? Explain your reasoning.
TT 7. Double each dimension of your bedroom. Record these new dimensions. Now calculate the volume of a room with these dimensions. How many times has the volume increased?
TT 8. Next, triple the dimensions of your bedroom. Calculate the volume of such a room. Compare this volume with the original volume of your room. Once again, how many times has the volume increased?
TT 9. What is the relationship between the new volumes and the number of times you increased the dimensions?
 Share
Share
It’s time to share your answers to TT 5–TT 9. Remember that sharing work is an important part of learning. Use the following tips to ensure you get all the benefits from this sharing opportunity.
- Complete the questions to the best of your ability. Make sure your answers are in a form that you can easily share with another student or with your teacher, if so directed.
- Use your class discussion area, or another method indicated by your teacher, to post your answers and to view the work of the people you’re sharing with.
- Compare your answers to the other posted answers. Identify where you have similar answers and where your answers are different. Discuss all differences between answers until you agree on the answers. If necessary, you may wish to involve your teacher in your discussion.
- Revise your answers where necessary.
Save a revised copy of your work in your course folder. Ask your teacher whether you should also save a summary of your discussion in your course folder.
V = l × w × h, where l is the length, w is the width, and h is the height.
1.14. Page 4
Module 2: The Imperial System
Bringing Ideas Together
cubic foot (ft3): a unit of volume in the imperial system
A cubic foot is the volume of a cube having an edge length of 1 ft.
cubic inch (in3): a unit of volume in the imperial system
A cubic inch is the volume of a cube having an edge length of 1 in.
cubic yard (yd3): a unit of volume in the imperial system
A cubic yard is the volume of a cube having an edge length of 1 yd.
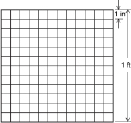
In the Explore you calculated the volume of your bedroom in cubic feet. The following cube is 1 cubic foot.
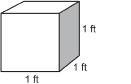
A basketball is almost 10 in in diameter. How many inches are in 1 ft?
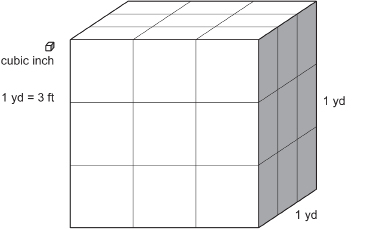
There are two other common units: the cubic inch and the cubic yard. Cubes representing these units of volume are shown in the diagram.
As you discovered in Explore, if the dimensions of a rectangular box are increased by a factor of 3, the volume of the larger box is 3 × 3 × 3, or 27 times, as much as before.
So, it’s not surprising that 1 yd3, as a volume, is 27 times as much as 1 ft3.
You can also see this relation between cubic yards and cubic feet by applying the formula ![]() to the same cube—once using measurements in yards and once using measurements in feet.
to the same cube—once using measurements in yards and once using measurements in feet.
![]()
and
![]()
So, 1 yd3 = 27 ft3.
Garden oil, concrete, sand, and gravel are often sold by the cubic yard.
The Cubic Foot
The cube represents the volume of 1 ft3. The cube faces have grid lines separated by 1 in. The grid lines can help you figure out how many cubic inches are in 1 ft3.
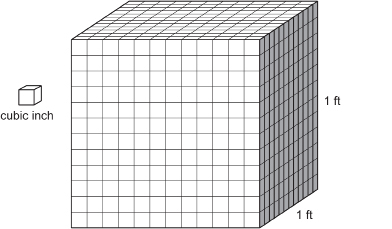
How many cubic inches are there in a cubic foot?
There is another way to understand how many cubic inches there are in a cubic foot. Going from 1 in3 to 1 ft3 you are increasing each of the three dimensions by a factor of 12. Therefore, the volume will increase by 12 × 12 × 12. So, the volume will increase by a factor of 1728.
In terms of volume, 1 ft3 is certainly much larger than 1 in3.

Stockbyte/Thinkstock
Example 3
A tissue box is 5 in wide, 9 in long, and 3 in high.
- What is the volume of the box in cubic inches?
- What is the volume of the box in cubic feet?
Express your answer as a fraction or decimal value. If using a decimal value, round your answer to 2 decimal places.
Solution
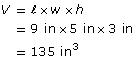
The volume of the tissue box is 135 in3.
- Method 1
Change each dimension to feet first, since the answer is required in cubic feet.
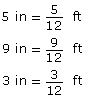
Now find the volume. Because the dimensions are in feet, your answer will be in cubic feet.
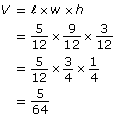
The volume is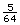 ft3.
ft3.
To express the volume in decimal form, you could continue this way.
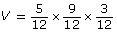
On your calculator, press
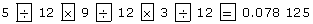
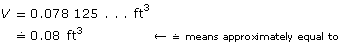
To round to 2 decimal places, look at the third decimal place. If the digit is 5 or more, round up!
The volume is 0.08 ft3.
Method 2
Convert cubic inches to cubic feet directly, since the volume is already calculated in cubic inches.
1 ft3 = 1728 in3
So,
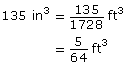
The volume is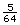 ft3.
ft3.
To express the volume in decimal form, you could continue in the following way.
On your calculator, press

To round to 2 decimal places, look at the third decimal place. If the digit is 5 or more, round up!
To check if 0.08 ft3 is reasonable, estimate ![]() using compatible numbers.
using compatible numbers.
Round 1728 to 2000.
Round 135 to 140. Do you agree 14 and 2 are compatible numbers?
The volume is 0.08 ft3.
Example 4
Chuck ordered 4 yd3 of soil to raise the level of the flower beds along his house. How many cubic feet of soil did Chuck order?
Solution
Because 1 yd3 = 3 ft × 3 ft × 3 ft = 27 ft3,
![]()
Try using “Imperial System Volume Conversion” to check the unit conversions in the previous examples.
 Self-Check
Self-Check
Respond to the following questions. When you are finished, check your answers using “Imperial System Volume Conversion,” the conversion tool you used to check the Example answers.
Did You Know?
With 1183 horsepower, the SSC Ultimate Aero TT is the world’s most powerful car.
SC 2. Connie is interested in classic cars. At a recent auto show, she saw a 1981 Ford Mustang 4.6 on display. The engine displacement was given as 281 in3. She was told that was the same as saying the car had a 4.6-L engine. What is the engine displacement in cubic feet?
Round your answer to 2 decimal places.
SC 3. A cardboard box is 24 in long, 18 in wide, and 18 in high.
- What is the volume of the box in cubic feet?
- What is the volume of the box in cubic yards?
SC 4. Give an example of an everyday object that has each of the following volumes.
- 1 in3
- 1 ft3
- 1 yd3
SC 5. Six inches of fresh snow fell on Blaine’s driveway, which is 60 ft long and 18 ft wide.
- How many cubic feet of snow must Blaine move to clear his driveway?
- How many cubic yards of snow must Blaine move to clear his driveway?
Units of Capacity
Do you remember the units commonly used in the metric system for capacity? What are they?
The imperial units of capacity include the fluid ounce, cup, pint, quart, and gallon. There are ![]() cups in a pint, 2 pints in a quart, and 4 quarts in a gallon.
cups in a pint, 2 pints in a quart, and 4 quarts in a gallon.

© Geoffrey Kuchera/shutterstock
pint (pt): a measure of capacity in the imperial system
A pint is roughly equal to 0.5 L.
quart (qt): a measure of capacity in the imperial system
There are 2 pt in a quart.
A quart is approximately equal to 1 L.
gallon (gal): a measure of capacity in the imperial system
A gallon is 4 qt in size.
|
1 fluid ounce |
1 cup = 8 fluid ounces |
|
1 pint = |
1 quart = 2 pints |
|
1 gallon = 4 quarts |
|

© Elena Ray/shutterstock
An imperial quart is slightly larger than a litre. An imperial quart is 1.14 L.
In the United States, milk and juice are commonly sold in gallon, quart, and pint containers. Americans buy gasoline by the gallon.
Did You Know?
Milk in Ontario is also sold in bags, not just jugs or rigid containers.
However, these United States’ measures are different from what they are in Canada. The American quart and gallon are only ![]() as large as their Canadian imperial equivalents.
as large as their Canadian imperial equivalents.
Inconsistencies such as these are good reasons to use metric units to quote volumes and capacities!
If you have done a little baking, you have probably encountered the cup and the fluid ounce in older recipes. There are 160 fluid ounces in an imperial gallon and 40 fluid ounces in an imperial quart. You may see ounces on imported goods.
The word gallon comes from the Latin word galleta. Galleta is the Latin word for pail. A four-litre pail of ice cream holds about one gallon.
Example 5
René’s cousin in Seattle is painting the bedrooms in his home. He calculated that he needs enough paint to cover 900 ft2. How many gallons should he buy if 1 qt covers 75 ft2?
Solution
1 gal = 4 qt
1 qt of paint covers 75 ft2.
So, 1 gal covers 4 × 75 ft2 = 300 ft2.
![]()
René’s cousin needs to buy 3 gal of paint.
Example 6
Marlene bought 1 gal of orange juice while travelling in Montana.
- How many cups of juice are there in Marlene’s gallon of juice?
- If one serving of juice is one-third of a cup, how many servings are there in Marlene’s gallon of juice?
Solution
- 1 gal = 4 qt
1 qt = 2 pt
So, there are 4 × 2 = 8 pt in 1 gal.
1 pt = 2 c
So, there are 8 × 2 = 16 c of juice in 1 gal.
- 1 c = 3 servings
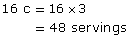
There are 48 servings of juice.
 Self-Check
Self-Check
Try the following questions.
SC 6. When travelling in North Dakota, Mary bought a gallon of milk for $3.00. How many quarts are in 1 gal? Calculate how much each quart cost.
SC 7. Bill wants to paint the exterior of his garage door. The garage door measures 16 ft × 7 ft. He has 2 qt of paint left in a gallon container he purchased earlier. Will Bill have enough paint for this project if the directions on the gallon container say the container holds enough paint to cover 250 ft2?
Imperial and American Standard Measures of Capacity
As for length and area, tables may be used to convert between metric measures and volume measures, such as cubic inches, cubic feet, cubic yards, quarts, and gallons. However, the situation for volume is complicated by the fact that, in the United States, the units for capacity (such as quarts and gallons) are not the same as the imperial equivalents. The American gallon is very close to 4 L, but the imperial gallon is 20% larger. This creates confusion when talking about fuel consumption, for instance. Twenty miles per gallon does not mean the same thing in Canada as it does in the United States.
Did You Know?
Canada is the largest provider of oil and natural gas for the United States.
Before looking at the conversion tables for metric, imperial, and American Standard measures, work through the following example to see how entries in the tables are obtained.
Example 7
How many cubic centimetres are there in 1 in3?
Solution
Remember that 1 in = 2.54 cm.
So,
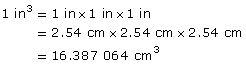
There are exactly 16.387 064 cm3 in 1 in3.
Look at the following conversion tables. The entries have been rounded.
|
Metric |
Imperial (Canadian) |
American Standard Measures |
|
1 cm3 |
0.0610 in3 |
0.0610 in3 |
|
1 m3 |
1.3080 yd3 |
1.3080 yd3 |
|
1 m3 |
35.3147 ft3 |
35.3147 ft3 |
|
1 L |
0.2200 gal |
0.2642 gal (US) |
|
1 L |
0.88 qt |
1.0567 qt (US) |
|
Imperial |
American Standard Measures |
Metric |
|
1 in3 |
1 in3 |
16.3871 cm3 |
|
1 ft3 |
1 ft3 |
0.0283 m3 |
|
1 yd3 |
1 yd3 |
0.7646 m3 |
|
1 qt |
1.2010 qt (US) |
1.1366 L |
|
1 gal |
1.2010 gal (US) |
4.5465 L |
|
American Standard Measures |
Imperial |
Metric |
|
1 qt (US) |
0.8327 qt |
0.9462 L |
|
1 gal (US) |
0.8327 gal |
3.7854 L |
Work through the following examples to see how to use these tables.
Example 8

iStockphoto/Thinkstock
Bernice is ordering topsoil for her garden. She calculated she needs 15 yd3. When she telephones in her order, how many cubic metres should she ask for? Round your answer to 1 decimal place.
Solution
![]()
So,
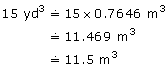
Bernice should order 11.5 m3 of topsoil.
Example 9

iStockphoto/Thinkstock
A compact car in the United States is advertised as averaging 32 mi/gal. How many miles to the imperial gallon would the car average?
Solution
A Canadian gallon is larger than a US gallon.
1 gal (imp) = 1.2010 gal (US)
So, the car would go 1.2010 farther on an imperial gallon.
1.2010 × 32 mi = 38.432 mi
On an imperial gallon, the mileage would be 38.432 mi/gal.
 Self-Check
Self-Check
Try the following questions.
SC 8. How many litres of paint are there in 5 gal (imp)?
SC 9. Bill bought 3 qt of milk in Montana, US. How many litres of milk did Bill buy?
SC 10. If gasoline sells for $0.936 per litre, how much is it per imperial gallon? Round your answer to the nearest cent.
SC 11. How many cubic feet are there in a load of concrete 2 m3? Round your answer to 1 decimal place.
 Mastering Concepts
Mastering Concepts
Aaron wants to order enough topsoil to raise a rectangular flower bed 8 in. If the flower bed measures 21 ft × 3 ft, how many cubic yards of topsoil should he order if the landscape firm sells soil to the nearest one-half cubic yard? Make sure Aaron is not short on topsoil!
![]()
So, 0.08 is a reasonable answer.
You can count the number of cubic inches making up the cubic foot. Clearly, the top layer contains 144 cubic inches. There are 12 layers. So, there are 12 × 144 in3 in all.
So, there are 1728 in3 in a cubic foot.
You can also calculate the number of cubic inches using the formula ![]() .
.
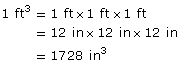
1.15. Page 5
Module 2: The Imperial System
Lesson Summary

© Jim Parkin/shutterstock
Natural gas from western Canada flows through pipelines to markets across North America. Consumers are billed based on the amount of gas they use. If your home uses natural gas for heating, ask to see last month’s bill to find out how much natural gas your home used. The volume of natural gas you consumed was most likely quoted in thousands of cubic feet and then converted to an energy equivalent. The cubic foot is a measure of volume in the imperial system.
In this lesson you explored the following lesson questions:
- How are volumes and capacity commonly measured in the imperial system?
- What is the history of volume and capacity units in the imperial system?
- How are volume and capacity units in the imperial system related?
- How are volume and capacity units in the imperial system applied in practical situations?
Check your level of understanding of the materials covered in this lesson by completing “Lesson 3 Traffic Lights.” If you select an amber or red traffic light in the multimedia piece, you will receive information about additional work you can complete to improve your understanding of the topics. Complete the suggested work before you proceed to the Lesson 3 Assignment. If you experience difficulty, contact your teacher before starting the Lesson 3 Assignment.
 Assignment
Assignment
Retrieve the Lesson 3 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment. Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Unit Project
Before you move on to the next lesson, you should start to address the volume components in the Unit 1 Project by applying the skills you mastered in this lesson. For more information about this step and later steps of the Unit Project, refer to the Unit 1 Project.
1.16. Lesson 4
Module 2: The Imperial System
Lesson 4: Weight
Focus

© Robyn Mackenzie/shutterstock
Does your project involve redesigning a kitchen space in your home? How would you plan for storage? For food preparation?
Munir is making a batch of cookies. He is using a favourite recipe from his grandmother’s cookbook. The recipe calls for two ounces of fresh butter. He asks his sister for advice. Listen in.
“How much butter is two ounces?” asked Munir.
“I think ounces are parts of a pound,” his sister answered.
“Well,” Munir complained,” I just bought this brick of butter and all it says on the wrapping is 454 g. Now what?”
How would you help Munir add the correct amount of butter?
In this lesson you will explore the following questions:
- How are weights (masses) commonly measured in the imperial system?
- What is the history of units for mass in the imperial system?
- How are the units for weight in the imperial system related?
- How are the units for weights in the imperial system applied in practical situations?
- How are masses (weight) converted between the imperial and SI units?
Assessment
You will complete the Lesson 4 Assignment Booklet for assessment. Download the Lesson 4 Assignment Booklet and save it in your course folder now. You will receive further instructions on how to complete the Assignment Booklet later in this lesson. Remember to save all activities, including those that are not part of the Assignment, in your course folder.
Required Materials and Equipment
You will need access to scales to weigh a variety of items. You will also need your calculator.
1.17. Page 2
Module 2: The Imperial System
Get Started
Many people still think in pounds when stating their weight or buying produce in a supermarket. But how good are they at estimating weight in pounds?

© Rob Wilson/shutterstock
Have you ever travelled by air? If you have, you know that airlines have restrictions about checked baggage. For example, some airlines limit passengers travelling in their economy class to two checked bags, and neither bag can exceed 50 pounds. If passengers check more bags or if their bags are too heavy, the passengers are charged a penalty.
How would you decide if one of your suitcases weighed 50 pounds?
 Try This
Try This
In this activity you will test your skills in estimating weight in pounds!
Work with a partner if possible. You will need a bathroom scale and an empty suitcase or box.
Caution: Do not try to handle more weight than you can safely lift.
Fill the suitcase with items such as books or canned goods until when you lift the suitcase or box you think it weighs 50 pounds.
Now check the weight on the scale.
What could you do to weigh the suitcase if it doesn’t balance on the scale? One method is to weigh yourself first. Then stand on the scale carrying the suitcase. Subtract your weight from your weight when holding the suitcase. The difference is the weight of the suitcase!
Add or subtract items until you have a 50-pound suitcase!
TT 1. How good were you in estimating weight?
TT 2. If you were going on a holiday, would you trust an estimate without weighing your suitcase—especially if you were going to be charged extra money if you were over the weight limit?
 Share
Share
It’s time to share your answers to TT 1–TT 2. Remember that sharing work is an important part of learning. Use the following tips to ensure you get all the benefits from this sharing opportunity:
- Complete the questions to the best of your ability. Make sure your answers are in a form that you can easily share with another student or with your teacher, if so directed.
- Use your class discussion area, or another method indicated by your teacher, to post your answers and to view the work of the people you’re sharing with.
- Compare your answers to the other posted answers. Identify where you have similar answers and where your answers are different. Discuss all differences between answers until you agree on the answers. If necessary, you may wish to involve your teacher in your discussion.
- Revise your answers where necessary.
Save a revised copy of your work in your course folder. Ask your teacher whether you should also save a summary of your discussion in your course folder.
1.18. Page 3
Module 2: The Imperial System
Explore
Work with a partner if possible.
 Try This
Try This
TT 3. Complete a table like the one shown in TT 4 by selecting at least two items for each of the target weights. Do not weigh the selected items yet.
Caution: Do not try to handle more weight than you can safely lift.
TT 4. Check the accuracy of this list by weighing the items on your scale and recording their weights in your table.
|
Target Weight (pounds) |
Item 1 |
Item 2 |
||
|
Selected Item |
Measured Weight (lb) |
Selected Item |
Measured Weight (lb) |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
5 |
|
|
|
|
|
10 |
|
|
|
|
|
20 |
|
|
|
|
|
50 |
|
|
|
|
|
100 |
|
|
|
|
TT 5. Discuss how you selected these items.
TT 6. How important are scales to measure weight?
 Share
Share
It’s time to share your answers to TT 3–TT 6. Remember that sharing work is an important part of learning.
Post your chart to the discussion board. Then add onto your chart by including the contributions of at least two other students. Be sure to thank the students whose contributions you used!
Include the enlarged chart as part of your answers to the Try This questions. Save a revised copy of your work in your course folder. Ask your teacher whether you should also save a summary of your discussion in your course folder.
1.19. Page 4
Module 2: The Imperial System
Bringing Ideas Together
pound (lb): a unit of weight (mass) in the imperial system
One pound is defined as exactly 0.453 592 37 kg.
In Explore and Get Started you weighed items in pounds. The pound as a unit of weight dates back at least as far as the time of the Romans. As a matter of interest, the symbol for one pound is 1 lb. This symbol is an abbreviation of the Latin word libra—the word for a set of scales used for weighing.

© Glam/shutterstock
Did You Know?
The symbol for the birth sign Libra is a set of scales! The constellation Libra is thought to look like a set of scales.

© EdBockStock/shutterstock
Nowadays, a set of scales is considered to be any instrument that measures weight (mass). An instrument that measures weight does not have to be made up of two pans connected to a bar. For example, bathroom scales are often compact devices that have a spring-loaded platform that moves down in response to the weight on it.
A pound is about half a kilogram. Look at the wrapping on a pound of butter. You will recall that Curtis read that the brick of butter was 454 grams. Is 1 lb more or less than one-half kilogram? Because 0.5 kg = 500 g, 1 lb is less than 0.5 kg.
Did You Know?
The Roman pound was divided into 12 parts. The Latin word uncia for “twelfth part,” as you will recall, gave the word inch. It also gives the English word ounce.
The troy pound, used for precious metals, such as gold and silver, still has 12 ounces. However, the modern pound commonly used for weight (mass) is divided into 16 ounces!
ounce (oz): a unit of weight (mass) in the imperial system
There are 16 oz in 1 lb.
1 lb = 16 oz
The following examples deal with the relationship between pounds and ounces.
Example 1
Nutritionists recommend active teenage girls eat 5 oz of protein each day. How many pounds of protein would this recommendation be over a 30-day month?
Solution
Now convert ounces to pounds. Remember 1 lb = 16 oz.
![]()
The recommended monthly protein requirement is 9.375 lb.
Example 2
Krysta’s baby was 6 lb 7 oz when she was born. Altogether, how many ounces did the newborn weigh?
View the animated “Example 2 Solution.”
It’s time to weigh your skills.
 Self-Check
Self-Check
Respond to the following questions.
SC 1. An average egg weighs about 2 oz. How much would two dozen eggs weigh?
SC 2. A butcher slices a 5-lb ham into 160 pieces. What is the average weight in ounces per slice?
SC 3. Emile’s cat has 7 kittens. Each kitten weighs 3 oz. What is their total weight in pounds and ounces?
SC 4. Victor and his friends caught 30 perch. The total catch weighed 15 lb. On average, how many ounces did each perch weigh?

© Bram van Broekhoven/shutterstock
What unit did you use in the metric system for large masses such as the mass of a load of sand? Large masses were measured in tonnes. 1 t = 1000 kg
In the imperial system, large weights such as the weight of sand being hauled in a truck, is measured in tons. There are short tons and long tons.
ton: a unit of weight (mass) in the imperial system (also called a short ton)
1 ton = 2000 lb
short ton: a unit of weight (mass) in the imperial system (also called a ton)
1 short ton = 2000 lb
long ton: a unit of weight (mass) in the imperial system
1 long ton = 2240 lb
Did You Know?
The British defined the ton as equal to 160 stone when they considered the stone as the basic unit of weight. One stone equals 14 lb. Therefore, the British ton, now also known as the long ton, is equal to 2240 lb.
Since 1 kg is about 2.2 lb, what would an approximation of the metric tonne be in pounds? Do you agree that
1 tonne =![]()
Which is a metric tonne closer to—a short ton or a long ton? Since 1 tonne is almost 2200 lb, 1 metric tonne and 1 long ton are almost the same!
Study these examples to see how to apply the definitions of tons.
Example 3
Mr. Watnee hauls gravel. He estimates that 1 yd3 weighs 3000 lb. How many tons (short) would a 5-yd3 load of gravel weigh?
Solution
So,
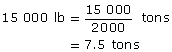
Mr. Watnee’s load of gravel weighs 7.5 tons.
 Self-Check
Self-Check
Do the following questions.
SC 5. Sergey loaded 200 bushels of wheat into the box of his truck. The grain weighed 5.2 tons (short). How many pounds did each bushel of wheat weigh?
SC 6. If 1 yd3 of gravel weighs 1.5 tons, how many pounds does 1 ft3 of gravel weigh? Round your answer to the nearest pound.
Mass Conversions
As for length, area, volume, and capacity, there is a need, from time-to-time, to convert masses (weights) between the imperial and SI systems. Remember that the pound was defined in terms of the kilogram. One pound is defined as exactly 0.453 592 37 kg.
So, you can set up tables to convert between systems. First work through the following example.
Example 4
How many grams are there in 1 oz?
Solution
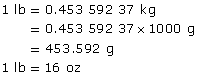
So,
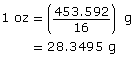
There are approximately 28 g in 1 oz.
 Self-Check
Self-Check
Now you will complete a set of tables for converting among imperial and SI units.
Do the following questions.
SC 7. Complete the following table by filling in the missing entries. Round to 4 decimal places.
|
Imperial |
Metric |
|
1 oz |
28.3495 g |
|
1 lb |
0.4536 kg |
|
1 ton (short) = 2000 lb |
__________ t |
|
1 ton (long) = 2240 lb |
__________ t |
SC 8. Complete the following table by filling in the missing entries. Round to 4 decimal places.
|
Metric |
Imperial |
|
1 g |
__________ oz |
|
1 kg |
__________ lb |
|
1 t |
__________ ton (short) |
|
1 t |
__________ ton (long) |
Now you can use the tables from SC 7 and SC 8 to convert weights and masses! Study these examples. You may wish to do the questions first and then compare your answers to the given solutions.
Example 5

BananaStock/Thinkstock
Gabi weighs 116 lb. What is her mass to the nearest kilogram?
Solution
![]()
So,
![]()
Gabi’s mass is about 53 kg (to the nearest kg).
Now check your skills in converting between imperial weights and SI masses.
You may also use the multimedia “Imperial to SI Weight Conversion” to confirm your calculations for the questions that follow.
 Self-Check
Self-Check
Do the following questions.
SC 9. Apples cost $0.79 per pound. What is their cost per kilogram? Round your answer to the nearest cent.
SC 10. The mass of a Canadian two-dollar coin is 7.3 g. What is its weight in ounces?
SC 11. How much does 1 gal of water weigh in pounds if 1 L of water has a mass of 1 kg? Round your answer to the nearest pound.
 Mastering Concepts
Mastering Concepts
Try this question. You will apply your knowledge from a previous lesson about volume and capacity.
Connie is planning to lay a concrete driveway 60 ft long, 15 ft wide, and 4 in thick. If 1 yd3 of concrete weighs 4000 lb, how many tons of concrete are needed for the driveway? Round your answer to 1 decimal place.
1.20. Page 5
Module 2: The Imperial System
Lesson Summary

© Inga Nielsen/shutterstock
When following a recipe, do you feel more comfortable measuring weights and volumes in the SI or imperial system?
In this lesson you explored the following lesson questions:
- How are weights (masses) commonly measured in the imperial system?
- What is the history of units for mass in the imperial system?
- How are the units for weight in the imperial system related?
- How are the units for weights in the imperial system applied in practical situations?
- How are masses (weight) converted between the imperial and SI units?
Check your level of understanding of the materials covered in this lesson by completing “Lesson 4 Traffic Lights.” If you select an amber or red traffic light in the multimedia piece, you will receive information about additional work you can complete to improve your understanding of the topics. Complete the suggested work before you proceed to the Lesson 4 Assignment. If you experience difficulty, contact your teacher before starting the Lesson 4 Assignment.
You discovered that the common units for weight in the imperial system are the pound, ounce, and the short and long tons. You explored converting weight to mass in the metric system. You will remember that one pound is a little less than one-half kilogram.
 Assignment
Assignment
Retrieve the Lesson 4 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment. Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Unit Project
Before you move on to the next lesson, you should be close to completing the second part of the Unit 1 Project. Contact your teacher to report your progress and to seek advice.
1.21. Lesson 5
Module 2: The Imperial System
Lesson 5: Temperature
Focus

© Pixelite/shutterstock
Have you thought about how temperatures might affect your Unit Project design? Designing habitats for people and animals must take climate into account!
When holidaying in Canada or the United States, national parks are always a favourite destination for seeing the natural beauty of the country.
Joshua Tree National Park is located in the desert of southern California. This park is renowned for its spectacular rock formations and unusual vegetation. The desert climate is one of extremes. In January the daytime temperatures can be warm enough for short sleeves and shorts, but at night the temperature can dip well below freezing.
If you have travelled in the United States, you know they do not use the Celsius thermometer. Americans measure temperature in degrees Fahrenheit.
In this lesson you will explore the following questions:
- How are temperatures measured on the Fahrenheit scale?
- With what common Fahrenheit temperatures should you be familiar?
- How are the Celsius and Fahrenheit scales related?
- How can temperatures on one scale be converted to the other?
Assessment
You will complete the Lesson 5 Assignment Booklet for assessment. Download the Lesson 5 Assignment Booklet save it in your course folder now.

© cen/shutterstock
You will receive further instructions on how to complete the Assignment Booklet later in this lesson. You will also be prompted to start working on the Unit 1 Project.
Remember to save all activities, including those that are not part of the Assignment, in your course folder.
Required Materials and Equipment
You will need a thermometer that has both a Celsius and Fahrenheit scale—like the one in the photograph. Alternately, you may use the Simulated Thermometer to perform the activities. You will also need a calculator.
1.22. Page 2
Module 2: The Imperial System
Get Started
In this activity you will explore some of the steps used to develop important points on the Fahrenheit scale.
You will need a thermometer with both Celsius and Fahrenheit scales, ice, water, and table salt; or you may use the multimedia tool “Simulated Thermometer” to complete the activity.
 Try This
Try This
TT 1. Work with a partner if possible. Use the multimedia tool or a real thermometer to record the temperatures in Celsius and Fahrenheit for these three different situations. Discuss and record your observations.
|
Situation |
Temperature on the Celsius (°C) Scale |
Temperature on the Fahrenheit (°F) Scale |
Observations About the Two Temperature Scale Readings |
|
Freezing/Melting Point of Water cup of water full of ice (Record the temperature when half the ice is melted.) |
|
|
|
|
Ice/Salt Mixture crushed ice with a handful of salt (Record the temperature once the ice has started to melt.) |
|
|
|
|
Body Temperature armpit (Record the temperature after three minutes.) |
|
|
n/a |
 Share
Share
It’s time to share your answers to TT 1. Remember that sharing work is an important part of learning. Use the following tips to ensure you get all the benefits from this sharing opportunity:
- Complete the questions to the best of your ability. Make sure your answers are in a form that you can easily share with another student or with your teacher, if so directed.
- Use your class discussion area, or another method indicated by your teacher, to post your answers and to view the work of the people you’re sharing with.
- Compare your answers to the other posted answers. Identify where you have similar answers and where your answers are different. Discuss all differences between answers until you agree on the answers. If necessary, you may wish to involve your teacher in your discussion.
- Revise your answers where necessary.
Save a revised copy of your work in your course folder. Ask your teacher whether you should also save a summary of your discussion in your course folder.
Now that you are familiar with some benchmarks on the Fahrenheit and Celsius scales, you should be prepared to complete the activities in Explore.
1.23. Page 3
Module 2: The Imperial System
Explore
Work with a partner if possible.
In Module 1 you explored the Celsius scale. Do you remember the freezing point of water in degrees Celsius? In your activity in Get Started, you discovered that the freezing point of water on the Fahrenheit scale is 32°F and that this temperature corresponds to 0°C.
Recall that the boiling point of water is 100°C. In degrees Fahrenheit, water boils at 212°F.
 Try This
Try This
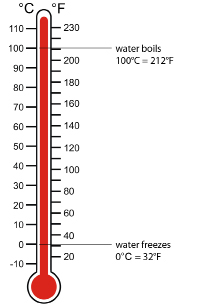
© Ivanou Aliaksandr/shutterstock
Use this thermometer to answer the Try This questions.
Use information from the graphic of the thermometer to help you answer the following questions.
TT 2. How many Celsius degrees are there between freezing and boiling?
TT 3. How many Fahrenheit degrees are there between freezing and boiling?
TT 4. Which degree is larger—a Fahrenheit degree or a Celsius degree? How do you know?
Do you need a quick review on expressing fractions in their simplest terms to help you answer TT 4? To express a fraction such as ![]() in its simplest terms, divide 10 and 18 by their largest possible whole number factor.
in its simplest terms, divide 10 and 18 by their largest possible whole number factor.
TT 5. Determine each of the following ratios. Express them as fractions in their simplest terms.
Use your answers for the ratios in a. and b. to complete these equations by writing in the appropriate fractions.
- 1 Celsius degree = __ × 1 Fahrenheit degree
- 1 Fahrenheit degree = __ × 1 Celsius degree
TT 6. How might these fractions be used to help work between these two temperature systems? You may use an example from the chart in Get Started. Note that, later in the lesson, you will be asked to attach a copy of your response to TT 6 to your Assignment Booklet. Your response to TT6 will be marked as part of your Assignment Booklet.
 Share
Share
It’s time to share your answers from TT 2 to TT 6. Remember that sharing work is an important part of learning. Use the following tips to ensure you get all the benefits from this sharing opportunity.
- Complete the questions to the best of your ability. Make sure your answers are in a form that you can easily share with another student or with your teacher, if so directed.
- Use your class discussion area, or another method indicated by your teacher, to post your answers and to view the work of the people you’re sharing with.
- Compare your answers to the other posted answers. Identify where you have similar answers and where your answers are different. Discuss all differences between answers until you agree on the answers. If necessary, you may wish to involve your teacher in your discussion.
- Revise your answers where necessary.
Save a revised copy of your work in your course folder. Ask your teacher whether you should also save a summary of your discussion in your course folder.
The largest whole number that divides both 10 and 18 is 2.
So,
![]()
1.24. Page 4
Module 2: The Imperial System
Bringing Ideas Together
Now you will bring the ideas from Get Started and Explore together to examine the Fahrenheit scale more closely.
The Fahrenheit Scale
The Fahrenheit scale was devised by Daniel Fahrenheit almost 300 years ago. Fahrenheit was a German instrument maker and scientist. He worked with a scientist in Denmark. Fahrenheit proposed that 0° on his scale would be the temperature of a mixture of ice, water, and certain salt. Fahrenheit used ammonium chloride rather than table salt. He thought the temperature of this mixture was the coldest temperature possible in Denmark.
Did you get a similar temperature for your mixture of ice, water, and table salt in Get Started?
Fahrenheit used body temperature as the next benchmark. He called that temperature 96°. He chose 96 instead of 100 because 96 could be divided by 12 just like the number of inches in a foot. Based on these benchmarks, the freezing point of water on this scale was 32°.
When his scale was revised, it was decided to keep 32° as the freezing point of water and make 212° the boiling point so there would be an even 180° between them! It is interesting that after this small adjustment, body temperature was not 96° as Fahrenheit wanted, but 98.6°.
The Fahrenheit temperature scale is a scale that sets the freezing point of water at 32°F and the boiling point of water at 212°F.
 Try This
Try This
In this activity you will establish more benchmarks on the Fahrenheit scale. You will use these benchmarks to become bilingual in Celsius and Fahrenheit!
TT 7. Use the Internet or other sources of information, including people you know, to complete the following chart.
|
Description |
Degrees Fahrenheit |
Degrees Celsius |
|
normal body temperature |
|
|
|
warm summer day |
|
|
|
room temperature |
|
|
|
pleasant spring day |
|
|
|
water freezes |
|
|
|
time to plug in the car |
|
|
 Share
Share
It’s time to share your answers to TT 7. Remember that sharing work is an important part of learning. Use the following tips to ensure you get all the benefits from this sharing opportunity.
- Complete the questions to the best of your ability. Make sure your answers are in a form that you can easily share with another student or with your teacher, if so directed.
- Use your class discussion area, or another method indicated by your teacher, to post your answers and to view the work of the people you’re sharing with.
- Compare your answers to the other posted answers. Identify where you have similar answers and where your answers are different. Discuss all differences between answers until you agree on the answers. If necessary, you may wish to involve your teacher in your discussion.
- Revise your answers where necessary.
Save a revised copy of your work in your course folder. Ask your teacher whether you should also save a summary of your discussion in your course folder.
Now with these benchmarks and your work in Explore, you are ready to convert between Celsius and Fahrenheit. Study these examples.
Converting Between Temperature Scales
Example 1

Ryan McVay/Digital Vision/Thinkstock
Last night the temperature dropped to 15°C. What is this temperature in Fahrenheit?
Solution
15°C is 15 Celsius degrees above freezing.
The Celsius degree is larger than the Fahrenheit degree.
There are 9 Fahrenheit degrees for every 5 Celsius degrees.
So, the number of Fahrenheit degrees above freezing is ![]() times the number of Celsius degrees.
times the number of Celsius degrees.
There are ![]() Fahrenheit degrees above freezing.
Fahrenheit degrees above freezing.
But freezing is 32°F.
So,
![]()
Therefore, 15°C is 59°F.
You could have done this problem in one step using the formulas learned in TT 6.
The formula is
Fahrenheit temperature = ![]() × Celsius temperature + 32
× Celsius temperature + 32
Note: This formula can be used regardless of whether the temperature is plus or minus!
This formula can be abbreviated as follows: ![]() .
.
So,
![]()
The temperature in Fahrenheit is 59°F.
Example 2
Use the formula to convert –7°C to Fahrenheit.
Solution
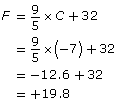
So, –7°C is 19.8°F.
Now, how would you convert Fahrenheit to Celsius?

© Lai Leng Yiap/15793094/Fotolia
Example 3
Convert 68°F to Celsius.
Solution
Celsius is the number of degrees above or below freezing.
Freezing is 32°F.
So, 68°F is 68 - 32 = 36 Fahrenheit degrees above freezing.
Remember, there are only 5 Celsius degrees for every 9 Fahrenheit degrees.
Multiply the number of Fahrenheit degrees by ![]() .
.
number of Celsius degrees above freezing ![]()
Therefore, 68°F = 20°C.
You could have done this problem in fewer steps.
Celsius temperature ![]() (Fahrenheit temperature –32)
(Fahrenheit temperature –32)
Note: This formula, just like the other, can be used regardless of whether the temperature is above or below zero!
This formula can be abbreviated ![]() .
.
So,
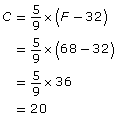
Therefore, 68°F = 20°C.
Example 4
The temperature last January in Minot, North Dakota, fell to –30°F. What was this temperature to the nearest tenth in degrees Celsius?
Solution
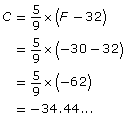
So, –30°F is approximately –34.4°C.
Use the interactive Temperature Conversion to confirm the solution to the previous example.
 Self-Check
Self-Check
You will now apply, in everyday settings, the formulas for converting between temperature scales.
Do the following questions and check your answers using the interactive “Temperature Conversion” that you accessed in Example 4.
SC 1. Martin has a fever of 101.3°F. How many Fahrenheit degrees above normal is his temperature?
SC 2. The coldest temperature in Canada was –63°C recorded on February 3, 1947, in Snag, Yukon. What is this temperature in Fahrenheit?

iStockphoto/Thinkstock
SC 3. The highest recorded temperature in Death Valley in the southwestern United States was 134°F reached on July 10, 1913. What is this temperature in Celsius? Round your answer to 1 decimal place.
SC 4. A recipe for Swiss steak calls for an oven temperature of 160°C. What would the oven setting be in Fahrenheit?
Oven Temperature Readings
Temperatures on the dials of older ovens in Canada and most ovens in the United States are in degrees Fahrenheit. SC 4 is interesting because 320, the oven temperature in Fahrenheit, is exactly two times 160, the equivalent oven temperature in Celsius.
320 = 2×160
This relationship can be used to convert between Celsius and Fahrenheit cooking temperatures. Even though for all temperatures other than 160°C this technique is just an approximation, it is close enough in the kitchen!
Example 5
A recipe for cookies calls for an oven temperature of 400°F. What is the approximate oven temperature in Celsius?
Solution
The Fahrenheit temperature is roughly twice the Celsius temperature.
400 = 2×200
So, 400°F is about 200°C.
 Self-Check
Self-Check
Do the following questions.
SC 5. A recipe for lasagna calls for an oven temperature of 175°C. What is the approximate Fahrenheit temperature?
SC 6. The directions on a package of frozen French fries states “Preheat oven to 450°F.” What would be the metric equivalent?
 Mastering Concepts
Mastering Concepts
If you have mastered the concepts in this lesson and would like a challenge, try these questions.
MC 1. Scientists state that the temperature at which molecular motion is at a minimum is approximately –273.15°C. What is the equivalent temperature in degrees Fahrenheit?
MC 2. Zero on the Rankine scale correlates to the Celsius temperature at which the molecular motion is at a minimum. Each degree on the Rankine scale is the same size as the degree on the Fahrenheit scale. What would body temperature be on the Rankine scale?
MC 3. On the Kelvin scale, the temperature at which molecular motion is at a minimum is set to be 0 K. Each degree on the Kelvin scale is the same size as the degree on the Celsius scale. Approximately what would body temperature be on the Kelvin scale?
1.25. Page 5
Module 2: The Imperial System

© ALPO/shutterstock
Lesson Summary
Winter and summer sports are governed by the weather. Do you check weather forecasts when planning your weekend activities? In Canada since the 1960s, temperature is reported on the Celsius scale, but if you were in the United States today, the temperature would be given in Fahrenheit.
In this lesson you explored the following lesson questions:
- How are temperatures measured on the Fahrenheit scale?
- With what common Fahrenheit temperatures should you be familiar?
- How are the Celsius and Fahrenheit scales related?
- How can temperatures on one scale be converted to the other?
Check your level of understanding of the materials covered in this lesson by completing “Lesson 5 Traffic Lights.” If you select an amber or red traffic light in the multimedia piece, you will receive information about additional work you can complete to improve your understanding of the topics. Complete the suggested work before you proceed to the Lesson 5 Assignment. If you experience difficulty, contact your teacher before starting the Lesson 5 Assignment.
To answer these questions, you investigated the way temperatures are measured in Celsius and Fahrenheit. You looked at some common Fahrenheit and Celsius temperatures.
You then explored the relationship between Celsius and Fahrenheit and how a temperature can be converted between the two scales.
 Assignment
Assignment
Retrieve the Lesson 5 Assignment Booklet you saved in your course folder at the start of this lesson. Complete the Assignment Booklet. Resave your Assignment Booklet in your course folder and submit a copy to your teacher for assessment.
Now you should have all the skills needed to complete your Unit 1 Project. Contact your teacher to report your progress and to seek advice.
1.26. Module 2 Summary
Module 2: The Imperial System
Module 2 Summary

© Marek Slusarczyk/shutterstock
If you have travelled to the United States, you know that the U.S. still uses a modified form of the imperial system. There, gasoline is sold in gallons, milk in quarts, sugar and flour in pounds, and lumber in feet and inches. Road signs are in miles and speed limits are in miles per hour. Temperature forecasts are in Fahrenheit. Travelling in the United States or shipping goods across the border means you need a basic knowledge of the American units for weights and measures.
In this module you used these units for weights and measures when you explored the following questions:
- What is the imperial system of weights and measures and how is it used to measure length, area, volume, capacity, weight, and temperature?
- What are the relationships among metric units, imperial units, and American customary units?
A picture can tell a story. The Module 2 Lessons Summary is a collection of images from each lesson that describes the math you explored. What do you remember about each image? Can you relate each image to something new you learned in this module ? Watch “Module 2 Lessons Summary” now.