Lesson 10: Solving Right Triangles and Word Problems
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 10: Solving Right Triangles and Word Problems |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 3:27 AM |
Description
Created by IMSreader
Focus
Module 1: Measurement and Its Applications
Lesson 10: Solving Right Triangles and Word Problems
** Always have your calculator in degree mode. Check by hitting the MODE button and looking at the third line. The word degree must be darkened**
Focus

© psamtik/shutterstock
You may enjoy listening to music. The music may have been recorded digitally—a process that uses trigonometry. Perhaps the music is in MP3 format using data compression, which uses an understanding of the human ear’s ability to distinguish between sounds, and this format also requires trigonometry.
You may travel over a bridge today. That bridge was built using an understanding of forces acting at different angles. You will notice that bridges involve many triangles—trigonometry was used when designing the lengths and strengths of those triangles.
You will often see a surveyor at work in your community. Trigonometry helps the surveyor determine sides of a triangle that are difficult to access. An angle that cannot be reached may be measured from places that can be reached.
Earlier in the module, you saw an example of this principle when you read about building a tree house. The heights of trees and tall buildings can be determined by knowing the distance to the base of the tree or building. Similarly, distances across rivers or busy roads can be determined by using angle and length measurements from one side of the river or the road.
In the last two lessons you used the trigonometric ratios to find sides and angles in right triangles. In this lesson you will apply those skills to solve triangles ( finding all missing angles and sides) as well as solve real world problems.
Outcomes
At the end of this lesson, you will be able to
- solve a right triangle ( find all missing sides and angles)
- solve a problem that involves right triangles
- solve a problem that involves one or more right triangles by applying the primary trigonometric ratios or the Pythagorean theorem
- solve a problem that involves indirect measurement using the trigonometric ratios, the Pythagorean theorem, and measurement instruments such as a clinometer or a metre-stick
Lesson Questions
-
How do you approach problems whose solutions are based on trigonometry and its principles?
-
How is trigonometry used to determine heights and distances that cannot be directly measured?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Assess tab or by using the Quizzes link under the Activities block.
** Note – Share questions may have to be done on your own depending on your learning situation**
Launch
Module 1: Measurement and Its Applications
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
1. Find the unknown length. Show your answers rounded to the nearest tenth of a metre.
a. 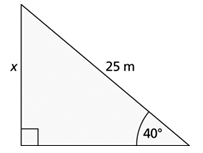
b. 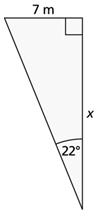
2. Find the unknown angle. Show your answers rounded to the nearest degree.
a. 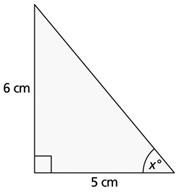
b. 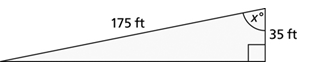
3. For each of the triangles in question 2, use the Pythagorean theorem to calculate the length of the third side. Show your answers rounded to the nearest tenth.
4. What is the difference when two shapes are said to be similar compared to when two shapes are said to be congruent?
5. The following two triangles are similar.
a. What is the measure of angle B in Triangle 2?
b. Calculate the length of c in Triangle 1. (Hint: If you do not have enough information for the Pythagorean theorem, you could use proportions.)
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
![]() Refresher
Refresher
In this lesson you will be using the trigonometric ratios and the Pythagorean theorem to solve problems you encounter in your everyday life. These problems will all involve right angle triangles. Do you remember what makes a triangle a right angle triangle?
“Space and Shape: Trigonometry” provides a good review before you begin problem solving. On the right-hand side of the website, click on “Interactive.” When you are finished, choose “Video.”
The video at “Space and Shape: Similarity and Congruence” shows the difference between similar and congruent shapes. For example, are stop signs congruent or similar to other stop signs? View the video to find out. On the right-hand side of the website, choose “Video.”
Once you have viewed the video, choose “Interactive.” Viewing the interactive information is a fantastic way to figure out if you are truly comfortable with congruent and similar shapes. The site allows you to move and reshape triangles to determine if they are congruent, similar, or neither when compared to each other.
Please review your work from Lesson 7 for the definition of the trigonometric ratios. You will also need to solve triangles in which two pieces of information are given and you have to find either a length or an angle. Remember the six types of solving triangles from Lesson 7.
Materials
- tape measure
- clear plastic ruler
- clear plastic protractor
- clear tape
- cotton string
- small weight (e.g., a metal washer)
You will also need the following items to complete Math Lab: Clinometer.
- 1 plastic protractor
- 1 soda straw
- 1 paper clip
- 1 toothpick or another paper clip
- 1 6–8 in (15–20 cm) length of thread
- 1 roll of fishing line or relatively inflexible string (The length depends upon use.)
- 2 pieces of tape (e.g., transparent, masking, duct)
Explore
Module 1: Measurement and Its Applications
Explore
Glossary Terms
Add these terms to your glossary:
- angle of depression
- angle of elevation
- clinometer
- congruent triangles
- similar triangles
---------------------------------------------------------------------------------------------------------------------
Solving Right Triangles
 Read
Read
Find out how to solve a triangle when you are given different measures of a triangle. Read the textbook that you are using for this course.
Pay attention to the numbers that are used in each calculation. Every time a new measure is calculated, one more number can be used to determine the next unknown measure.
What reasons are there for using the original given measures? What reasons are there for using calculated measures?
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Solving a Right Triangle Given Two Sides” on pages 106 and 107 to see two methods for solving a right triangle given two sides.
Read “Example 2: Solving a Right Triangle Given One Side and One Acute Angle” on page 108 to see how to solve a right triangle given the measure of one length and one acute angle.
 Watch and Listen
Watch and Listen
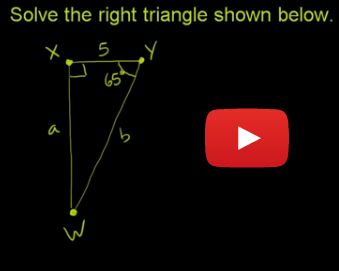
Watch the following Khan Academy Video to get a better understanding of what it means to Solve a Right Triangle.
 Try This 1
Try This 1
Use what you have learned in this lesson to solve some triangles. Remember to use a calculated value to solve for another value only if you are sure of the correctness of the calculated value. If the calculated value is incorrect, then the subsequent values will also be incorrect.
Complete the following in your course folder ( binder).
Foundations and Pre-calculus Mathematics 10 (Pearson), question 6 on page 111.
Use the link below to check your answers to Try This 1.
Possible TT1 (Try This 1) Solutions
---------------------------------------------------------------------------------------------------------------------
Solving Word Problems
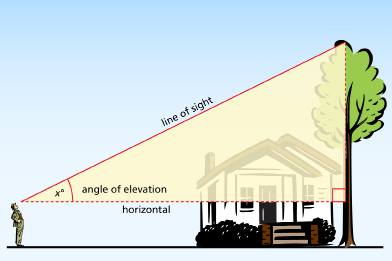
man, house, tree: Image Club ArtRoom/Getty Images
Sometimes you will see either the expression angle of elevation or angle of depression when you are solving a word problem involving angles.
The angle of elevation is the angle from the horizontal to the line of sight as shown in the diagram.
The angle of elevation is useful to know in problems where the observer is looking upwards at something.
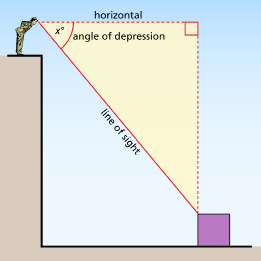
man: Image Club ArtRoom/Getty Images
The angle of depression, on the other hand, refers to those instances when the observer is looking downwards at something. Like the angle of elevation, the angle of depression is the angle between the horizontal and the line of sight. The difference is that the line of sight, in this case, is directed downwards. **IMPORTANT** Do NOT put the angle of depression between the vertical and then line of sight. This is a COMMON error.
![]() Try This 2
Try This 2
What is the relationship between the angle of elevation and the angle of depression? Try the following exercise to see if you can discover what the relationship is.
Read the following scenario and complete the following in your course folder ( binder)
Romeo is standing in Juliet’s yard. Juliet, meanwhile, is standing on her balcony three stories above the ground. Each one is looking at the other person.
Step 1. Sketch a simple diagram showing this scenario. Place a copy of your sketch in your course folder.
Step 2. In your sketch, use a ruler to draw Romeo’s line of sight to Juliet.
Step 3. Show the angle of elevation from the horizontal to his line of sight. Add it to your sketch.
Step 4. In your sketch, show the angle of depression from the horizontal to Juliet’s line of sight. (Hint: Juliet’s line of sight is the same as Romeo’s.)
Step 5. Use a protractor to measure the angle of elevation and the angle of depression. What do you notice?
Use the link below to check your answers to Try This 2.
Explore 2
Module 1: Measurement and Its Applications
 Did You Know?
Did You Know?
Trigonometry is used in the fields of design, music, navigation, cartography, manufacturing, physics, optics, projectile motion, and other disciplines that involve angles, fields, waves, harmonics, and vectors.
Trigonometry problems vary in complexity. Some problems involve only one right triangle and one or two steps. Other problems may involve two triangles and may require several calculations. You can approach these problems by following these guidelines:
- Sketch the scenario: Set up the problem with a drawing.
- Find the right triangle(s): You will need to identify the triangle or triangles in your sketch. Label the given lengths and/or angles. Also, label the length or the angle that you need to find.
- Write a trigonometric equation: Use SOH CAH TOA and the information given in the problem to select an equation—sine, cosine, or tangent—to solve.
- Solve the equation: Rearrange the equation, and solve for the unknown length or angle.
 Math Lab: Creating a Clinometer
Math Lab: Creating a Clinometer
Print the document Math Lab: Creating a Clinometer (or copy by hand) and complete the excercises. Some of this will be included in your Module Assignment.
Math Lab Analysis Answers
Example
Retrieve your data from Math Lab: Creating a Clinometer that you saved to your course folder ( binder). This example will take you through the steps that were just outlined to help you determine the height of the structure you measured.
One of the required measurements from the Math Lab is the angle of elevation from the horizontal to the top of the structure that you measured. Read the Caution bubble to see how to make sure you read the information correctly.
 Caution
Caution
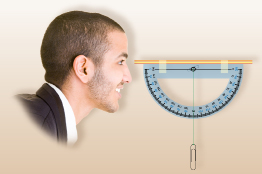
man: © Robert Kneschke/shutterstock
Figure 1
When the clinometer is held parallel to the ground along the horizontal, the string passes through 90° (see Figure 1).
Suppose that when the clinometer is tilted to view the top of the tree, the string now passes through 120° (see Figure 2).

man: © Robert Kneschke/shutterstock
Figure 2
The reading that should be reported is 120° − 90° = 30°.
This is because the clinometer started at 90° and then rotated through 30° to reach 120°.
If you recorded 120° as the angle of elevation, it means that you started at the horizontal and rotated your line of sight 120° upwards. Since a 90° rotation would mean you would be looking straight up, 120° would mean you are now looking slightly behind you.
For this example, assume that the measurements taken were the following:
- The distance between you and the base of the tree is 10 m.
- The string on the clinometer passes through 140°.
- The distance from the ground to the eye level of the person taking the measurement is 1.5 m.
Follow the steps to solve for the height of the tree.
Sketch the Scenario
The angle of elevation is 140° − 90° or 50°.
A sketch might look like the following.
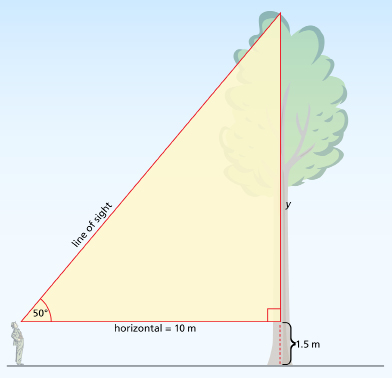
man, tree: Image Club ArtRoom/Getty Images
Find the Right Triangle(s)
The right triangle is coloured red. The distance between you and the tree is 10 m. The angle of elevation is 50°.
The length that needs to be found is y.
Write a Trigonometric Equation
Using 50° as the reference angle, the known side is the adjacent side, and the required side is the opposite side.
The ratio that contains both of these sides is tangent (TOA). So the equation is
![]()
Solve the Equation
Multiplying both sides of the equation by 10 gives the following:
![]()
Don’t forget to add the height to eye-level!
The height of the tree is 11.9 m + 1.5 m = 13.4 m.
 Try This 3
Try This 3
Apply the steps shown in the example to your own measurements to obtain the height of the structure you selected in Math Lab: Constructing a Clinometer.
Be sure to include the following:
- A description of the structure you chose.
- All of your measurements.
- All of your calculations, including sketches.
- A final answer along with an assessment of how reasonable it is.
Save your work as you will hand it in as part of your Module 1 Part 2 Assignment.
 Read
Read
You now have an idea of the approach you can take with trigonometry problems. Read the following examples to see how you can apply this same approach given different circumstances. Read the textbook that you are using for this course.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 3: Solving an Indirect Measurement Problem” on page 100 to see how to approach a similar problem where a measurement is made indirectly. Why can’t you use tangent to solve this problem?
Explore 3
Module 1: Measurement and Its Applications
 Try This 4
Try This 4
Complete the following in your course folder ( binder).
Foundations and Pre-calculus Mathematics 10 (Pearson).
TT 4. Complete “Exercises” questions 6, 7, and 11 on pages 101 and 102.
Use the link below to check your answers to Try This 4.
Possible TT4 (Try This 4) Solutions
 Self-Check
Self-Check
Choose the correct answer.
SC 1. In a triangle, the sum of all angles equals ________.
A. 180°B. 90°
C. 360°
D. There is not enough information given to answer this question.
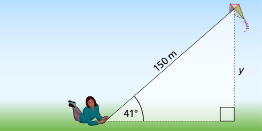
SC 2. A kite has a string 150-m long. If the string makes an angle of 41° with the ground, find the height of the kite above the ground.
A. 98 m
B. 113 m
C. 150 m
D. 168 m
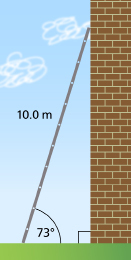
SC 3. A 10.0-m ladder leans against a vertical wall. The angle between the ladder and the ground is 73°. Find the distance from the foot of the ladder to the wall.
A. 2.9 m
B. 7.6 m
C. 9.6 m
D. 15.9 m
woman © Volume 43 Everyday Woman/Getty Images
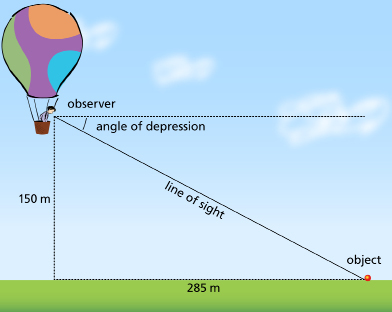
SC 4. A person in a hot air balloon is 150 m above the ground. An object is 285 m away from the balloon on a line directly beneath the balloon. What is the angle of depression of the person’s line of sight to the object on the ground rounded to the nearest degree?
A. 28°
B. 32°
C. 62°
D. 58°
 Caution
Caution
It is important to realize that the same angle can be produced from many different triangles. You should observe that, although the side lengths that make up the triangle may vary, the value of a ratio, such as sin 30°, does not vary.
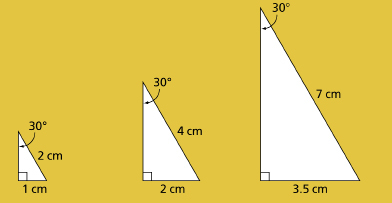
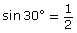
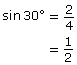
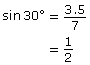
Some trigonometry problems need to be modelled with two triangles. For this type of problem, you will need to determine the measure of either a length or an angle from each triangle. You may need to calculate the measure of a length or angle on one triangle before you can determine the length on another triangle.
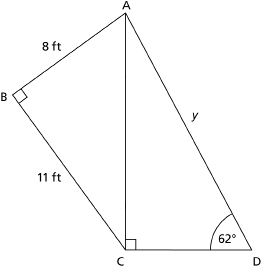
Example
In the diagram, the given distances are as follows:
AB = 8 ft
BC = 11 ft
CD = 9 ft
What is the distance from point A to point D?
Solution
The length AD is labelled y in triangle ACD. There is not enough information to solve triangle ACD. You would need to know the length of another side in triangle ACD in order to solve the triangle. However, there is enough information to solve triangle ABC.
Notice that triangles ACD and ABC have length AC in common. You can solve triangle ABC for length AC. Once you know the length of AC, you will have enough information to solve for all unknown measures of triangle ACD, including length AD.
In triangle ABC,
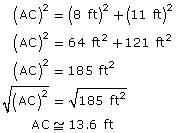
In triangle ACD, you now know the length of the side opposite 62°, and you are solving for the hypotenuse y.
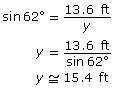
 Read
Read
Read the textbook that you are using for this course. Read through the following additional example to see how a trigonometry problem can be modelled by two right triangles. Pay attention to the extra step at the end. Why is this step necessary?
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 2: Solving a Problem with Triangles in the Same Plane” on pages 115 and 116, which demonstrates how to solve a two-triangle trigonometry problem involving the height of a building.
 Try This 5
Try This 5
Remember as you model and solve problems involving two triangles that you can only solve a triangle if you have enough information. If you don’t have enough information in one triangle, then you need to solve the other triangle to get the values you need for the first triangle.
Complete the following in your course folder ( binder).
Foundations and Pre-calculus Mathematics 10 (Pearson).
TT 5. Complete “Exercises” questions 3.b), 9, and 11 on pages 118 and 119.
Use the link below to check your answers to Try This 4.
Possible TT5 (Try This 5) SolutionsConnect
Module 1: Measurement and Its Applications
You have seen that trigonometry can be used to model real-world problems. In fact, the concepts of trigonometry are applicable in the design of new homes, in the reconstruction of traffic accidents, in the use of navigation, and in other areas.
 Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Assess tab or by using the Quizzes link under the Activities block. Also ensure your work in your binder (course folder) is complete.
 Project Connection: The Staircase ** NOT ASSIGNED**
Project Connection: The Staircase ** NOT ASSIGNED**
It is time for you to do another common problem. Of course, it is still a collaborative approach—you can still work together with a partner. Go to the Unit 1 Project and complete the Lesson 8 portion of the project.
 Going Beyond
Going Beyond

handheld GPS: © Olaru Radian-Alexandru/shutterstock; GPS illustration: © Scott Maxwell/LuMaxArt/shutterstock
Did you know that trigonometry is the main math tool behind the technology of GPS (global positioning system)? Your car or your phone may have built-in GPS, so you never need to be lost! So how does GPS work?
GPS measures the satellite signals closest to your location by receiving signals from a minimum of three satellites, which is referred to as triangulation.
GPS locks onto a position and uses trigonometry to calculate its position. This position is measured in latitude and longitude. From that point, as long as the satellite stays locked onto your location, then GPS can provide the speed, the distance, and, most important of all, a map to your destination. Initiate an Internet search for GPS for a much more detailed explanation.
The trigonometry used in GPS systems does go beyond what you have learned in this course. An Internet search for GPS and spherical trigonometry can help you learn more.
Summary
Module 1: Measurement and Its Applications
Lesson 10 Summary
In this lesson you investigated the following questions:
-
How do you approach problems whose solutions are based on trigonometry and its principles?
-
How is trigonometry used to determine heights and distances that cannot be directly measured?
At the beginning of this lesson, you learned the steps for approaching problems based on trigonometry. You learned that the key first step is to sketch a diagram of the problem.
Then it is so important to correctly identify the right triangle in the problem and label the opposite, adjacent, and hypotenuse sides. You can then set up a sine, cosine, or tangent equation. This equation can then be solved to yield a solution.
In this lesson you also built a simple clinometer which helps you to measure heights which are otherwise difficult to measure directly. The height of a tree or a flagpole or your house can be measured from the safety of the ground. There is no need to climb the structure and drop down a measuring tape!
You have now completed the final lesson of Module 1 Part 2.