Lesson 3: Common Factors and Factoring Trinomials
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 3: Common Factors and Factoring Trinomials |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 5:23 AM |
Module 3: Polynomials
Lesson 3: Common Factors
Focus

both: Larrie Thomson/www.nightphotographer.com
Have you ever attended a live rock concert or any other live performance? If you have, you know that there is a lot of energy at those events. The sounds are amplified, and the visual effects on stage are spectacular.
In order for you to enjoy such a performance, many hours are dedicated to preparing for the event. Often, the stage is specially assembled for the show. Then, set pieces and music equipment are placed on the stage and many yards of cable are laid down. Fog machines and an assortment of lights are hung. Speakers are placed, and mics undergo sound checks. All of these pieces combine to produce a glamorous and visually stunning performance.
When the concert is over, the stage is disassembled and the individual pieces are packed up to be moved to the next venue.
Similarly, multiplying polynomials involves assembling smaller pieces into larger ones. In Lessons 1 and 2, for example, you learned how to multiply binomials to produce trinomials. Just as a stage can be disassembled, so too can polynomials be reduced to smaller pieces. In the remainder of this module you will learn how to break larger polynomials into smaller ones by factoring.
In this lesson you will learn strategies to factor various types of the polynomials called trinomials.
Outcomes
At the end of this lesson, you will be able to
- determine the common factors in the terms of a polynomial
- model the factoring of a trinomial of the form x2 + bx + c, concretely or pictorially, and record the process symbolically
- explain, using examples, the relationship between multiplication and the factoring of polynomials
- express a polynomial as a product of its factors
- factor a polynomial and verify by multiplying factors
Lesson Questions
- How are polynomial-factoring strategies similar to strategies used to obtain the prime factorization of a whole number?
- How can you tell if a polynomial is factored correctly?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Assess tab or by using the Quizzes link under the Activities block.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 3: Polynomials
Launch
Are you ready?
Complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
1. What does it mean to factor a number?
2. Determine the greatest common factor (GCF) of 60 and 72 by
a. listing the factors of each number
b. prime factorization
3. Multiply (3x + 2) and (x + 1) using
a. using algebra tiles
b. the area method
c. the distributive property
4.Verify your answer to question 3 by using the two-column method and substituting x = 3.
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
Answers
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources either before or after you try the Are You Ready? questions. Your teacher may also direct you to this section to review specific concepts.
You can review how to find the GCF of a set of number using a variety of strategies by looking at several examples in Module 2: Lesson1. Review “Find the GCF” to find out how to determine the GCF using prime factorization.
---------------------------------------------------------------
Watch the “Mathcast 007 Greatest Common Factor” . You only need to watch the first 3 minutes and 30 seconds of this clip. You can also review Module 2: Lesson1 to see some other methods for determining the GCF of a set of numbers.
-------------------------------------------------------------------
Watch the “Mathcast 005 Using an Area Model to Illustrate the Multiplication of a Binomial and a Binomial” . Watch the video to see how you can use algebra tiles to model the multiplication of binomials.
 Read
Read
You can read about how to verify the product of polynomial multiplication by reading an example of how to do this in your textbook.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Using the Distributive Property to Multiply Two Polynomials” on pages 183 and 184. Then read “Example 2: Multiplying Polynomials in More than One Variable” on page 184.
Materials
For this lesson, you may wish to use the set of algebra tiles that you borrowed from your teacher or that you created from the Algebra Tiles Template.
Alternatively, you could continue to use the “Arranging Algebra Tiles” applet.
Module 3: Polynomials
Discover
In Lesson1 you used algebra tiles to model the multiplication of two binomials. You then used algebra tiles to form the area of a rectangle. This area represented the product of the binomials. In this lesson you will work backwards beginning with by first forming a rectangular area.
 Math Lab: Exploring Factoring with Algebra Tiles
Math Lab: Exploring Factoring with Algebra Tiles
Print (or copy out by hand) and complete Math Lab: Exploring Factoring with Algebra Tiles.
Math Lab: Exploring Factoring with Algebra Tiles.
Use the link provided to check your work. *** DO the work before checking - this will lead to much better understanding**
Module 3: Polynomials
Explore

© bhowe/shutterstock
To factor a polynomial means to express it as a product. In the same way that a refrigerator cools food and a microwave oven warms food up again, multiplying polynomials and factoring are inverse operations. In other words, what can be done with one operation can be “undone” with the other operation. This concept is helpful when you are checking a solution. You can check the result of factoring by multiplying the factors. If the product is the same as the original polynomial, then you have factored correctly.
Just as there are multiple strategies for multiplying polynomials, there are also multiple strategies for factoring them. In this lesson you will investigate two strategies. The first one is applicable to all polynomials, and the second is a more specific one that applies to trinomials of the form x2 + bx + c.
Glossary Terms
Add these terms to your "Glossary Terms" in your notes:
- common factor
- factor
----------------------------------------------------------------
When you are required to factor a polynomial, the first task is to see if you can find a greatest common factor, or GCF. This is the first strategy you will investigate in this lesson.
In the Math Lab, you arranged tiles into rectangular areas. Did you notice that area of the rectangle is equal to the product of the dimensions? For example, to factor 2x + 4, you could take two x-tiles and four 1-tiles and arrange them as follows.
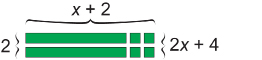
The dimensions of this rectangle are 2 by x + 2. As a result, you can express 2x + 4 as a product of its factors:
2x + 4 = 2(x + 2)
When you look at the factors, they cannot be broken down any further. In other words, x and 2 have no other common factors. Therefore, the binomial 2x + 4 has been completely factored.
 Caution
Caution
You may have also found that you can arrange the 2x + 4 tiles as a rectangle with dimensions 1 by 2x + 4.
![]()
While this is fulfilling the requirement of creating a rectangle from the available tiles, it is does not completely factor the polynomial. After all, 1(2x + 4) is still 2x + 4.
 Watch and Listen
Watch and Listen
Watch the video “Using the Area Model to Illustrate Common Factoring”.
An alternate way to factor a polynomial is to divide each term by the GCF.
Example
Factor the binomial 5x3 – 75x.
Step 1: Express each term in the polynomial as a product of its prime and variable factors.
![]()
Step 2: Identify the factors that both terms have in common; then multiply them together. Each term has a factor of 5 and x.
![]()
Step 3: Divide each term by the GCF and report the answer.
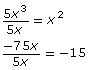
Therefore,
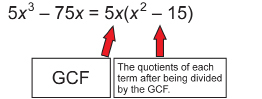
Step 4: Check your answer by using the distributive property to expand the expression.
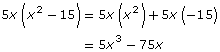
 Read
Read
Go to your textbook to reinforce the examples that have been shown. As you study the examples, try to find out when it would not be possible to factor a polynomial by arranging algebra tiles in the shape of a rectangle.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read pages 152 to 154. This includes the following:
- “Example 1: Using Algebra Tiles to Factor Binomials”
- “Example 2: Factoring Trinomials”
Next, read “Example 3: Factoring Polynomials in More than One Variable” on page 154.
 Tip
Tip
Whenever you need to factor a polynomial, the first thing you should do is to check whether the terms of the polynomial share a common factor. If so, you can use the GCF method to factor the polynomial. By doing so, you will be able to work with smaller numbers.
 Self-Check
Self-Check
SC 1. For each of the following polynomials, factor and state the GCF.
- 12x – 16
- 12x2y + 6xy2
- 4x3 + 2x2 – 6x
- –4x2y + 2xy
 Tip
Tip
When factoring by common factors, be sure that you factor the GCF out of all of the terms.
 Try This 1
Try This 1
Complete the following in your course folder ( binder). Show all work.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 1. Complete “Exercises” questions 4.a), 4.b), 8.a), 8.c), 10.b), 10.d), 10.f), 16.b), 16.d), 16.f), and 17 on pages 155 and 156.
Use the link below to check your answers to Try This 1.
Module 3 Polynomials
Part 2: Factoring Trinomials
There are many methods of factoring trinomials. How you decide which method to use will depend on the properties of the trinomial. In the remainder of this lesson you will focus on the methods used to factor trinomials of the form x2 + bx + c, where b and c are integers. NOTE: there is no number written in front of the squared term which indicates there is a 1 there.
Area Method
As you learned in the Math Lab, one way to factor trinomials is by using algebra tiles to form a rectangular area.
![]() Watch and Listen
Watch and Listen
Watch the video “Mathcast 010 Using the Area Model to Factor Trinomials” into a search engine. This videod shows you some more examples of how trinomials can be factored this way. Watch Example 1, it finishes at 3:31. (There are more examples done here - we will revisit this video in Lesson 4 to look at these).
![]() Self-Check
Self-Check
SC 2. Now that you have seen examples of how to use the area method to model the factoring of a trinomial, try the following Self-Check questions. Use algebra tiles or “Arranging Algebra Tiles” to factor each trinomial.
- x2 + 8x + 15
- x2 – x – 2
Product-Sum Method
Retrieve the Math Lab work from your course folder and review it. Examine your responses for “Analysis” questions 4.b. and 4.c. Did you notice a relationship between the numbers in the trinomial and the constants in the binomial dimensions?
Try the next activity to confirm your observations.
![]() Try This 2 - 4
Try This 2 - 4
Complete the following in your course folder ( binder).
TT 2. Complete the first four rows of the table.
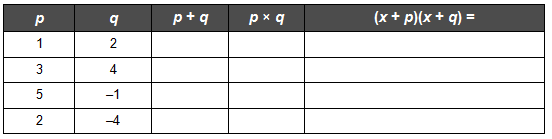
TT 3. Compare the numbers in the third column with the coefficients of the x-terms in the final column. What do you notice?
TT 4. Compare the numbers in the fourth column with the constants in the final column. What do you notice?
Use the link below to check your answers to Try This 2 - 4.
Possible TT2-4 (Try This 2-4) Solutions
The same result can be shown by a general expansion, where p and q represent any integer.

This expansion shows that the middle coefficient of the product of (x + p)(x + q) will always be the sum p + q, and the constant will be p × q.
------------------------------------------------------------------------------------------------------------------------------------------
This result leads to the product-sum method for factoring trinomials.
Do the following to factor a trinomial of the form x2 + bx + c using the product-sum method:
Step 1: Find two numbers whose product equals c and whose sum equals b.
Step 2: Write these numbers as the constant terms in two binomial factors, where each binomial has x as its first term.
---------------------------------------------------------------------------------------------------------------------------------------------------
Example 1 Factor x2 + 8x + 15.
Solution The first step is to find two numbers whose product equals c and whose sum equals b. Use a table to determine the integers whose product equals 15.
|
p |
q |
Product |
Sum |
|
1 |
15 |
15 |
16 |
|
3 |
5 |
15 |
8 |
Choose the combination that gives the correct sum. (In this example, the correct sum is shown in the second row of the chart.)
The next step is to express the polynomial as a product of its factors.
x2 + 8x + 15 = (x + 3)(x + 5)
![]() Read
Read
Go to your textbook to study further examples of factoring trinomials of the form x2 + bx + c. Pay careful attention to how factoring is accomplished when one or more terms in the trinomial is negative. What additional considerations are necessary when dealing with a negative product or a negative sum?
Foundations and Pre-calculus Mathematics 10 (Pearson)Read “Example 2: Factoring Trinomials” on page 163 and “Example 3: Factoring a Trinomial Written in Ascending Order” on page 164. |
![]() Watch and Listen
Watch and Listen
Watch this short recording that gives some help on how to be sure you have the entire set of factors when factoring a trinomial.
In some instances, you may have to apply more than one factoring technique before the trinomial is completely factored. Study the following example to learn how to approach this type of problem.
Example 2 Factor –3m2 – 12m + 36.
Verify by doing the following:
- multiplying the factors
- substituting m = 1
Solution Complete the following steps.
Step 1: Factor out the greatest common factor, where possible. Each term is divisible by –3.
–3m2 – 12m + 36 = –3(m2 + 4m – 12)
Step 2: Find two numbers, p and q, such that
- p × q = –12
- p + q = 4
Use a table to determine the integers whose product equals –12.
|
p |
q |
Product |
Sum |
|
1 |
–12 |
–12 |
–11 |
|
2 |
–6 |
–12 |
–4 |
|
3 |
–4 |
–12 |
–1 |
|
4 |
–3 |
–12 |
1 |
|
6 |
–2 |
–12 |
4 |
|
12 |
–1 |
–12 |
11 |
Choose the combination that gives the correct sum of 4. In this case, you will use the values in the fifth row.
Step 3: Express the polynomial as a product of its factors.
-3m2 - 12m+ 36 = -3( m2 + 4m - 12)
= -3 ( m + 6) ( m - 2)
Now you can verify. First, you can multiply the three factors in any order.

Since this result is the same as the original trinomial, the factors are correct.
Then, substitute m = 1 into the trinomial expression as well as the factor expression.
|
–3m2 – 12m + 36 |
3(m + 6)(m–2) |
|
|
|
|
Left Side = Right Side |
|
There are trinomials of the form x2 + bx + c that cannot be factored over the integers. In the case of
x2 + x – 1, for example, there is no pair of integers whose sum is 1 and whose product is –1.
----------------------------------------------------------------------------------
![]() Tip
Tip
When a polynomial cannot be factored such that the factors include only integer coefficients, we say that the polynomial cannot be factored over the integers.
--------------------------------------------------------------------------------------------
![]() Try This 5
Try This 5
Practice applying the methods of factoring trinomials. Complete the following in your course folder ( binder), showing all work
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 5. Complete “Exercises” questions 4, 14.a), 14.c), 14.e), 14.g), 15.d), 21.b), 21.d), and 21.f) on pages 166 and 167.
Use the link below to check your answers to Try This 5.
Possible TT5 (Try This 5) Solutions
![]() Self-Check
Self-Check
As you practice factoring using the methods that you have learned in this lesson, you should be aware of some common errors that can occur in their application. Some of these errors are due to inattention to details but do not imply student misunderstanding. Other types of errors reveal a misconception of the recently learned math principles.
The following examples show how a student may factor a polynomial using the methods learned in this lesson. In each case, the student has made an error. Your job is to identify and to correct the error.
SC 3. Study the solutions and identify the error that has been committed. Then correct the error and complete the solution.
- Factor 10x3 + 15x2 + 5x.
10x3 + 15x2 + 5x = 5x(2x2 + 3x) - Factor x2 – 5x – 6.
Find two numbers whose product is –6 and whose sum is –5. The numbers are –3 and –2. Therefore, the factors are (x – 3)(x – 2). - Factor 2x2 + 2x – 24.
Find two numbers whose product is –24 and whose sum is 2. The numbers are 6 and –4. Therefore, the binomial factors are (x – 4)(x + 6).
![]() Try This 6
Try This 6
Identify the error and correct the solution. How can a student know if there is an error in his or her solution?
Complete the following in your course folder ( binder), showing all work
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 6. a. Complete “Exercises” question 12 on page 155.
b. Compete “Review” question 14 on page 199.
Use the link below to check your answers to Try This 6.
Module 3: Polynomials
Connect
In this lesson you learned strategies that can be used to factor polynomials with common factors. You also learned how to factor a trinomial of the form x2 + bx + c. As you continue to learn new strategies for factoring different types of polynomials, you will want to keep track of these strategies in an organized fashion. Doing so will help you select the best method for factoring a given polynomial.
Open the Factoring Strategies document, and save (or copy it by hand). After each of lessons 3, 4 and 5 you can add to the document so that you have a summary of the different types of strategies for factoring and when to use which one.
![]() Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Assess tab or by using the Quizzes link under the Activities block. Also, ensure your work in your binder (course folder) is complete.
 Project Connection ** NOT ASSIGNED**
Project Connection ** NOT ASSIGNED**
In Module 2 you learned about substitution ciphers where each letter of the alphabet is represented by a corresponding number. An Atbash cipher is a substitution cipher where each letter of the alphabet is represented by another letter. The table below shows the substitutions for an Atbash cipher.

Example
Translate the ciphertext MFNYVI using the Atbash cipher
Solution
Using the table, substitute the letter that appears above or below each letter in the ciphertext to obtain the plaintext. Use the table that follows. The ciphertext is shaded green. The plaintext is shaded yellow.
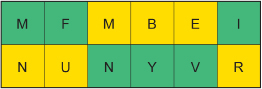
The plaintext is NUMBER.
The Atbash cipher can be rotated around like the tread on a treadmill. For example, you can shift it three positions clockwise. The resulting cipher looks like the following:

Notice that all 26 letters of the alphabet are still represented sequentially. The only difference is that A is not found at the beginning!
Example
Use the new version of the cipher to encrypt NUMBER.
Solution
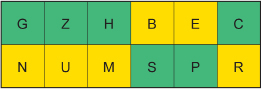
The ciphertext is GZHSPC.
You can create many variations of the same cipher just by rotating the original cipher clockwise any number of positions. In order for your message to be decoded properly, your recipient will need to know which variation of the cipher you used. You can do this by simply giving the recipient two letters that are in the same column. For example, you can give them G and N.
To add an additional level of security, you can encrypt those two letters as binomials. The following steps show a simple way to do this:
Step 1: Identify the position of each letter in the alphabet. Establish corresponding binomials.
|
Letter |
Position |
Binomial |
|
G |
7 |
x + 7 |
|
N |
14 |
x + 14 |
Step 2: Multiply the binomials to obtain a key for the encrypted message.
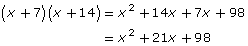
In this case, the sender would send the ciphertext along with the encrypted key. To decode the message, the recipient would have to
- factor the trinomial
- identify the letters represented by the binomials
- reconstruct the correct Atbash cipher variation based on those letters
- use the cipher to translate the message
Now go to the Unit 2 Project. Complete the Module 3: Lesson 3 portion of the project.
 Going Beyond
Going Beyond

© ZTS/shutterstock
Did you know that you can use your graphing calculator to verify that you have factored trinomials correctly?
To verify whether the factors are correct, follow the procedure:
Step 1: Enter the original polynomial into “Y1 =”.
Step 2: Enter the factored version into “Y2 =”.
Step 3: Execute the Graph command and observe carefully.
Step 4: If you see two distinct graphs, then the polynomial has been incorrectly factored. If the calculator graphs one graph on top of the other, then the polynomial has been graphed correctly.
Apply the above procedure to the following questions.
- Karim and Leona both factored x2 – 5x – 6.
Karim determined the factors to be (x – 2)(x – 3), whereas Leona determined the factors to be (x – 6)(x + 1).
Use a graphing calculator to verify their solutions. - Select two questions from your Lesson 3 Assignment where you were asked to factor a polynomial. Verify your solution using your graphing calculator.
In future math courses, you will learn more about how using a graphing calculator can not only help you to verify factoring but also to help you solve any equation.
Module 3: Polynomials
Lesson 3 Summary
In Lesson 3 you investigated the following questions:
- How are polynomial-factoring strategies similar to strategies used to obtain the prime factorization of a whole number?
- How can you tell if a polynomial is factored correctly?
In this lesson you learned how to find the common factors of a polynomial. Like the prime factorization that you learned in Module 2, you can also break monomials into their prime and variable factors. By doing so, you can apply the same techniques for generating the greatest common factor that you did with whole numbers. Alternatively, you could also list all of the factors of each term in a polynomial and select the greatest common factor from the lot.
In the previous lesson you verified your solutions by substituting a known numerical value to see if both sides of the expression would yield the same value. One of the key ideas in this lesson is that factoring is the reverse process of multiplying polynomials. Therefore, an alternate method for checking that the obtained factors are correct is to multiply the factors together. If the result is equal to the original polynomial, then the factors are correct.
In the next lesson you will build upon the factoring strategies you have learned so far. You will explore strategies that can help you to factor trinomials of the form ax2 + bx + c, where a ≠ 1.