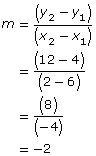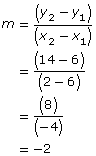Lesson 3: Parallel and Perpendicular Lines
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 3: Parallel and Perpendicular Lines |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 5:23 AM |
Module 6: Linear Equations
Lesson 3: Parallel and Perpendicular Lines
Focus

© aA./12578997/Fotolia
Piet Mondrian was a painter who lived in the early 1900s. Painting was his recreational pastime while he worked as a primary school teacher. Later, he would become famous for his artwork, particularly those he classified as Neo-Plasticism. Art in this style can be seen in the photo, where an irregular grid of parallel and perpendicular lines is painted on a white background. Some of the spaces in between are painted with the primary colours. Today, you can see this type of design in clothing, shoes, and stained glass artwork.
You have previously learned the definitions of parallel and perpendicular lines. In this lesson you will learn how the slopes of lines can be used to identify whether a set of lines is parallel, perpendicular, or neither. You will also learn how to determine the equations of lines that are either parallel or perpendicular to other lines. At the end of this lesson, you will have the opportunity to select and analyze a work of art for parallel and perpendicular lines.
Outcomes
At the end of this lesson, you will be able to
-
generalize and apply a rule for determining whether two lines are parallel or perpendicular
-
write the equation of a linear relation given the coordinates of a point on the line and the equation of a parallel or perpendicular line, and explain the reasoning
Lesson Questions
-
How can you determine the relative orientation of a pair of lines by examining their slopes?
-
How can knowledge of mathematical relationships between parallel and perpendicular lines be applied to problem-solving situations?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Activities block on the left in moodle or under the Assess tab.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 6: Linear Equations
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your binder. If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
Answers
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources either before or after you try the Are You Ready? questions. Your teacher may also direct you to this section to review specific concepts.
Use the Mathematics Glossary’s “Parallel” and “Perpendicular” to review terms. You can review the definitions or try the demonstration applets.
Parallel
-----------------------------
Perpendicular
----------------------------
Use the video titled “Slope intercept equation from two points ” to practice writing equations of linear functions.
Materials
You will need the following to complete Math Lab: Parallel and Perpendicular Lines:
-
grid paper
-
ruler or straightedge
-
index card or heavyweight paper
Module 6: Linear Equations
Discover
 Math Lab: Parallel and Perpendicular Lines
Math Lab: Parallel and Perpendicular Lines
Go Math Lab: Parallel and Perpendicular Lines, print it (or copy by hand) and complete it. Print the attached grid paper twice and have an index card handy to complete the second part.
Math Lab: Parallel and Perpendicular Lines
Grid Paper
Once you have completed these questions, use the link below to check your answers. Make any corrections or notes as needed. File this in your binder.
Module 6: Linear Equations
Explore

© Wirrsing/18737250/Fotolia
Parallel and perpendicular lines can be used as a tool for constructing art. A mural is a work of art that is painted or drawn on a large surface, such as a wall or a ceiling. A mural can be found on the exterior wall of a building or on an interior wall in buildings such as schools, hospitals, or art galleries. Murals are often enlarged versions of smaller pictures or photos. To transfer an image to the wall, one approach is to overlay a grid onto the source image. A larger, but corresponding grid would be constructed on the wall. In this way, the artist can concentrate on painting the image “one grid square at a time.”
In the case of the preceding picture, the artist has divided the mural into 30 smaller sections. Which section do you think would take the longest time to paint? Which one would not take very much time to paint?
In this lesson you will examine how the slopes of both parallel and perpendicular lines are related. You will then apply this knowledge to the construction of linear equations.
Glossary Terms
Add these terms and their definitions to the Glossary Terms section in your notes You may also want to add examples that demonstrate how each term is applied.
- converse statement
- negative reciprocal
- parallel lines
- perpendicular lines
-----------------------------------------
 Watch and Listen
Watch and Listen
Use the math is fun site Perpendicular and Parallel lines to get a further sense of parallel and perpendicular lines.
Pay close attention to the use of terminology, some of which might be new to you. Could any of these terms be used to improve your response to the analysis questions in the Math Lab?
You may have noticed in the Math Lab and in the site that the slopes of parallel lines are equal. This can be written as an if-then statement:
“If two lines are parallel, then their slopes are equal.”
Now consider the converse of this statement. The converse can be thought of as the reverse of this statement:
“If the slopes of two lines are equal, then they are parallel.”
Is this statement true? Find out by trying the next exercise.
 Try This 1
Try This 1
Complete the following in your binder.
Try This 1 Questions
Use the link below to check your answers to Try This 1.
Possible TT1 Solutions
Example 1
Line EF passes through E(6, 4) and F(2, 12). Line CD passes through C(6, 6) and D(2, 14). Are the lines parallel? Justify your answer.
Solution
Determine the slopes of each line.
|
Line EF |
Line CD |
|
|
|
Since the slopes are the same, the lines are parallel.
 Self-Check
Self-Check
You should have at least two sets of perpendicular lines from Part B of the Math Lab. Apply these questions to each set.
SC 1. Multiply the slopes of two perpendicular lines. What do you get?
SC 2. Describe the procedure you can follow to convert the slope of one line into the slope of another line that is perpendicular to the first one.
 Try This 2
Try This 2
Once you have completed SC 1 and SC 2 and reviewed the answers, complete TT 2. If you need some assistance completing the question, read the following My Guide section.
TT 2. Prepare a demonstration of a way to test the validity of this statement:
If two lines are perpendicular to each other, then their slopes will have a product equal to –1.
Include the following:
- Write down the steps you followed so that your teacher or another student can duplicate your procedure, if necessary.
- Explain why the strategy was used, and describe how it supports the validity of the statement.
Remember that if you need some assistance, you can check the My Guide section in the lesson that shows one way that you can approach this task.
Possible TT2 Solutions
My Guide (click on materials list to get a drop down list)
Materials
-
grid paper
-
protractor
Step 1: Plot a point with integer coordinates. Choose a point that is near the centre of the grid, though not necessarily the origin itself. Call this point A.
Step 2: Apply a slope of ![]() to your point to find and mark a second point B.
to your point to find and mark a second point B.
Step 3: Join the two points A and B with a line that spans across the entire grid.
Step 4: Choose a point on the line with integer coordinates. This can be one of the two points that have already been plotted or another point on the line. Call this point C.
Step 5: Use the ![]() method to apply a slope of
method to apply a slope of ![]() to point C. Locate the new point and call this point D.
to point C. Locate the new point and call this point D.
Step 6: Join the points C and D with a line that spans across the entire grid.
Step 7: Use a protractor to measure the angle of the lines at their point of intersection. Are the two lines perpendicular?
Step 8: State your conclusions about the validity of the statement, “If the slopes of two lines are negative reciprocals, or have a product of −1, then the lines are perpendicular to each other.”
Work through the next example to see how you can find the slope of a line given specific information about a second line.
Example 2
Determine the slope of a line that is perpendicular to the line passing through G(4, 6) and H(2, 3).
Solution
Determine the slope of line GH.
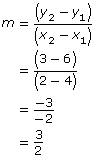
Then we can use
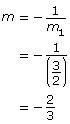
Therefore, the slope of the perpendicular line would be ![]()
 Tips
Tips
You already know that horizontal lines are perpendicular to vertical lines. Their slopes, however, are not readily identified as negative reciprocals. Therefore, you should keep in mind that a line with a slope of zero will always be perpendicular to a line with a slope that is undefined.
Module 6: Linear Equations
 Try This 3 - 4
Try This 3 - 4
Complete the following in your binder to practice identifying parallel and perpendicular lines.
Try This 3 - 4 Questions
Use the link below to check your answers to Try This 3 -4.
Possible TT3-4 Solutions
 Read
Read
Go to your textbook to find examples of how to identify both parallel and perpendicular lines.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Identifying Parallel Lines” on page 345. Next, read “Example 2: Examining Slopes to Compare Lines” on pages 346 and 347.
Before you look at the solutions to both of these examples, try to figure out the answers by studying the graphs. How important do you think it is to sketch a graph of the problem before trying to solve it?
 Watch and Listen
Watch and Listen
Use “Parallel and Perpendicular Line Segments Applet” as a way to check your understanding of the slopes of parallel lines and perpendicular lines. Scroll down to find the applet. Choose Parallel lines only first and then once you have played around for a while, choose Perpendicular lines only and play with that. Once you move a point, look to see what that does to the lines and in particular the slopes of the lines.
Once you have played with the applet, if you feel you need more work on this, scroll back UP to the top and click on the Parallel and Perpendicular Lines lesson for more solved examples.
 Try This 5
Try This 5
Complete the following in your binder.
TT5: Foundations and Pre-calculus Mathematics 10 (Pearson)
a. Complete “Exercises” questions 5, 6, 8.a), 8.b), 9.b), 9.c), and 17 on pages 349 and 350.b. Complete “Exercises” question 21 on page 364.
Use the link below to check your answers to Try This 5.
Possible TT5 Solutions
Let's have a look at an application question to help us work on our understanding of parallel and perpendicular lines.
Example 3:
For the pair of slopes, what is the value of n if the lines are parallel? What is the value of n if the lines are perpendicular?![]()
Solution:
When lines are parallel, their slopes are equal, so we can equate the slopes and solve.
When lines are perpendicular, the slopes are negative reciprocals. So the number of the right of 2 needs to be reciprocated and made a -1/2.
In previous lessons you learned how to write the equation of a linear function. You learned that you need to know the slope of the function as well as a point on the graph. These pieces of information are not always given directly.
For example, you have seen that you may have to use two points to determine a slope before you can write the equation of a line. You can also indirectly determine the slope of a line by using the given information about another line that is either parallel or perpendicular.
Example 4:
Write the equation of a line that passes through (1, 2) and is parallel to the line 2x - 3y + 10 = 0. Write the final answer in slope intercept form and general form.
Solution:
Step 1: Change the given line into slope intercept form, so the slope can be found:
Step 2: Use slope point form and find the equation in slope intercept form.
Step 3: Change slope intercept form to correct general form. ( remember, no fractions and A has to be positive)
 Read
Read
Go to your textbook to work through examples on how to write the equations of lines that are parallel or perpendicular to given lines.
Foundations and Pre-calculus Mathematics 10 (Pearson)
As you read the textbook example, try to answer the questions:
-
In what form(s) is the slope of the line easiest to determine?
-
How could you continue the work in the example to find the y-intercept?
Read “Example 4: Writing an Equation of a Line That Is Parallel or Perpendicular to a Given Line” on page 370.
 Self-Check
Self-Check
SC 3. Write the equation of a line parallel to the line y = 2x − 1 and that passes through (−5, 1).
SC 4. Write the equation of a line that passes through the point ![]() and is perpendicular to the line
and is perpendicular to the line ![]()
Compare your answers to SC3 and 4.
SC 5. For the pair of slopes, what is the value of n if the lines are parallel? What is the value of n if the lines are perpendicular?![]()
Compare your answers to SC5
 Watch and Listen
Watch and Listen
For more help on finding equations of parallel and perpendicular lines, watch this screen cast. There are also solved examples on the bottom left. Try This 6
Try This 6
Complete the following in your binder.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 6. Complete “Exercises” questions 20, 22, 24, 25, and 26 on page 374.
Use the link below to check your answers to Try This 6.
Possible TT6 Solutions
Module 6: Linear Equations
Connect
 Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Quizzes link to the left in moodle or under the Assess tab and ensure your work in your binder (course folder) is complete.
 Project Connection **NOT ASSIGNED**
Project Connection **NOT ASSIGNED**
In this project you will analyze a picture. Go to the Unit 4 Project and complete the Module 6: Lesson 3 component of the project.

© MBA –RF Mask
 Going Beyond
Going Beyond
Tangrams are Chinese puzzles that consist of seven pieces cut from a square. These shapes can be arranged to create different designs, some of which are shown in the diagram. Amongst the shapes in a tangram set are right triangles, a square, and a parallelogram.

© KamiGami/shutterstock
This image shows 12 tangram shapes. As a fun activity, you may use the “Tangram Template” to recreate as many of these shapes as possible.
Work with a partner to complete the following activity.
- Perform an Internet search to determine the formal definition of the following terms.
- right triangle
- parallelogram
- A quadrilateral (four-sided shape) is drawn on a coordinate plane. The corners are located at A(−4, 6), B(2, 5), C(0, −3), and D(6, −2).
- Plot the corner points and sketch the quadrilateral.
- Together with your partner, discuss how you could determine whether this shape represents a parallelogram based on its formal definition and also on the concepts learned in this lesson.
- Use your strategy to determine whether the quadrilateral is a parallelogram or not.
- A triangle has corner points at P(3, 10), Q(−6, 8), and R(6, −6).
- Plot the corner points and sketch the triangle.
- Together with your partner, discuss how you could determine whether this shape represents a right triangle based on its formal definition and also on the concepts learned in this lesson.
- Use your strategy to determine whether the triangle is a right triangle or not.
Save your work in this Going Beyond section to your course folder.
As a fun activity, download a copy of the “Tangram Template.” Cut out the seven shapes. Try to create as many of the twelve tangram designs as you can. Then create one of your own. Name and draw this shape; then challenge a friend to recreate it.
Save your results and designs in your course folder. Your teacher may want to examine them later.
Module 6: Linear Equations
Lesson 3 Summary
In this lesson you investigated the following questions:
-
How can you determine the relative orientation of a pair of lines by examining their slopes?
-
How can knowledge of mathematical relationships between parallel and perpendicular lines be applied to problem-solving situations?
In this lesson you examined the relationship between the slopes of parallel lines and between the slopes of perpendicular lines. You discovered that the slopes of parallel lines are equal. Conversely, if two lines with different y-intercepts have the same slope, they are parallel to one another. You also learned that the slopes of perpendicular lines are negative reciprocals of each other.
For example, if the slope of one line is ![]() then the slope of a line that is perpendicular to the first is −2. The product of a pair of negative reciprocals is −1.
then the slope of a line that is perpendicular to the first is −2. The product of a pair of negative reciprocals is −1.
The converse statement is also true: If the slopes of two lines are negative reciprocals of each other, then the lines are perpendicular to each other.
In the last lesson you learned how to use a line’s slope and points to determine its equation.
In this lesson you continued to practise writing linear equations. You were not always given information about the slope and points directly. In this lesson you worked with a partner to develop strategies for extracting the information that you need to construct equations. These strategies may have included rearranging an equation in order to uncover its slope or its y-intercept. As well, you may have chosen to graph a line in order to help you determine its properties. Knowing the information that you need is a vital first step in solving a mathematical problem. The second step is to recognize the information that can be provided by the problem constraints.
In the next lesson you will learn how to apply linear equations to problem-solving situations. You will combine all of the concepts that you have learned in this module. You will use function notation to model linear relations, construct equations based on given information, and use those equations to determine solutions.