Lesson 4
| Site: | MoodleHUB.ca 🍁 |
| Course: | Math 20-3 SS |
| Book: | Lesson 4 |
| Printed by: | Guest user |
| Date: | Tuesday, 2 December 2025, 7:01 AM |
Description
Created by IMSreader
1. Lesson 4
Module 4: The Right Kind Of Triangles
Lesson 4: Solving Problems Involving Two or More Right Triangles
Focus

iStockphoto/Thinkstock
The Noorduyn Norseman was once a familiar sight in the Canadian North. This floatplane, which was designed to serve northern communities, was built in Canada between 1935 and 1959. There are still Norseman planes transporting cargo and passengers. As a tribute to this aircraft and the bush pilots who flew them, every summer there is a Norseman Floatplane Festival at Red Lake, Ontario.
Bush pilots flying over wilderness lakes and forests must know their position at every moment. Did you know that trigonometry is a fundamental tool for for navigating in the air?
In this lesson you will learn to navigate through trigonometric problems involving two or more right triangles.
Lesson Question
In this lesson you will investigate the following question:
- How are problems involving two or more right triangles solved?
Assessment
Your assessment for this lesson may include a combination of the following:
- course folder submissions from the Try This and Share sections of the lesson
- your contribution to the Mathematics 20-3: Glossary Terms
- Lesson 4 Assignment (Save a copy of your lesson assignment to your course folder now.)
- the Project Connection
Materials and Equipment
- calculator
- tape measure
- clinometer (made in Lesson 3)
1.1. Launch
Module 4: The Right Kind Of Triangles
Launch
This section checks to see if you have the necessary background knowledge and skills required to successfully complete Lesson 4.
Launch will review the following topics:
- solving a right triangle
- representations of slopes
Complete the following Are You Ready? questions. If you have difficulty or any questions, visit Refresher for a review or contact your teacher.
1.2. Are You Ready?
Module 4: The Right Kind Of Triangles
Are You Ready?
In previous mathematics courses you solved right triangles. To solve a right triangle means to find all of its missing measurements when given a side and an angle or two sides. Remember, the six parts of a triangle are the three sides and the three angles. Solving a right triangle is a necessary skill in applying trigonometry in problem situations.
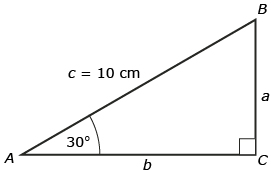
- Solve
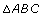 given ∠A = 30°, ∠C = 90°, and c = 10 cm.
given ∠A = 30°, ∠C = 90°, and c = 10 cm.
Answer
- Solve
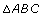 given ∠C = 90°, b = 5 cm, and c = 13 cm. Round to one decimal place if necessary.
given ∠C = 90°, b = 5 cm, and c = 13 cm. Round to one decimal place if necessary.
Answer
- Sketch a labelled diagram to represent a slope of 2.87%. Label the legs of the triangle with possible lengths. Answer
- Sketch a labelled diagram to represent a 3:7 roof pitch. Label the legs of the triangle with possible lengths. Answer
1.3. Refresher
Module 4: The Right Kind Of Triangles
Refresher
If you don’t know the answers in Are You Ready?, or if you require more information, do some review of solving a right triangle and slope representations.
Solving a Right Triangle
|
© 2010 Province of BC |
Slope Representations |
|
Go back to Are You Ready?, and try the questions again. Contact your teacher if you continue to have difficulty with the questions.
1.4. Discover
Module 4: The Right Kind Of Triangles
Discover
In Lesson 3 you used your clinometer to find the height of a totem pole or another pole, like a light standard. In the next Try This activity you will again look to find the height of a pole, but this time you will not be standing on the ground!
Try This 1
You are given the following diagram showing a flagpole outside a second-storey window. Use the information in the diagram to answer the following questions.
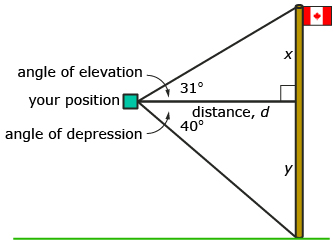
- In the diagram, there is one piece of information missing. What is needed before you can determine the height of the flagpole?
- How would you explain the steps involved in solving this type of trigonometric problem?
- Why were two triangles used to illustrate and solve this problem? Could the problem have been solved using one triangle? Explain your answer.
![]() Save your work to your course folder.
Save your work to your course folder.
Share 1
Share your responses to the questions in Try This 1 with a classmate or in a group.
- How did the strategy you used to solve this problem compare with others? Would you use the same strategy or change your strategy based on the discussion you’ve had?
- What are the similarities and differences between the problems in Try This 1 and the Try This 1 in Lesson 3, where you used your clinometer to find the height of a tall object?
![]() If required, save a copy of your discussion and your diagram in your course folder.
If required, save a copy of your discussion and your diagram in your course folder.
1.5. Explore
Module 4: The Right Kind Of Triangles
Explore
In previous lessons you solved problems using triangles and trigonometry. In this lesson you will encounter problem situations that need two triangles sharing sides or angles to help you find solutions.
Try This 2
Being a landscaper requires strong mathematical estimation and calculation skills. When planting trees, initially supporting them to develop a strong root base is essential to the development of the tree. Knowing how much guy wire is needed in order to support a tree is important.
Open the Guy Wire interactive to help calculate how much guy wire is needed to support the tree shown.
- Come up with a plan for how you can determine the amount of guy wire required to support the tree.
- Which angles would you measure to make your calculations? Use the protractor to measure the angles.
- Draw a diagram with all of the known and unknown sides and angles. Label the unknowns with a variable.
- What strategies could you use to calculate the unknown sides?
- How would you determine how much guy wire is needed to support this tree?
![]() Save a copy of your responses to your course folder.
Save a copy of your responses to your course folder.
Share 2
Share your results to Try This 2 questions 1 to 5 with a partner or in a group.
How do the strategies used to solve this problem compare? Would you change your strategy based on seeing the different strategies used?
![]() If required, save a record of your discussion in your course folder.
If required, save a record of your discussion in your course folder.
1.6. Explore 2
Module 4: The Right Kind Of Triangles
Example
A dual pitch truss is used in the construction of a large shed. The shallow pitch is 26.57° (or 6:12). The steep pitch is 36.87° (or 9:12) and has a side length of 10 ft. The truss shown in the diagram is positioned at one end of the shed, called the gable end. The gable end will be covered by plywood after framing the shed. On the diagram, the perimeter of the gable end is outlined in red. How much plywood is needed to cover this triangular area? Round your answer to the nearest tenth of a square foot.
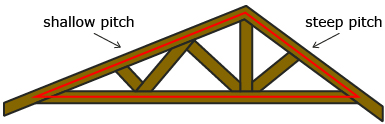
Solution
Watch Roof Truss to see how the problem can be solved. The Adjacent Right-Triangle Problem demonstration is another example of how a problem involving two triangles can be solved using trigonometry.

Self-Check 1
Solve for the unknown in the following adjacent right-triangle problem. You may choose to revisit the Adjacent Right-Triangle Problem demonstration for help.
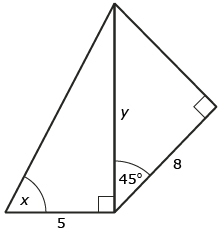
Answer
1.7. Explore 3
Module 4: The Right Kind Of Triangles

Digital Vision/Thinkstock
Check out another problem situation that can be solved using two triangles. Can you think of another situation where two triangles might help solve a problem?
Example
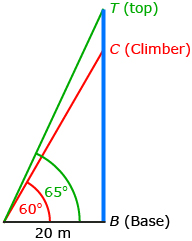
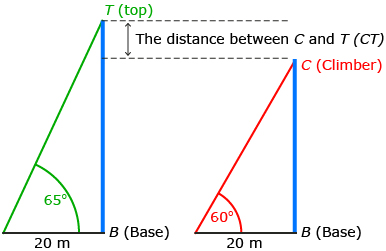
From a point 20 m from the base of a vertical ice wall, the angle of elevation of a climber is 60°. From the same point, the angle of elevation of the top of the wall is 65°. How many more metres must she climb to reach the top? Round to one decimal place.
Solution
| Draw and label a diagram to represent the problem. |
|
You must determine the distance between C and T. |
CT = BT − BC
|
First find BT.
Use the larger right triangle with the 65° acute angle.
Don’t round until you have made your last calculation. |
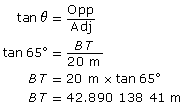 |
Next, find BC.
Use the smaller right triangle with the 60° acute angle. |
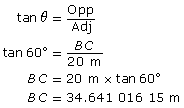 |
Now find the distance CT. The climber has approximately 8.2 m to reach the top. |
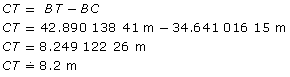 |
If you would like to review another example of a problem that uses two triangles in the solution, turn to page 172 of MathWorks 11 and work through “Example 2.”
Self-Check 2
- Turn to page 177 of MathWorks 11. Do “Build Your Skills” question 1. Answer
- Turn to page 178 of MathWorks 11. Do “Build Your Skills” question 4. Answer
- Turn to page 179 of MathWorks 11. Do “Build Your Skills” question 6. Answer
It is now time to add new math terms and notes to Mathematics 20-3: Glossary Terms.
In this lesson the new terms and notes you will add are
- solving a right triangle
- parts of a triangle
1.8. Connect
Module 4: The Right Kind Of Triangles
Connect
Going Beyond
Examine the diagram below and answer the following questions.
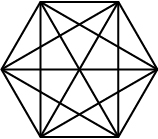
- How many right triangles are there in the figure?
- How did you arrive at your answer?
Project Connection
You are now ready to complete Part B: At Play—Stained Glass Sailboat of the Module 4 Project.
Remember to save all your work to your course folder to submit at the end of the module.
Lesson 4 Assignment
Your lesson assignment contains some problems for you to solve using knowledge gained during the lesson. Now you will have the chance to apply the concepts and strategies that you have learned to a new situation.
Open your Lesson 4 Assignment that you saved to your course folder and complete the questions. Please show work to support your answers.
1.9. Lesson 4 Summary
Module 4: The Right Kind Of Triangles
Lesson 4 Summary

iStockphoto/Thinkstock
Saskatoon, named after the Nehiyawak word for the purple berries found in abundance on the Prairies, is often called The City of Bridges. Seven major bridges span the South Saskatchewan River, which flows through the city.
The railroad bridge in the photograph incorporates in its construction multiple right triangles. The triangle is a geometric shape used in design for strength and stability.
Try your hand at bridge building. Using your favourite search engine, find a “build a bridge” activity and see what is required to properly build a bridge.
In this lesson you investigated how more than one right-angle triangle appears in a variety of applications. Right-angle triangle trigonometry was your bridge to understanding.