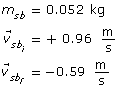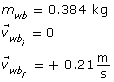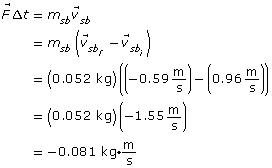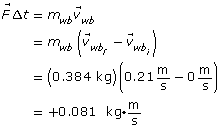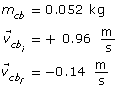Module 2
| Site: | MoodleHUB.ca 🍁 |
| Course: | Physics 30 SS |
| Book: | Module 2 |
| Printed by: | Guest user |
| Date: | Tuesday, 16 December 2025, 1:39 PM |
Description
Created by IMSreader
Table of contents
- 1. Module 2
- 1.1. Big Picture
- 1.2. In this Module
- 1.3. Lesson 1
- 1.4. Page 2
- 1.5. Page 3
- 1.6. Page 4
- 1.7. Page 5
- 1.8. Page 6
- 1.9. Page 7
- 1.10. Lesson 2
- 1.11. Page 2
- 1.12. Page 3
- 1.13. Page 4
- 1.14. Page 5
- 1.15. Page 6
- 1.16. Page 7
- 1.17. Lesson 3
- 1.18. Page 2
- 1.19. Page 3
- 1.20. Page 4
- 1.21. Page 5
- 1.22. Module Summary/Assessment
- 1.23. Module Glossary
1. Module 2
Module 2—The Conservation of Momentum in Isolated Systems
Module Introduction

Digital Vision/Getty Images
In this module, you will learn how to apply conservation principles related to momentum and energy in the analysis of one- and two-dimensional collisions.
The essential questions that you will be considering in this module are as follows:
-
How is the conservation of momentum principle applied to linear collisions?
-
Is it possible to describe mathematically the difference between elastic and inelastic collisions using kinetic energy?
-
How are the conservation of momentum principle and vector component analysis applied to solve non-linear collisions?
1.1. Big Picture
Module 2—The Conservation of Momentum in Isolated Systems
 Big Picture
Big Picture

S. Meltzer/Photolink/Getty Images
In Module 1 you explored the need for better-designed vehicle safety devices to keep our roads safe. If you have ever been in a car accident or know someone who has, you know that collisions can happen suddenly and are over very quickly. In some cases, experts are called in to decide who may be at fault and to establish responsibility for the associated costs of an accident. In this process, scientific principles such as the conservation of momentum are applied to develop an approximate reconstruction of the events just prior to a collision. This reconstruction is important for establishing why and how a collision occurred.
Consider what happens after a vehicle collision:
-
Two vehicles collide at an intersection. The vehicle mass is scattered about and various forces act, producing heat, sound, and deformation of metal, plastic, and glass. The tires skid across the pavement and chunks of debris are thrown upwards into the sky. Hot metal fragments cool down as the wreckage waits to be cleared.
-
An ambulance arrives at the scene to treat the injured. The police take numerous photographs of the scene, measure skid marks, and note the temperature and road conditions. Investigators estimate vehicle masses and note debris patterns.
-
Investigations determine relevant events at the time of the collision and establish fault.
The investigation into the events just prior to the collision is based on the conservation of momentum, a principle that perfectly describes collisions that occur in isolated systems. An isolated system is one in which no mass enters or leaves the system, and no net external force acts on it. You will learn more about this in a later lesson, but such a system is not readily found on our planet (curling stones on a totally frictionless sheet of ice would be a good approximation). And although we know cars don’t collide like curling stones, we could analyze car collisions in a similar way, assuming the system to be isolated just at the moment of impact. This assumption allows us to apply scientific principles to produce a reasonable approximation of events for a vehicle crash. In this module we will learn how to use the conservation of momentum to analyze and reconstruct collisions in both one and two dimensions.
Case File

© Katherine Welles/shutterstock
On October 1, Kathy Johnson (not her real name) was driving home from work in her red car. As she approached the University Drive intersection, Bill Peterman (not his real name), driving his white pickup truck, attempted to cross the same intersection on his way to class. Unfortunately, they collided in the centre of the intersection.
As seen in this photo, both vehicles became joined and moved off to the side of the intersection before coming to rest. When the police arrived and began taking statements, Bill claimed that Kathy was well back from the intersection when he attempted to cross and that her high rate of speed was to blame for the accident. At the same time, Kathy insisted she was travelling at the posted speed limit, 50 km/h, and that Bill entered the intersection without proper care and attention.
Both Kathy and Bill received medical attention for non-life-threatening injuries. The property damage to both vehicles was substantial. The case is now before the courts to decide who will pay for the damages. In addition, the police have charged Kathy with driving in excess of the posted speed limit.
In her defence, Kathy has hired a consultant to perform a crash analysis hoping that it will confirm her speed prior to the collision. The intent of this analysis is to prove, beyond a reasonable doubt, that she was actually travelling at the speed limit just prior to the accident. How is this possible? How can conservation principles related to momentum and energy be applied to analyze and understand collisions?
You will refer to this case study as part of your Module 2 Project throughout the lessons of Module 2.
Essential Questions
As you are working in Module 2, keep the following questions in mind:
-
How is the conservation of momentum principle applied to linear collisions?
-
Is it possible to describe mathematically the difference between elastic and inelastic collisions using kinetic energy?
-
How are the conservation of momentum principle and vector component analysis applied to solve non-linear collisions?
 Module Assessment
Module Assessment
Each lesson has a teacher-marked assignment, based on work completed in the lesson. In addition, you will be graded on your contributions to the Discuss section of each lesson.
You will also be asked to complete Self-Check or Try This questions, which you should place in your Physics 30 course folder. These are not formally assessed but are a valuable way to practise the concepts and skills of the lesson. These activities can provide you with reflective feedback on your understanding of the lesson work.
You will be marked for your lesson work on the following items:
-
Module 2: Lesson 1 Assignment
-
Module 2: Lesson 2 Assignment
- Module 2: Lesson 3 Assignment
-
Module 2 Project
In each lesson you will prepare a crash analysis for your Module 2 Project of the collision between Kathy and Bill described in the Big Picture section. The analysis should be complete at the end of Lesson 3. It must show a complete solution for the mathematical determination of Kathy's speed just prior to the collision. If you have any questions contact your teacher.
1.2. In this Module
Module 2—The Conservation of Momentum in Isolated Systems
In This Module
Lesson 1—Linear Collisions and the Conservation of Momentum
In this lesson you will explore the conservation of momentum in linear collisions. You will explore linear collisions in the context of the following questions:
-
Can the complicated details of a linear collision be eliminated during the analysis of an interaction?
-
What is the law of conservation of momentum? How can this law be applied?
Lesson 2—Kinetic Energy and Collisions
In this lesson you will explore the difference between elastic and inelastic collisions in terms of energy changes and the conservation of momentum. You will explore elastic and inelastic collisions in the context of the following questions:
-
How can the kinetic energy of the objects in a system before and after a collision be used to categorize the type of collision?
-
What is the fundamental difference between an elastic and an inelastic collision?
-
In a collision between two automobiles, is it better for the occupants if the collision is elastic or inelastic?
Lesson 3—Analyzing Non-Linear Collisions
In this lesson you will apply the conservation principle and component analysis to analyze non-linear collisions. You will explore collisions of this nature in the context of the following questions:
-
Is momentum conserved in a non-linear collision?
-
How is component analysis applied to solve non-linear collision problems?
1.3. Lesson 1
Module 2—The Conservation of Momentum in Isolated Systems
Lesson 1—Linear Collisions and the Conservation of Momentum

©Aleksandar Kamasi/shutterstock
 Get Focused
Get Focused
It is obvious that this photo shows a rear-end collision. The vehicles collided along a straight line—a linear collision.
During the collision, the momentum of each of the cars involved changed, and forces acted over time to provide an impulse to each car. These interactions are complicated; the forces not only changed the momentum of each vehicle, the forces also changed the shape of each vehicle. It is worthwhile to analyze interactions like this not only to determine who was responsible from a legal point of view, but also to improve the design of vehicles to reduce injuries to the occupants.
momentum: the product of the mass and velocity of an object
In this lesson you will explore linear collisions in the context of the following questions:
-
Can the complicated details of a linear collision be eliminated during the analysis of an interaction?
-
What is the law of conservation of momentum, and how can it be used to answer the previous question?
-
Under what circumstances can this law be applied?
 Module 2: Lesson 1 Assignments
Module 2: Lesson 1 Assignments
Your teacher-marked Module 2: Lesson 1 Assignment requires you to submit a response to the following:
- Lab—LAB 1, LAB 2, and LAB 3
-
Assignment—A 1, A 2, and A 3
-
Discuss—D 5
Although the other questions in this lesson will not be marked by the teacher, you should still answer these questions. The Self-Check and Try This questions are placed in this lesson to help you review important information and build key concepts that may be applied in future lessons.
After a discussion with your teacher, you must decide what to do with the questions that are not part of your assignment. For example, you may decide to submit to your teacher the responses to Try This questions that are not marked. You should record the answers to all the questions in this lesson and place those answers in your course folder.
You will also begin your Module 2 Project. You will start working on a Crash Analysis, which you will save to your Physics 30 course folder and submit to your teacher for marks when you have finished Module 2.
1.4. Page 2
Module 2—The Conservation of Momentum in Isolated Systems
 Explore
Explore
 Read
Read
Read “Collisions in One Dimension” on pages 468 to 470 of your physics textbook for an introduction to collisions of systems of objects.
Understanding Isolated and Non-isolated Systems

Lawrence M. Sawyer / Sports and Recreation 2/Getty Images
A system is a collection of two or more objects. For example, a collection of curling stones on a sheet of ice represents a system. If the number of stones on the ice does not change, the system is closed. If there were no external forces acting on the stones, such as the players pushing them or the small amount of friction on the ice, the system would also be isolated.
There are other kinds of systems as well, some of which you may be familiar with.
In the open system, mass and energy may enter or leave the system, and external forces may influence the system. In the closed system, no mass enters or leaves the system but energy can. Also, external forces may influence the closed system. No net external force acts on the isolated system, and no mass or energy enters or leaves the system.
|
|---|
A truly isolated system is impossible to create. Isolating a system in terms of mass is fairly straightforward. However, isolating the system with respect to energy and external forces, especially gravity, is far more difficult. For questions in Physics 30 it is assumed that the system is isolated from net external forces in order to simplify questions.
|
In this lesson when we examine the momentum of a system, it is important that the system under investigation is an isolated system. Assumptions are often made that the force of friction acting in a system is negligible, thereby providing a useful model for approximating real world situations, such as vehicle collisions.
It is easy to tell if a system is closed: no mass enters or exits. However, it is a bit more difficult to determine if a system is isolated—you must be aware of any external forces that may be acting on the system. Here are some examples:
Example 1
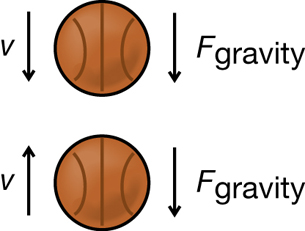
Two basketballs (the system) are moving vertically in the air. One of the balls is falling down, while the other has just been thrown upward. The two balls collide as they move.
The system is not isolated. The external force acting on both balls is the force of gravity.
Example 2
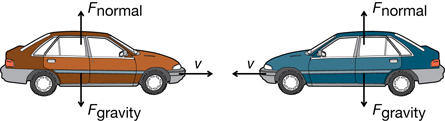
Two cars (the system) are driving toward one another on smooth pavement and collide head on.
If we assume that the force of friction is negligible, this system can be treated as isolated. Interestingly, in the vertical plane, the normal force of the road balances the force of gravity, so there is no net external force in the vertical plane.
Example 3
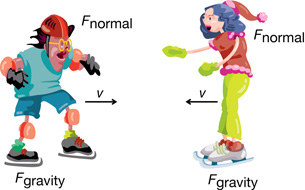
Two skaters (the system) are coasting along frictionless ice and are headed straight for each other. They end up crashing into each other.
If we assume that the force of friction is negligible, this system can be treated as isolated. Again, there is no net external force acting in the vertical plane.
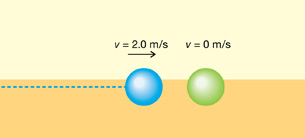
Module 1: Lesson 1 explained that any moving object has velocity and momentum. But what happens if two or more objects collide? What happens to the velocity and the momentum of each object? Let’s explore this question using a simulation of a rear-end collision.
1.5. Page 3
Module 2—The Conservation of Momentum in Isolated Systems
 Lesson 1 Lab: Elastic Collisions Lab
Lesson 1 Lab: Elastic Collisions Lab
Problem
Is momentum conserved in a linear collision?
Procedure
-
Perform five different collisions using the Collision 1D simulator, and complete the data tables in Observations.
-
For clarity on the simulator, toggle “Show CM” and “Show CM Frame” to the off position (
 ).
).
-
To generate a new collision, click the “New” button (
 ) and change the initial velocity of the blue ball by adjusting the velocity slider (
) and change the initial velocity of the blue ball by adjusting the velocity slider ( ) to any value.
) to any value.
-
After each collision, view the collision information by clicking the “Data” button (
 ) and fill in the appropriate table.
) and fill in the appropriate table.
-
The following equations will be required to complete the tables:
 and
and 
Observations
Collision 1 (Sample Data) |
||||||||||||
Object |
mass |
|
|
|
|
|
|
|||||
blue |
4.0 |
+8.0 |
−0.86 |
−8.86 |
+32 |
−3.44 |
−35.44 |
|||||
green |
9.0 |
0 |
+3.94 |
+3.94 |
0 |
+35.46 |
+35.46 |
|||||
Collision 2 |
||||||||||||
Object |
mass |
|
|
|
|
|
|
|||||
blue |
|
|
|
|
|
|
|
|||||
green |
|
|
|
|
|
|
|
|||||
Collision 3 |
||||||||||||
Object |
mass |
|
|
|
|
|
|
|||||
blue |
|
|
|
|
|
|
|
|||||
green |
|
|
|
|
|
|
|
|||||
Collision 4 |
||||||||||||
Object |
mass |
|
|
|
|
|
|
|||||
blue |
|
|
|
|
|
|
|
|||||
green |
|
|
|
|
|
|
|
|||||
Collision 5 |
||||||||||||
Object |
mass |
|
|
|
|
|
|
|||||
blue |
|
|
|
|
|
|
|
|||||
green |
|
|
|
|
|
|
|
|||||
 Module 2: Lesson 1 Assignment
Module 2: Lesson 1 Assignment
Remember to submit the answers to LAB 1, LAB 2, and LAB 3 to your teacher as part of your Module 2: Lesson 1 Assignment.
Analysis
LAB 1.
-
Is there a relationship between the changes in velocity of the blue mass and the green mass? If yes, describe the relationship.
-
Is there a relationship between the changes in momentum of the blue mass and the green mass? If yes, describe the relationship.
You should see an interesting connection between the changes in momentum of each mass: the changes in momentum should be equal, but opposite. For example, if the blue mass has an increase in momentum, then the green mass has a decrease in momentum by the same amount. This connection leads us to an important concept about momentum and what happens to the total momentum of a system in a collision.
LAB 2. If the change in momentum of one object is exactly equal but opposite to the change in momentum of another object, what does that indicate about the total momentum of the system?
LAB 3. If the total momentum of a system before a collision is equal to the total momentum of a system after a collision, then momentum is conserved. For each of the five collisions, verify that the total initial momentum is equal to the total final momentum by completing the following table.
Notice the following shorthand way of talking about the sum of the momentums of the blue and green masses. The capital Greek letter sigma (Σ) is often used to denote sums.
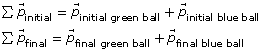
Collision |
Total Initial
(kg·m/s) |
Total Final (kg·m/s) |
Is Momentum Conserved? |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
Based on the lab activity, you should have found that the total momentum is conserved in a collision within an isolated system.
1.6. Page 4
Module 2—The Conservation of Momentum in Isolated Systems
The Law of Conservation of Momentum
For any isolated system, the total momentum does not change. In a collision, momentum is conserved—the total momentum before the collision is equal to the total momentum after the collision. Expressed as an equation, the law of conservation of momentum is
![]()
sum of initial momentum = sum of final momentum
The conservation principle can also be expressed algebraically as follows:
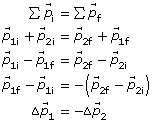

© Djordje Komljenovic/shutterstock
The law of conservation of momentum governs all physical interactions. It is considered to be one of the fundamental laws of physics. The law has been used to investigate and analyze all types of interactions. In addition to vehicle accidents, it has been used in the study of subatomic particles, such as electrons and protons, all the way up to the astronomical study of planets, stars, and galaxies.
This law controls the universe by keeping the total quantity of motion in the universe fixed. That is, if one body slows down and comes to rest, another body must speed up and start moving. Newton’s cradle of swinging masses is a good example of this, as you can see in the picture on the right.
 Watch and Listen
Watch and Listen
View The Conservation of Momentum video, which describes how Rene Descartes’ knowledge of straight lines led him to develop the law of conservation of momentum.
Analyzing Collisions
In the lab section you discovered that the total momentum of a system is conserved, as long as there are no external forces acting on a system. The conservation of momentum will be used to analyze various collisions. When solving problems, it is useful to follow the GRASP model for problem solving.
The GRASP model is on page 867 in your textbook.
 Self-Check
Self-Check
Verify your answers, where possible, by using the Collision 1D simulator.
SC 1. A 5.0-kg object is travelling to the right at 10.0 m/s. It collides with a 7.0-kg object that initially is at rest. After the collision, the 5.0-kg object continues to move to the right, but at 1.17 m/s. In what direction and with what speed is the other object moving?
 Self-Check Answers
Self-Check Answers
SC 1.
Given
mass 1 m1 = 5.0 kg
mass 2 m2 = 7.0 kg
mass 1 initial velocity ![]()
mass 2 initial velocity ![]()
mass 1 final velocity ![]()
Required
The final velocity of the 7.0-kg object ![]() .
.
Analysis and Solution
Choose the two objects as an isolated system. Since the 7.0-kg object is stationary, its initial momentum is 0.
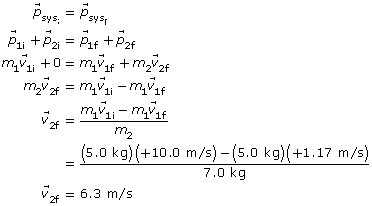
Paraphrase
The final velocity of the 7.0-kg object is 6.3 m/s.
1.7. Page 5
Module 2—The Conservation of Momentum in Isolated Systems
 Try This
Try This
Verify your answers, where possible, by using the Collision 1D simulator.
TR 1. When you shoot a gun, it "kicks back," or recoils.
- Using conservation of momentum, explain why a gun recoils when you shoot it.
- If a 30-g bullet is shot with a velocity of +300 m/s from a 7.5-kg gun, what is the recoil velocity of the gun?
 Module 2: Lesson 1 Assignment
Module 2: Lesson 1 Assignment
Remember to submit the answers to A 1 and A 2 to your teacher as part of your Module 2: Lesson 1 Assignment.
A 1. Object A, with a mass of 2.0 kg, is travelling to the right at 15.0 m/s. Object B, with a mass of 12.5 kg, is also travelling at 15.0 m/s, but to the left. If the two objects stick together upon impact, what is the final velocity of the system?
A 2. A 250-g firecracker explodes into two pieces. The first piece has a mass of 97 g and flies off to the right at 16 m/s. What is the velocity of the second piece?
 Self-Check
Self-Check
SC 2. An object, initially travelling to the right, collides with another object that is at rest. After the collision, the objects stick together and move to the left. Is this collision possible? Explain why or why not.
 Self-Check Answers
Self-Check Answers
SC 2. This is not possible. The initial momentum of the system is to the right; therefore, the final momentum must also be to the right.
 Module 2: Lesson 1 Assignment
Module 2: Lesson 1 Assignment
Remember to submit the answers to A 3 to your teacher as part of your Module 2: Lesson 1 Assignment.
A 3. Are the following collisions possible? Explain why or why not.
- Object A, initially travelling to the right, collides with object B, which is at rest. After the collision, object A moves back to the left and object B remains at rest.
- Object A, initially travelling to the right, collides with object B, which is at rest. Object B has more mass than object A. After the collision, object A moves back to the left and object B moves to the right.
- An object is travelling to the right and collides with another object that is at rest. After the collision, both objects travel to the right, but at different speeds.
 Read
Read
Read “Momentum is Conserved in One-dimensional Collisions” on pages 473 to 475 of your physics textbook.
Newton’s second and third laws can be used to derive the equation for impulse. In fact Newton’s original writings defined force in terms of momentum and time, not the ![]() that we used in Physics 20. However you haven’t done the calculus that is required to understand Newton’s original definition of force.
that we used in Physics 20. However you haven’t done the calculus that is required to understand Newton’s original definition of force.
 Try This
Try This
TR 2. Answer questions 1, 2, 5, 6, and 7 of “9.3 Check and Reflect” on page 486 of your physics textbook.
1.8. Page 6
Module 2—The Conservation of Momentum in Isolated Systems
 Reflect and Connect
Reflect and Connect

© Losevsky Pavel/shutterstock
In traffic, when one car fails to stop or slow down for another car, a rear-end collision can occur. When this happens, some of the momentum of the moving car is transferred at the moment of impact to the car it strikes. The conservation of momentum can be used to describe how this happens. But it is not that simple; vehicles on a roadway are not an example of an isolated system. Frictional forces interact during and after the collision to bring all the vehicles to a stop. Therefore, the analysis of the momentum would be most useful for determining speeds immediately before and after the point of impact, and no more.
 Module 2: Lesson 1 Assignment
Module 2: Lesson 1 Assignment
Remember to submit the answers to D 5 to your teacher as part of your Module 2: Lesson 1 Assignment.
 Discuss
Discuss
Now that you know about the law of conservation of momentum, you can apply what you have learned to a number of simplified forensics engineering problems. Post your answers to these problems to the discussion area to see how your answers compare to those of other students.
A collision occurred when a 1500-kg car collided with a 15 000-kg truck initially at rest. After the collision, the vehicles locked together and moved with a combined velocity of 1.0 m/s, east.
D 1. What type of collision is described by this situation?
D 2. Use the law of conservation of momentum to solve for the velocity of the car, in metres per second, before the collision occurred.
D 3. Convert your answer from D 2 into kilometers per hour. The posted speed limit in this area was 25 km/h because it was designated for loading passengers and freight. Was the car speeding?
D 4. In answering this question you have made some assumptions. Knowing this, would those assumptions be grounds for reasonable doubt if there were a court case against the car’s driver due to damages caused by the collision? Post your answer to the discussion forum and read the other students’ postings.
D 5. Read the other students’ comments and then rewrite your own answer to D 4 and include a description of what you learned from the other students’ responses.
Discussion Scoring Guide
Discussion Scoring Guide
Principles involved: Conservation of momentum, isolated systems |
||||
Criteria |
Level 1 (Below Standard) |
Level 2 (Approaching Standard) |
Level 3 (Standard) |
Level 4 (Above Standard) |
Knowledge |
||||
Demonstrates understanding of the situation, physics principles and technology, and their connections. |
Demonstrates a vague and sometimes incorrect understanding of the physics principles involved. Obvious irrelevant or missing information. |
Demonstrates a basic understanding of the physics principles involved. May exhibit minor mistakes or vague information or application to the situation. |
Demonstrates a good understanding of the physics principles involved and applies them properly to the given situation. All necessary information is given. |
Demonstrates a superior understanding of the physics principles involved and their application to the situation. All applications are considered in detail. |
Reflection |
||||
The post shows reflection on one’s own and other students’ work. Contributes to the group discussion. |
Does not make an effort to participate. Seems indifferent to discussion. |
Occasionally makes meaningful reflections on the group’s efforts or discussions. Marginal effort is shown to become involved with the group or discussion. |
Frequently makes meaningful reflections on the group’s efforts and presents relevant viewpoints for consideration by the group. Interacts freely with group members. |
Regularly attempts to motivate the group discussion and delve deeper into concepts. Interacts freely and encourages all group members. |
Content and presentation of discussion summary |
||||
The information is logically arranged in a clear and concise manner. |
The information is poorly organized with many concepts implied. Irrelevant or rambling sentences make reading difficult. |
The information is somewhat organized with implied concepts. Excessive words or awkward sentences are used, which hinder reading. |
The information is well-organized and logically arranged. All concepts are explicitly explained. There are a few awkward but understandable sentences. |
The information is well- organized and very easy to understand. Well-worded sentences make reading pleasurable. |
 Reflect on the Big Picture
Reflect on the Big Picture

© Katherine Welles/shutterstock
Recall the collision of Kathy and Bill from the Big Picture section. Based on what you learned in this lesson, start to analyze this collision.
Open the document titled Module 2 Project and store it in your Physics 30 course folder. You will be required to add to it at the end of each lesson in Module 2 until it is complete and submit it to your teacher as your Module 2 Project for marks.
Answer the following question in your crash analysis document:
The mass of the truck is 3200 kg, and the mass of the car is 2800 kg. Based on the length of the skid marks at the scene and the mass of the vehicles, police estimate that the combined mass was moving at 7.0 m/s just after impact. From this point, the two vehicles slid and came to rest at the corner of the intersection.
-
Determine the magnitude of the momentum just after the collision. (Analytic)
-
Is this the same as the magnitude of the momentum just before the collision? Explain why or why not. (Holistic)
Scoring Guide for Analytic Questions
Scoring Guide for Holistic Questions
Remember to store your new crash analysis document in your Physics 30 course folder.
 Module 2: Lesson 1 Assignment
Module 2: Lesson 1 Assignment
Remember to submit the Module 2: Lesson 1 Assignment to your teacher.
You should also have started working on your Crash Analysis document as part of your Module 2 Project.
1.9. Page 7
Module 2—The Conservation of Momentum in Isolated Systems
 Lesson Summary
Lesson Summary
At the start of this lesson, you were asked the following essential questions:
- Can the complicated details of a linear collision be eliminated during the analysis of an interaction?
- What is the law of conservation of momentum, and how can it be used to answer the previous question?
- Under what circumstances can this law be applied?
When collisions are analyzed in terms of momentum, the complicated conditions that exist during the fraction of a second that the collision occurs do not need to be considered. This approach involves identifying all the objects involved in the system and accounting for the momentum values of each object both before and after the collision.
If there are no external net forces acting on the system, then the system is said to be isolated and the law of conservation of momentum can be used to analyze the collision. This law states that the momentum of an isolated system remains constant:
![]()
The law of conservation of momentum is a powerful tool for analyzing collisions. It can be applied to any system that is isolated. In forensic engineering, the systems involving automobiles that crash are not friction-free. Strictly speaking, these systems are not isolated. Nevertheless, if the interaction forces involved in the collision are larger than the frictional forces, then the law of conservation of momentum can still be used to provide reasonably accurate descriptions of the conditions that occurred immediately before and after the crash.
Lesson Glossary
momentum: the product of the mass and velocity of an object
1.10. Lesson 2
Module 2—The Conservation of Momentum in Isolated Systems
Lesson 2—Kinetic Energy and Collisions
 Get Focused
Get Focused

left ©Frances Twitty/iStockphoto
right © Arthur Kwiatkowski/iStockphoto
What happens when a moving object strikes a stationary object? The answer to this question depends very much on the characteristics of the system of objects that are colliding.
Consider the case of the cue ball striking the purple ball on the pool table in the photograph on the right. If the collision occurs along a straight line, and spinning is kept to a minimum, then the cue ball will likely stop and the purple ball will move with very nearly the same velocity that the cue ball had prior to impact.
Would a similar chain of events occur when the blue car rear-ends the grey car in the other photo? In other words, would the grey car leave the point of impact moving with very nearly the same velocity of the blue car prior to impact? How does the system of the two cars differ from the system of the two balls on the pool table? What is the significance of the fact that the two cars undergo a permanent change in shape but the pool balls do not? The answers to these questions require you to consider the changes in kinetic energy that occur when a collision occurs within a system of objects.
In this lesson you will explore elastic and inelastic collisions within the context of the following questions:
-
How can the kinetic energy of the objects in a system before and after a collision be used to categorize the type of collision?
-
What is the fundamental difference between an elastic and an inelastic collision?
-
In a collision between two automobiles, is it better for the occupants if the collision is elastic or inelastic?
 Module 2: Lesson 2 Assignments
Module 2: Lesson 2 Assignments
Your teacher-marked Module 2: Lesson 2 Assignment requires you to submit a response to the following:
-
Lab—LAB 1 and LAB 2
-
Assignment—A 1, A 2, and A 3
You must decide what to do with the questions that are not marked by the teacher.
Remember that these questions provide you with the practice and feedback that you need to successfully complete this course. You should respond to all the questions and place those answers in your course folder.
You will also continue to add to your Module 2 Project that you started in Lesson 1 and saved in your course folder. The finished project will be submitted to your teacher for marks once you have completed Module 2.
1.11. Page 2
Module 2—The Conservation of Momentum in Isolated Systems
 Explore
Explore

© KUCO/shutterstock

© KUCO/shutterstock
Have you ever played with a device like this? It’s called Newton’s cradle. Spend a few moments playing with this animation of Newton’s cradle.
As you are playing, see if you can answer these questions:
-
What happens if you change the number of balls put into motion?
-
Do you ever get a different number of balls leaving the pack than enters it?
-
How does the velocity of the entering balls compare to the velocity of the leaving balls?
-
Notice the height at which the balls start their swing toward the pack. How does that initial height compare to the final height the balls reach when they swing away from the pack?
During your play with the animation, you surely saw that momentum was conserved. One ball enters and one ball leaves, and the velocities are basically the same. The same was true for two balls or even three. Momentum would have been conserved if one ball entered and two balls left with half the velocity of the original ball. Did that ever happen? (Knowing how the applet works makes the answer to that question an emphatic no!)
The answer to the last of the questions gives you a clue to what is happening. For example, you may have used just one starting ball. Since the starting height of the ball and the ending height of the ball seem to be the same, the energy seems to have been conserved. Just before impact, the energy of the moving ball can be calculated. You’ll remember the equation, ![]() . Just after the collision, the new moving ball will have the same kinetic energy. (These concepts would still be true if you had used more than one starting ball.) Kinetic energy appears to be conserved in Newton's cradle, but is kinetic energy always conserved in collisions?
. Just after the collision, the new moving ball will have the same kinetic energy. (These concepts would still be true if you had used more than one starting ball.) Kinetic energy appears to be conserved in Newton's cradle, but is kinetic energy always conserved in collisions?
|
|---|
The units for energy are joules (J), named after James Prescott Joule. The joule is not a base SI unit but is made of other SI units.
|
Is Kinetic Energy Conserved in a Collision?
Some of the energy in a closed, isolated system is in the form of kinetic energy. This is particularly true for two objects that collide, since one or both must be moving in order for this to occur.
 Self-Check
Self-Check
SC 1.Two bumper cars, each with a mass of 50 kg and travelling at 0.75 m/s, are headed straight toward each other.
-
What is the momentum of each car? Do the cars have the same momentum? (Remember: Momentum is a vector quantity.)
-
What is the total momentum of the system?
-
What is the kinetic energy of each car? Do the cars have the same kinetic energy? (Remember: Kinetic energy is a scalar quantity.)
-
What is the total kinetic energy of the system?
 Self-Check Answers
Self-Check Answers
SC 1.
a. 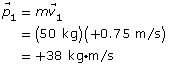
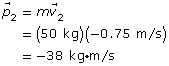
Each car has a different momentum. They are identical in magnitude but opposite in direction.
b. 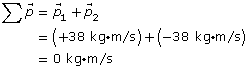
The total momentum of the system is zero.
c. 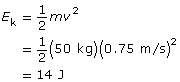
Both cars have the same kinetic energy because it is a scalar quantity.
d. 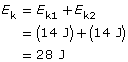
The total kinetic energy of the system is 28 J.
1.12. Page 3
Module 2—The Conservation of Momentum in Isolated Systems
Collisions and Kinetic Energy
In an isolated system, if the total energy is conserved, does this imply that the kinetic energy is conserved? Recall that kinetic energy is the energy of motion ![]() . Any object that is moving not only has momentum but also has kinetic energy. In previous lessons, you discovered that the total momentum of an isolated system is conserved during a collision. But what about kinetic energy—is it also conserved?
. Any object that is moving not only has momentum but also has kinetic energy. In previous lessons, you discovered that the total momentum of an isolated system is conserved during a collision. But what about kinetic energy—is it also conserved?
Lesson 2 Lab: Kinetic Energy and Collisions
In this lab, a simulation will be used to collect velocity and mass data from five different collisions. The data will be used to test the conservation of kinetic energy and momentum in each collision.
Problem
Are kinetic energy and momentum always conserved in an isolated system that involves the collision of two objects?
Procedure
-
Use the Collision 1D simulator to investigate five different collisions between the same objects and complete the table in LAB 1. The data collected will be used to verify that momentum is conserved and to determine if kinetic energy is also conserved.
-
On the simulation, toggle “Show CM” and “Show CM Frame” to the off position (
 ).
).
-
Click the “Options” buttons (
 ), and enter the settings shown here.
), and enter the settings shown here.
-
set e to “Random”
-
set Blue Mass to “Input” with a mass of 5.0 kg
-
set Green Mass to “Input” with a mass of 5.0 kg
-
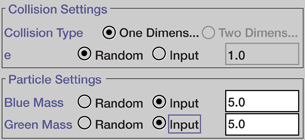
-
To generate a new collision (without changing the value of e or object mass), click the “New” button (
 ) and change the initial velocity of the blue ball by adjusting the velocity slider (
) and change the initial velocity of the blue ball by adjusting the velocity slider ( ) to any value.
) to any value.
-
After each collision, view the collision information by clicking the “Data” button (
 ) and fill in the appropriate table.
) and fill in the appropriate table.
 Module 2: Lesson 2 Assignment
Module 2: Lesson 2 Assignment
Remember to submit the answers to LAB 1 and LAB 2 to your teacher as part of your Module 2: Lesson 2 Assignment.
Observations and Analysis
LAB 1. In the chart below, record the initial velocity and final velocity for each object and the e value for the collision. Calculate the initial and final momentum and energy for each object using the mass and velocity values.
Do not worry about what e represents; it will be discussed in detail in the next section. The value of e will be listed with the other information on the simulation and must be recorded for each collision.
Collision 1 e = ____ |
|||||||
Object |
mass |
|
|
|
|
Ek initial |
Ek final |
blue |
5.0 |
|
|
|
|
|
|
green |
5.0 |
|
|
|
|
|
|
total |
----- |
----- |
----- |
|
|
|
|
Collision 2 e = ____ |
|||||||
Object |
mass |
|
|
|
|
Ek initial |
Ek final |
blue |
5.0 |
|
|
|
|
|
|
green |
5.0 |
|
|
|
|
|
|
total |
----- |
----- |
----- |
|
|
|
|
Collision 3 e = ____ |
|||||||
Object |
mass |
|
|
|
|
Ek initial |
Ek final |
blue |
5.0 |
|
|
|
|
|
|
green |
5.0 |
|
|
|
|
|
|
total |
----- |
----- |
----- |
|
|
|
|
Collision 4 e = ____ |
|||||||
Object |
mass |
|
|
|
|
Ek initial |
Ek final |
blue |
5.0 |
|
|
|
|
|
|
green |
5.0 |
|
|
|
|
|
|
total |
----- |
----- |
----- |
|
|
|
|
Collision 5 e = ____ |
|||||||
Object |
mass |
|
|
|
|
Ek initial |
Ek final |
blue |
5.0 |
|
|
|
|
|
|
green |
5.0 |
|
|
|
|
|
|
total |
----- |
----- |
----- |
|
|
|
|
Conclusion
LAB 2. Answer the following questions using the data collected in the collision tables:
-
Is momentum conserved in each collision?
-
Is kinetic energy conserved in each collision?
1.13. Page 4
Module 2—The Conservation of Momentum in Isolated Systems
The Difference Between Elastic and Inelastic Collisions
In a collision, momentum is always conserved, but kinetic energy is not. Sometimes, the kinetic energy is nearly conserved. In other collisions, it is hardly conserved at all. What is going on?
During a collision, energy changes form. As objects interact and collide, they change shape and are distorted. When this occurs, the kinetic energy of the colliding bodies is converted into potential energy, or dissipated as sound or heat. The extent to which the initial kinetic energy is converted to final kinetic energy during the collision determines the elasticity of the collision.
There is a spectrum of elasticity: collisions can range from being perfectly elastic to perfectly inelastic. As collisions become more and more inelastic, more and more kinetic energy is lost.
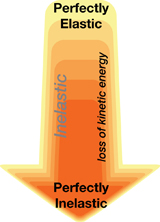
Perfectly Elastic Collisions
In a perfectly elastic collision, the total kinetic energy of the system is conserved. Perfectly elastic collisions generally occur only at the subatomic level.
Inelastic Collisions
In an inelastic collision, some kinetic energy is lost, generally as sound or thermal energy. This is a broad range and most collisions fall within this class.
Perfectly Inelastic Collisions
In a perfectly inelastic collision (also called completely inelastic), the colliding objects stick together upon impact. There is the greatest loss of kinetic energy in this type of collision.
 Self-Check
Self-Check
SC 2. Imagine throwing a perfectly spherical bouncy, elastic ball against the wall.
- Describe the shape of the ball before, during, and after the collision.
before: _______ during: __________ after: __________
- Describe what happens to the kinetic energy of the ball during the interaction. Is the kinetic energy of the ball conserved? If not, what happened to it?
SC 3. Imagine throwing a blob of playdough against the wall.
- Describe the shape of the blob before, during, and after the collision.
before: _________during: _____________ after: ____________
- Describe what happens to the kinetic energy of the blob during the interaction. Is the kinetic energy of the blob conserved? If not, what happened to it?
 Self-Check Answers
Self-Check Answers
SC 2.
-
before: spherical during: squished after: spherical
-
The kinetic energy of the ball is nearly conserved, with some kinetic energy being used as work done to momentarily change the shape of the ball.
SC 3.
-
before: blob during: flat after: stays flat
-
The kinetic energy of the playdough is not conserved. Most of the kinetic energy is used in order to change the shape of the playdough permanently.
The Coefficient of Restitution Defines Elasticity
Is there a range of elasticity in the collisions that were performed in the lab? Recall that in each collision, a value known as e was recorded at the top of each table. Now we will examine what the e value represents. Use the lab data tables to complete the Module 2: Lesson 2 Assignment.
 Module 2: Lesson 2 Assignment
Module 2: Lesson 2 Assignment
Remember to submit the answers to A 1 and A 2 to your teacher as part of your Module 2: Lesson 2 Assignment.
A 1. Complete the data table below by doing the following:
a. Record the total ![]() , total
, total ![]() , and e for each collision from the lab data tables.
, and e for each collision from the lab data tables.
b. Calculate the percentage of loss in kinetic energy for each collision using:
![]()
| Collision | e |
Total Ek Initial |
Total Ek Final |
Loss in Ek (%) |
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
A 2. Using the same data table above, compare the percentage of total kinetic energy lost during each collision to the value of e; e is called the elasticity of the collision. What is the relationship between the percentage of loss in kinetic energy and e?
1.14. Page 5
Module 2—The Conservation of Momentum in Isolated Systems
 Read
Read
Read “Inelastic Collisions” on page 483 of your physics textbook. Continue by studying “Example 9.10” on pages 484 and 485 of your textbook.
 Self-Check
Self-Check
SC 4. Answer “Practice Problem 1” on page 484 of your textbook.
 Self-Check Answers
Self-Check Answers
SC 4.
Given
![]() mp = 1.00 kg
mp = 1.00 kg ![]()
Required
The velocity of the bullet just before impact, ![]() .
.
Analysis and Solution
Choose the system of bullet and pendulum as an isolated system. Since the pendulum is stationary before the bullet hits, its initial velocity is zero; thus, its initial momentum ![]() . After the collision, the bullet and pendulum move together as a unit. The kinetic energy of the pendulum-bullet system is converted into gravitational potential energy:
. After the collision, the bullet and pendulum move together as a unit. The kinetic energy of the pendulum-bullet system is converted into gravitational potential energy:
Ek = Ep
Apply the law of conservation of energy to find the speed of the pendulum-bullet system just after impact:
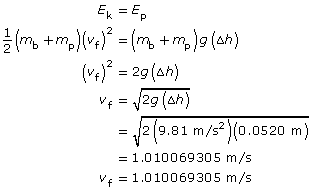
Apply the law of conservation of momentum to find the initial velocity of the bullet:
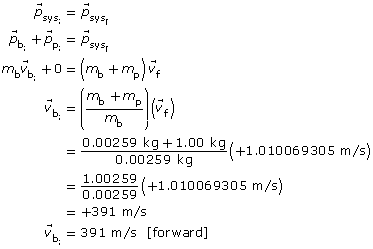
Paraphrase
The initial velocity of the bullet immediately before impact was 391 m/s [forward].
 Read
Read
Study “Example 9.11” on page 485 of your textbook.
 Self-Check
Self-Check
SC 5. Answer “Practice Problem 1” on page 485 of your textbook.
 Self-Check Answers
Self-Check Answers
SC 5.
Given
mass of dart md = 0.012 kg
mass of block-glider mb = 0.200 kg
final velocity of system ![]()
initial velocity of dart ![]()
Required
The amount of kinetic energy lost immediately after the interaction.
Analysis and Solution
the initial energy of the system comes from the kinetic energy of the dart:
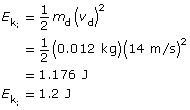
The final kinetic energy comes from the dart-block-glider system.
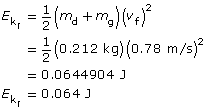
The difference between the initial and final kinetic energies is the kinetic energy lost.
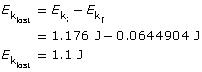
Paraphrase
There was 1.1 J lost immediately after the interaction of the dart and the block-glider system.
 Try This
Try This
TR 1. Answer “Practice Problem 2” on page 484 of your textbook.
TR 2. Answer “Practice Problem 2” on page 485 of your textbook.
 Module 2: Lesson 2 Assignment
Module 2: Lesson 2 Assignment
Remember to submit the answers to A 3 to your teacher as part of your Module 2: Lesson 2 Assignment.
A 3. Design an experiment that would let you answer the following problem:
Is the collision between a ball pendulum and a block pendulum elastic, inelastic, or completely inelastic?
The following four diagrams give you a starting point for your experiment.
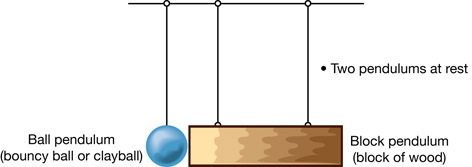
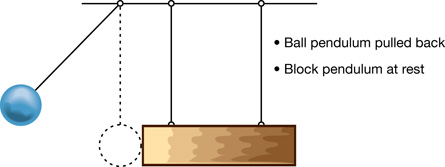
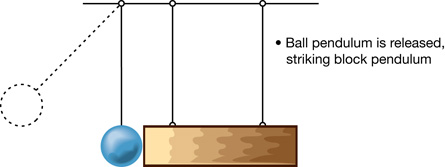
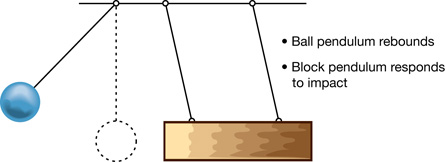
From “Examples 9.10” and “9.11” of your textbook, you will be familiar with using gravitational potential energy to find the kinetic energy of a ball pendulum. You can deal with the kinetic energy of the block pendulum in a similar fashion.
You need to present the following in your experimental design:
-
the measurements that need to be taken
-
the calculations that would have to be made
-
the criteria you would use to answer the problem
1.15. Page 6
Module 2—The Conservation of Momentum in Isolated Systems
 Reflect and Connect
Reflect and Connect

© Aleksandar Kamasi/shutterstock
In the Get Focused section of this lesson, you were asked this question: in a collision between two automobiles, is it better for the occupants if the collision is elastic or inelastic?
Now that you know the differences between elastic and inelastic collisions, you should be ready to complete the necessary analysis to answer this question. A good place to begin is the collision between the ball pendulum and the block pendulum for which you designed an experiment in A 3.
In one version of this experiment, a bouncy ball attached to a long string collides with a wooden block that is also suspended by a long string. In other words, a bouncy-ball pendulum collides with a wooden-block pendulum. Before the collision, the bouncy ball has all the kinetic energy because the wooden block is at rest. After the collision, both objects have some kinetic energy.
The following diagram summarizes typical results:

In another version of this experiment, the bouncy ball is replaced with a ball of clay. Before the collision, the ball of clay has all the kinetic energy because the block of wood is at rest. After the collision, both objects have some kinetic energy. The following diagram summarizes typical results:

The results for the pendulum experiment illustrate how the properties of the materials impact the transfer of kinetic energy in a collision. Some of the initial kinetic energy was used to do work to change the shape of the clay ball, so there was less kinetic energy available for the objects after the collision.

© felix casio/shutterstock
An automobile collision is more like the collision between the clay ball and the block than the bouncy ball and the block. Some of the initial kinetic energy is used to do work to change the shape of the crumple zones of the vehicle. The amount of kinetic energy transferred from one vehicle to the other depends upon the amount of work that is done to change the shape of the vehicles. Although this energy transfer has nothing to do with impulse, the resulting impulse that acts on each vehicle in a collision is strongly influenced by how the transfer of kinetic energy occurs between the two vehicles. You can see why by returning to typical data from the experiments of the two pendulums.
In the case of the bouncy ball and the wooden block, typical data for the collision is shown in the following diagram:
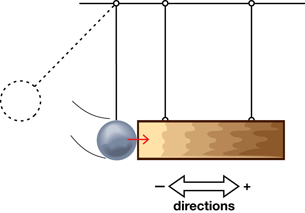
bouncy ball
|
← Before the collision →
← After the collision → |
wooden block
|
Determine the impulse that acted on the bouncy ball:
|
Determine the impulse that acted on the wooden block:
|
As you can see, the impulse for each has the same magnitude but opposite direction.
When a clay ball collides with a wooden block, the velocity values are significantly reduced due to the lower values of kinetic energy. The following diagram shows typical results:

clay ball
|
← Before the collision →
← After the collision → |
wooden block
|
Determine the impulse that acted on the clay ball:
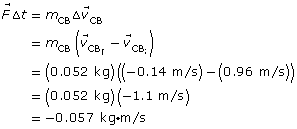
Determine the impulse that acted on the wooden block:
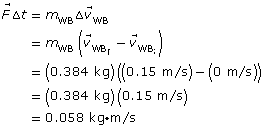
 Self-Check
Self-Check
SC 6. Explain why it would be better to be in a vehicle that is in an inelastic collision with another object rather than a vehicle in an elastic collision with another object.
 Self-Check Answers
Self-Check Answers
SC 6. Inelastic collisions involve a significant reduction in the kinetic energy of the objects after the collision since very little bouncing or reversal of direction occurs. This means that the overall change in velocity is less, so the change in momentum is less. Therefore, less impulse is required to cause that change in momentum. In addition, the time interval for the inelastic collision is increased because crumpling takes time. As was mentioned in the previous module, if the time interval for an interaction lengthens, then the force required reduces to achieve the same impulse.
 Reflect on the Big Picture
Reflect on the Big Picture

© Katherine Welles/shutterstock
Recall the collision of Kathy and Bill in the Big Picture section. Based on the information in this lesson, you can add to your Module 2 Project.
Using the principle of conservation of momentum the police determined that Bill’s truck was travelling at 2.3 m/s before the collision, and Kathy’s car was travelling at 15 m/s before the collision.
Add the answers to the following questions to the document titled “Crash Analysis” that you started in Lesson 1:
- What is the kinetic energy of the vehicles before and after the collision? (Analytic)
- Is kinetic energy conserved? If kinetic energy is not conserved, what does this tell us about the type of collision? (Holistic)
Scoring Guide for Analytic Questions
Scoring Guide for Holistic Questions
Remember to re-save your updated document in your Physics 30 course folder. You will submit the Module 2 Project to your teacher for marks when you have completed the module.
 Module 2: Lesson 2 Assignment
Module 2: Lesson 2 Assignment
Remember to submit the Module 2: Lesson 2 Assignment to your teacher.
1.16. Page 7
Module 2—The Conservation of Momentum in Isolated Systems
 Lesson Summary
Lesson Summary
At the start of this lesson, you were asked the following essential questions:
-
How can the kinetic energy of the objects in a system before and after a collision be used to categorize the type of collision?
-
What is the fundamental difference between an elastic and an inelastic collision?
-
In a collision between two automobiles, is it better for the occupants if the collision is elastic or inelastic?
The kinetic energy values of all the objects in a system can be used to categorize a collision as elastic, inelastic, or perfectly (completely) inelastic. In the case of elastic collisions, the total kinetic energy of the system before the collision equals the total of the kinetic energy of the system after the collision. In other words, kinetic energy is conserved. These collisions are rare with regard to the collision of everyday objects because some of the kinetic energy is usually converted to sound, thermal energy, or deformation. This is the fundamental difference between an elastic collision and an inelastic collision.
In an inelastic collision, the total kinetic energy of the system after the collision is less than the total kinetic energy of the system before the collision. In other words, kinetic energy is not conserved. In some cases, the kinetic energy is completely converted to other forms of energy after the collision. In these cases, the collision is described as being perfectly, or completely, inelastic.
In collisions between two automobiles, it is better for the occupants if the collision is inelastic rather than elastic. Crumple zones of vehicles are designed to transform some of the initial kinetic energy into work. This work changes the shapes of crushable parts of the vehicle. Since the vehicles have less kinetic energy after the collision, there tends to be less reversal of direction. The change in velocity of each vehicle is less, so the change in momentum for each vehicle is less. Thus, the impulse acting on each vehicle is reduced. Since inelastic collisions between vehicles involve the crumpling of crushable parts, the time interval for the interaction is increased, which reduces the forces acting on each vehicle.
1.17. Lesson 3
Module 2—The Conservation of Momentum in Isolated Systems
Lesson 3—Analyzing Non-Linear Collisions
 Get Focused
Get Focused

© cindy xiao/shutterstock
Intersections are busy places. So busy that, despite traffic lights, signs, markings, and warnings, vehicles still collide. In the previous lesson the rear-end collision was explored in the context of a linear collision. These types of collisions are common at intersections where vehicles moving in the same direction have to stop periodically. But what happens when vehicles travelling at right angles to one another collide, as in the Module 2 project with Kathy and Bill? What happens to mass, velocity, and momentum in a non-linear interaction, such as a T-bone collision?
In this lesson you will apply the law of conservation of momentum and component analysis to analyze non-linear collisions, such as that of Bill and Kathy in the Big Picture.
You will explore collisions of this nature in the context of the following questions:
-
Is momentum conserved in a non-linear collision?
-
How is component analysis applied to solve non-linear collision problems?
-
Can it be proven, beyond a reasonable doubt, that Kathy was moving at the speed limit just prior to the collision described in the accident scenario in the Big Picture?
 Module 2: Lesson 3 Assignments
Module 2: Lesson 3 Assignments
Your teacher-marked Module 2: Lesson 3 Assignment requires you to submit a response to the following:
-
Assignment—A 1, A 2, A 3, and A 4
Remember that these questions provide you with the practice and feedback that you need to successfully complete this course. You should respond to all the questions and place those answers in your course folder.
You will also complete your Module 2 Project that you started in the previous lessons and saved to your course folder. The finished project will be submitted to your teacher for marks once you have completed Module 2.
1.18. Page 2
Module 2—The Conservation of Momentum in Isolated Systems
 Explore
Explore
What is the difference between a linear and non-linear interaction? To view an example of a non-linear collision, watch this animation.
Is Momentum Conserved in a Non-linear Collision?
In the previous lesson you learned about momentum and the law of conservation of momentum in the context of one-dimensional collisions: for any isolated system, the total momentum does not change. In a collision, momentum is conserved. The total momentum before the collision is equal to the total momentum after the collision.
Is the same true of two-dimensional collisions?
 Watch and Listen
Watch and Listen
If you don’t feel very comfortable with vector analysis, you can choose to open and try this animation titled Component Vector Analysis.
 Module 2: Lesson 3 Assignment
Module 2: Lesson 3 Assignment
Remember to submit the answer to A1 to your teacher as part of your Module 2: Lesson 3 Assignment.
LAB 1. A simulation can be used to determine if momentum is conserved in two-dimensional collisions. Use the Collision 2D simulator to help you answer the following questions.
Once the simulation is open, follow these steps:
-
Toggle “Show CM” and “Show CM Frame” to the off position (
 ).
). -
Leave the “Show Trails” box checked.
-
Move the “Impact Parameter” slider to a value other than zero.
-
Press “Play” and observe the collision.
-
Press “Pause” before either of the objects leaves the viewing area.
-
Press the “Data” button to display the data describing the collision.
Perform one two-dimensional collision; then complete the following table. To generate a new collision, press the “New” button (![]() ) and move the Impact Parameter slider to any value other than zero. Press the “Data” button (
) and move the Impact Parameter slider to any value other than zero. Press the “Data” button (![]() ) to view the collision information that is required to complete the following table.
) to view the collision information that is required to complete the following table.
Collision 1 (sample data) |
|||||||
Object |
Mass |
|
|
|
|
|
|
blue |
|
|
|
|
|
|
|
green |
|
|
|
|
|
|
|
-
How would you calculate the total momentum before and after a two-dimensional collision?
-
Would the same analysis that you used for one-dimensional situations work here?
-
According to your observations, is momentum conserved in a two-dimensional collision?
According to the data you collected for LAB 1 and using the typical analysis performed for a one-dimensional collision, you should have found that momentum in a two-dimensional collision is not conserved. However, this is contrary to the law of conservation of momentum, which means a new type of analysis must be used for two-dimensional collisions.
This new type of analysis is based on the following principles, which apply to two-dimensional interactions:
-
Momentum in the x direction is conserved.
-
Momentum in the y direction is conserved.
 Try This
Try This
TR 1. With the following data from the simulation, carry out a calculation of the total momentum before and after the collision using the analysis method that was just introduced to you.
Object |
Mass (kg) |
|
|
||
Magnitude |
Direction |
Magnitude (m/s) |
Direction |
||
blue ball |
5.00 |
8.00 |
0 |
2.80 |
69.51 |
green ball |
5.00 |
0.0 |
0 |
7.50 |
−20.49 |
- What is the initial total momentum in the x direction?
- What is the initial total momentum in the y direction?
- What is the final total momentum in the x direction?
- What is the final total momentum in the y direction?
On the next page is an example of how to describe vectors (such as momentum) using components and how to apply the law of conservation of momentum correctly to a two-dimensional collision. You may wish to look at the vector review in Module 1 if you’re feeling a bit rusty on vector analysis.
1.19. Page 3
Module 2—The Conservation of Momentum in Isolated Systems
Describing Momentum Using Vector Components
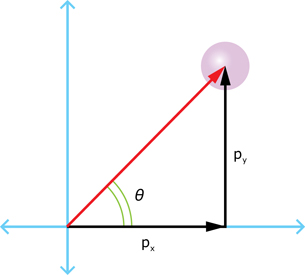
Any two-dimensional vector, such as momentum, can be resolved into components. Generally, we resolve vectors into horizontal (x) and vertical (y) components. The diagram to the right shows a vector, ![]() , resolved into its x and y components. Using this diagram and some basic trigonometric identities (sin, cos, tan), answer the Self-Check questions below.
, resolved into its x and y components. Using this diagram and some basic trigonometric identities (sin, cos, tan), answer the Self-Check questions below.
 Self-Check
Self-Check
SC 1. What is the expression that gives px as a function of ![]() and θ?
and θ?
SC 2. What is the expression that gives py as a function of ![]() and θ?
and θ?
SC 3. Write a general expression for ![]() , if both px and py are known.
, if both px and py are known.
SC 4. If both px and py are known, what is the general expression for θ?
 Self-Check Answers
Self-Check Answers
SC 1.![]()
SC 2.![]()
SC 3. ![]()
SC 4. ![]()
Analyzing Collisions Using Component Analysis
See this demonstration of adding vectors for a 2-D collision. Applying the law of conservation of momentum in two-dimensional collisions is more complex than that of a one-dimensional collision. Essentially, the law of conservation of momentum is applied twice—once in the x and once in the y directions. Following is an example of how to apply the law of conservation of momentum correctly to solve two-dimensional collision problems.
Example Problem
An 8.0-kg mass collides elastically with a 5.0-kg mass that is at rest. Initially, the 8.0-kg mass was travelling to the right at 4.5 m/s. After the collision, it is moving with a speed of 3.65 m/s and at an angle of 27° to its original direction.
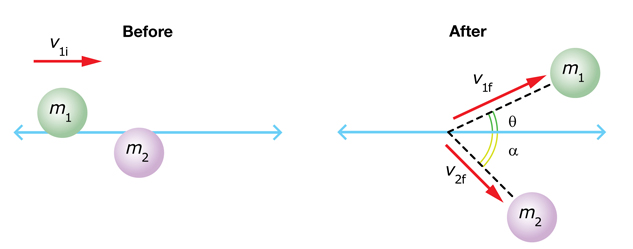
What is the final velocity for the 5.0-kg mass?
Example Solution
Given
mass 1 m1 = 8.0 kg
initial velocity of mass 1 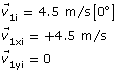
final velocity of mass 1 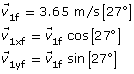
mass 2 m2 = 5.0 kg
initial velocity of mass 2 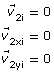
Required
The final velocity of mass 2, ![]() .
.
Analysis and Solution
Initially, mass 1 moves to the right, and mass 2 is at rest. Thus, the total momentum is in the x direction (to the right). After the collision, mass 1 travels at an angle of 27° to its original direction of motion; it now has momentum in the y direction as well as the x direction. For momentum to be conserved, mass 2 must have momentum in both the x and y directions.
Define motion to the right as positive, which follows the usual convention. As well, measure angles counterclockwise from the horizontal.
Use the law of conservation of momentum to solve this question. Since momentum is conserved in both the x and y directions, we can set up two sets of equations—one each to solve for v2fx and v2fy.
Conservation of momentum in the x direction:
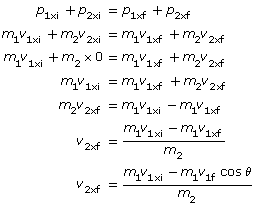
Conservation of momentum in the y direction:
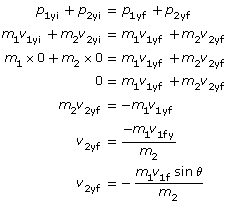
The final velocity for mass 2 in the x direction:
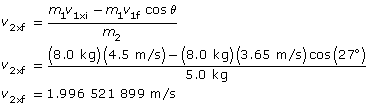
The final velocity for mass 2 in the y direction:
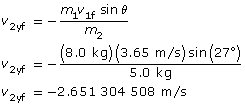
Once you know the final velocity in the x and y directions, you can find the final velocity and direction of motion for mass 2. Remember, do not use the rounded off values in your calculations—use rounded numbers for the final paraphrase.
Final velocity for mass 2:
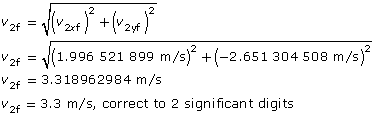
Direction of motion:
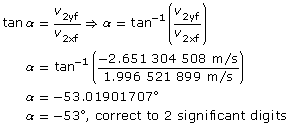
This answer seems to make sense—mass 2 has to move to the right and down in order to conserve momentum. Furthermore, this answer can be verified with the simulation. Check it yourself!
Paraphrase
The final velocity of mass 2 is 3.3 m/s [−53°] or 3.3 m/s [307°].
 Try This
Try This
TR 2.A 9.0-kg ball is travelling to the right at 8.0 m/s until it impacts a 3.0-kg stationary ball. After the collision, the 9.0-kg ball is travelling at 5.61 m/s at an angle of 7.8º above the horizontal. Calculate the velocity of the 3.0-kg ball after the impact. (Note: To view and verify this collision using the simulation, open the “Options” (![]() ) and set e = 0.44. Then set the blue mass to 9.0 kg and the green mass to 3.0 kg.)
) and set e = 0.44. Then set the blue mass to 9.0 kg and the green mass to 3.0 kg.)
 Read
Read
Read “Collisions in Two Dimensions” on pages 487 to example 9.14 on page 495 of your physics textbook.
 Module 2: Lesson 3 Assignment
Module 2: Lesson 3 Assignment
Remember to submit the answers to A 1 and A 2 to your teacher as part of your Module 2: Lesson 3 Assignment.
A1. A car with a mass of 1400 kg is westbound at 50 km/h. It collides at an intersection with a northbound truck having a mass of 2000 kg and travelling at 40 km/h. What is the initial common velocity of the car and truck immediately after the collision if they have an inelastic collision?
A2. A police car with a mass of 1460 kg is headed west at 60 km/h when it has an inelastic collision with a southbound 2000-kg ambulance. The wreckage ended up travelling at 45 km/h at 236°. What was the initial speed of the ambulance?
 Read
Read
Read “Elastic and Inelastic Collision in Two Dimensions” on pages 495 to 498 of your physics textbook.
 Try This
Try This
TR 3. Answer questions 1 to 4 in “9.4 Check and Reflect” on page 499 of your physics textbook.
 Module 2: Lesson 3 Assignment
Module 2: Lesson 3 Assignment
Remember to submit the answers to A 3 and A 4 to your teacher as part of your Module 2: Lesson 3 Assignment.
A3. A billiard cue ball with a mass of 0.60 kg and an eight ball with a mass of 0.55 kg are rolled toward each other. The cue ball has a velocity of 3.0 m/s at 360°, and the eight ball has a velocity of 2.0 m/s at 90°. After the collision, the cue ball moves off at a velocity of 2.0 m/s at 40°.
- What is the velocity of the eight ball?
- Prove whether or not the collision is elastic.
A4. A proton with an initial velocity of 2800 m/s [90°] is struck by a neutron heading at 320° with a speed of 2900 m/s. The neutron bounces off of the proton with a velocity of 1864 m/s [270°].
- What is the final velocity of the proton?
- Prove whether or not the collision is elastic.
1.20. Page 4
Module 2—The Conservation of Momentum in Isolated Systems
 Reflect and Connect
Reflect and Connect

Maps courtesy of ERCB/AGS
The Alberta Traffic Safety Plan reports the following statistics:
-
A traffic collision occurs every five minutes in Alberta.
-
On average, one person is killed and 65 injured in collisions every day.
-
Collisions kill six times as many people as homicide, eight times as many as AIDS, and 100 times as many as meningitis.
-
The costs associated with collisions in Alberta are $12 million per day, or more than $4 billion per year.
The statistics indicate that collisions are common and have significant costs both to property and people.
An intersection is essentially a planned point of conflict. Two roads, travelling in different directions, meet with drivers travelling in a variety of directions. The greater the number of points of conflict, the greater the number of collisions.
To understand the scope of this problem, open an online map site that allows a satellite view. Then find your house. Use the satellite view, and zoom in as far as you can with a clear satellite image. How many intersections are in your neighbourhood? Now find the intersection of 75th street NW and 98th Avenue NW in Edmonton by entering the address in the search area. Zoom out and look at more of the city. How many intersections do you think there are? Now try the intersection of 17th Avenue SW and 14th Street SW in Calgary. In cities such as Edmonton and Calgary, there are many intersections.
Maps courtesy of ERCB/AGS
 Reflect on the Big Picture
Reflect on the Big Picture

© Katherine Welles/shutterstock
Recall the collision of Kathy and Bill in the Big Picture section. Based on what you learned in this lesson, continue to analyze this collision.
Complete your Module 2 Project. Add the following questions and answers to your Crash Analysis stored in your Physics 30 course folder.
In previous lessons you determined the magnitude of the momentum of the combined vehicles just after impact and the kinetic energy before and after the impact. The following vector diagram illustrates the direction of the momentum vector based on evidence from the scene.
The two momentum vectors before the collisions are represented in blue. The momentum after the collision is in red. Adding the two momentum vectors before the collision equals the momentum after the collision, according to the law of conservation of momentum.
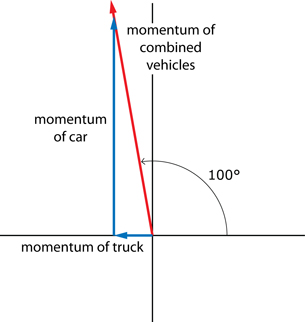
While the photo suggests a much more complex collision than the given diagram, assume that the diagram shows exactly what happened.
-
Using this vector diagram and your calculated value for the momentum of the combined vehicles, verify the police calculations and determine the momentum and velocity of Bill’s truck just before the collision. (Analytic)
-
Using this vector diagram and your calculated value for the momentum of the combined vehicles, verify the police calculations and determine the momentum and velocity of Kathy’s car just before the collision. (Analytic)
-
Does your analysis prove, beyond a reasonable doubt, that Kathy was, in fact, travelling at the speed limit of 50 km/h just prior to the accident? What assumptions did you make in your solution to determine this? (Holistic)
Before submitting your answers for your Module 2 Project double check your answers with the following rubrics:
Scoring Guide for Analytic Questions
Scoring Guide for Holistic Questions
Answering these questions completes your Module 2 Project. Submit your Crash Analysis to your teacher for marks.
 Module 2: Lesson 3 Assignment
Module 2: Lesson 3 Assignment
Remember to submit the following to your teacher:
- Module 2: Lesson 3 Assignment
- Module 2 Project
1.21. Page 5
Module 2—The Conservation of Momentum in Isolated Systems
 Lesson Summary
Lesson Summary
At the start of this lesson, you were asked the following essential questions:
-
Is momentum conserved in a non-linear collision?
-
How is component analysis applied to solve non-linear collision problems?
-
Can it be proven, beyond a reasonable doubt, that Kathy was moving at the speed limit just prior to the collision described in the accident scenario in the Big Picture?
You looked at collisions that occur in two dimensions. You verified that the total momentum of a system is conserved during a collision. Specifically, the total momentum of the x direction and the y direction is also conserved during a collision. The key principles are as follows:
-
Momentum is a vector and can be resolved into components.
-
During a collision, the total momentum of the components is conserved:
![]() and
and ![]()
Using this conservation principle, it is possible to analyze two-dimensional collisions, such as those of vehicles that meet in an intersection.
1.22. Module Summary/Assessment
Module 2—The Conservation of Momentum in Isolated Systems
 Module Summary
Module Summary
In Lesson 1 you investigated the momentum in an isolated system during a collision. You verified one of the fundamental laws that govern physical processes, the law of conservation of momentum. In summary, the law states: momentum is “mass in motion" or a measure of how much motion an object has. Expressed as an equation, it is as follows:
![]()
In a collision between two objects, the change in momentum of one object is equal and opposite to the change in momentum of the other object. Expressed as an equation, it is as follows:
![]()
The law of conservation of momentum states that the sum of the momentum in a system before a collision equals the sum of the momentum in the same system after a collision. Expressed as an equation, it is as follows:
![]()
You learned that we can analyze collisions to determine initial velocities or predict final velocities by applying the conservation of momentum.
In Lesson 2 you investigated the total kinetic energy of a system before and after a collision and found that kinetic energy is not always conserved. This is a criterion that distinguishes between two types of collisions. Furthermore, the amount of lost kinetic energy can be used to produce a spectrum of “elasticity,” including the following three generalizations for collisions:
-
Perfectly elastic collisions result in the total kinetic energy of the system being conserved. Perfectly elastic collisions generally occur only at the subatomic level.
-
Inelastic collisions involve some loss of kinetic energy, generally as sound or thermal energy. This is a broad range, and most collisions fall within this class.
-
Perfectly inelastic collisions are ones in which the colliding objects stick together upon impact. There is the greatest loss of kinetic energy in this type of collision.
All linear and non-linear collisions are described by one of these three general classifications, including the one analyzed for the module assessment in the form of a crash reconstruction analysis.
In Lesson 3 you studied collisions that occur in two dimensions. You verified that the total momentum of an isolated system is conserved during a collision. Specifically, the total momentum in the x direction and in the y direction is also conserved during a collision.
Therefore, ![]() and
and ![]() .
.
Using this conservation principle, it is possible to analyze two-dimensional collisions, such as those of vehicles that meet in an intersection.
Module Assessment
Module 2 Project
In each lesson you have been working on a crash analysis of the collision between Kathy and Bill. The last part of the analysis was completed at the end of Lesson 3. Submit the entire analysis including answers to all of the questions in the Reflect on the Big Picture sections of Lessons 1, 2, and 3 of Module 2.
1.23. Module Glossary
Module 1—Momentum and Impulse
Module Glossary
momentum: the product of the mass and velocity of an object