Module 7
| Site: | MoodleHUB.ca 🍁 |
| Course: | Physics 30 SS |
| Book: | Module 7 |
| Printed by: | Guest user |
| Date: | Wednesday, 17 December 2025, 2:43 AM |
Description
Created by IMSreader
1. Module 7
Module 7—Investigating the Nature of the Atom
Module Introduction
In this module you will explore the early investigations related to the structure of matter. From investigations with cathode rays to the interaction of electromagnetic radiation and matter, these early experiments laid the foundation for our current understanding of the structure of matter.
The discovery of the electron and nucleus, as well as their physical characteristics, was critical to building an understanding of how the atom is modelled and organized. At the end of Module 7 you will understand the electrical nature of the atom and the quantization of energy in the atom and nucleus.
Specifically, you will be asked to apply your knowledge to answer the following question:
- How does the quantization of energy in atoms and nuclei reveal the electrical nature of the atom?
1.1. Big Picture
Module 7—Investigating the Nature of the Atom
 Big Picture
Big Picture
© James Thew/shutterstock
In this artistic representation of the atom, you can see smaller particles orbiting along what appear to be circular paths that enclose a chunky nucleus made up of many smaller particles. Is this really what an atom looks like? Perhaps a better question would be this: Can an atom even be seen? If it could be seen, what would it look like?
Logically, the last question may seem pointless if the answer to the one before it is no.
What is more important, however, is that you understand how the atom is organized so you can predict how it will interact with its environment. And since the atom is too small to see or interact with, a model is used to help bring meaning to the physical reality. Scientists have been working with models of the atom for some time, probing its internal structure and electrical nature. This work has led to the ongoing development of valuable technologies, such as the mass spectrometer, which can identify unknown atoms and elements based on charge and mass.
By the end of Module 7 you will understand how current models of the atom can be applied in technologies used to explore the chemistry of the Earth, the Sun, and other planets in our solar system. You will also see how the practice of science plays out within the social context of the scientific community. You will investigate the nature of the atom.
As you are working in Module 7, keep the following questions in mind:
- How did the cathode ray contribute to the development of atomic models?
- How did J. J. Thomson determine the charge-to-mass ratio of an electron?
- How did Millikan discover the charge of an electron and how did this elementary charge inform models of the atom?
- What did Rutherford’s scattering experiment suggest about the nature of the nucleus? How did it lead to the planetary model of the atom?
- What is the Bohr model of the atom? How are the concepts of stationary states and energy quantization used to explain how a gas absorbs and emits only certain wavelengths of electromagnetic radiation?
Module Assessment
Each lesson has a teacher-marked assignment, based on work completed in the lesson. In addition, you will be graded on your contributions to the Discuss section of each lesson.
You will also be asked to complete Self-Check or Try This questions, which you should place in your Physics 30 course folder. These are not formally assessed, but they are a valuable way to practise the concepts and skills of the lesson. These activities can provide you with reflective feedback on your understanding of the lesson work.
You will be marked for your lesson work on the following items:
- Module 7: Lesson 1 Assignment
- Module 7: Lesson 2 Assignment
- Module 7: Lesson 3 Assignment
At the end of the module you will complete a module assessment that consists of two Diploma Exam-style written-response questions. The first question will assess your knowledge of charge-to-mass ratios and the second question will assess your knowledge of electromagnetic induction. See the Module Summay and Assessment page for more information.
1.2. In this Module
Module 7—Investigating the Nature of the Atom
In This Module
Lesson 1—Cathode Rays and Thompson’s Experiment
In this lesson you will learn about the discovery of the electron and its charge-to-mass ratio. You will explore early experiments with cathode ray tubes and the applications of such technologies in modern mass spectrometers.
You will investigate the following essential questions:
-
How did the cathode ray contribute to the development of atomic models?
-
How did J. J. Thomson determine the charge-to-mass ratio of an electron?
-
How did Thomson’s experiment contribute to science and technology?
Lesson 2—The Millikan Experiment
In this lesson you will learn about Millikan’s oil drop experiment and how he determined the elementary charge of an electron using scientific judgment.
You will investigate the following essential questions:
-
How were Millikan’s experimental design and apparatus applied to determine the charge of a single electron?
-
How did the new fundamental quantity, the elementary charge, inform models of the atom?
-
Why did Millikan’s use of scientific judgment cause a controversy among other scientists and scholars?
Lesson 3—The Rutherford and Bohr Models of the Atom
In this lesson you will explore information about the atom revealed by its interaction with electromagnetic radiation and with charged particles.
You will investigate the following essential questions:
-
What does Rutherford’s scattering experiment suggest about the nature of the nucleus, and how did it lead to the planetary model of the atom?
-
What is the Bohr model of the atom? How is the concept of stationary states and energy quantization used to explain how a gas absorbs and emits only certain wavelengths of electromagnetic radiation?
1.3. Lesson 1
Module 7—Investigating the Nature of the Atom
Lesson 1—Cathode Rays and Thomson’s Experiment
 Get Focused
Get Focused

Spacescapes/Getty Images
Scientists believe that Earth’s early atmosphere was similar to the atmosphere that currently exists on Saturn’s moon Titan. Presumably, this could give rise to conditions that may support life on Titan. It is a unique moon—the only one known to have a fully developed atmosphere with more than just trace gases.
In fact, the atmosphere is so thick and the gravity so low that you could fly through it by flapping wings attached to your arms! It is 98.4% nitrogen and 1.6% methane, and it appears as thick orange smog due to reactions caused by ultraviolet radiation and methane in the upper atmosphere. How is it possible to know such complex details about a place that can’t even be seen with the naked eye?
The European Space Agency, in conjunction with NASA and the Italian Space Agency, successfully landed the Huygens probe on the surface of Titan on January 14, 2005. The proble had enough power to function during its two and one-half hour descent to the surface and for more than 90 minutes while on the surface. During that time the probe used a mass spectrometer to measure the molecular mass of the gases in the atmosphere and then sent that data back to Earth for analysis.
The molecular mass data from the probe was used to identify and confirm the type of chemicals that make up the moon’s atmosphere. Ironically, this snapshot of data, collected halfway across the solar system, was made possible by the very close examination of the infinitely small. To be precise, the mass spectrometer is a technology that was born from a similar quest for information, a quest that focused on the composition of matter and, in particular, the discovery of the electron. Approximately 105 years before the Huygens probe touched down on Titan, the electron and its characteristics were about to be discovered using similar technology.
In Lesson 1 you will learn about the discovery of the electron and its charge-to-mass ratio. You will explore early experiments with cathode ray tubes and the applications of such technologies in modern mass spectrometers.
In this lesson you will answer the following essential questions:
- How did the cathode ray contribute to the development of atomic models?
- How did J. J. Thomson determine the charge-to-mass ratio of an electron?
- How did Thomson’s experiment contribute to science and technology?
 Module 7: Lesson 1 Assignment
Module 7: Lesson 1 Assignment
Your teacher-marked Module 7: Lesson 1 Assignment requires you to submit responses to the following questions:
- Assignment—A 1, A 2, A 3, A 4, A 5, A 6, and A 7
- Reflect and Connect—RC 1
The other questions in this lesson are not marked by the teacher; however, you should still answer these questions. The Self-Check and Try This questions are placed in this lesson to help you review important information and build key concepts that may be applied in future lessons.
After a discussion with your teacher, you must decide what to do with the questions that are not part of your assignment. For example, you may decide to submit to your teacher the responses to Try This questions that are not marked. You should record the answers to all the questions in this lesson and place those answers in your course folder.
1.4. Page 2
Module 7—Investigating the Nature of the Atom
 Explore
Explore
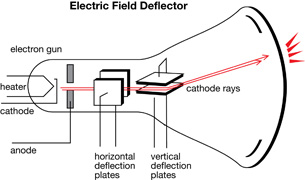
Cathode Rays
All the technology needed to find the electron was available near the end of the 19th century. The manufacturing of sealed glass instruments and tubes had reached a quality that could support low-pressure environments with the operation of a vacuum pump. Around 1850 Heinrich Geissler invented a pump that could produce extremely low pressures. He shaped glass into a tube and evacuated the air from within. Then he filled the tube with a low-density, pure gas. When a potential difference was applied to the electrodes at either end of the tube, a colourful electrical discharge was produced. Further observations indicated that different types of gas emitted a unique and characteristic colour. Geissler called these tubes gas discharge tubes.
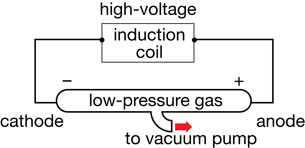
cathode ray: a free electron emitted by a negative electrode in a low-pressure environment
This diagram is an illustration of a simple gas discharge tube.
Immediately, the cathode ray became the subject of intense experimentation.
William Crookes proved that the emissions travelled from the cathode to the anode. For this reason, gas discharge tubes are sometimes called Crookes tubes or, more commonly, cathode ray tubes (CRT). Crookes placed a paddle wheel, which was free to rotate, in the path of the cathode rays.
When the rays hit the paddles, they caused the wheel to move along a track inside the tube. This proved that cathode rays were composed of moving particles that had mass and momentum and were capable of doing work.
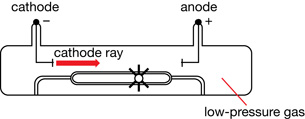
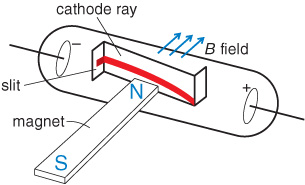
Crookes also demonstrated that cathode rays are deflected by a magnetic field. Using the left-hand rule for moving electric charges in a magnetic field, he proved that the particles were negatively charged and were emitted by the cathode.
Arthur Schuster used a set of external charged plates to demonstrate that the cathode rays were affected by electric fields. The direction of deflection of the cathode rays further proved that they were, in fact, negative.
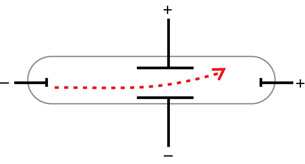
Based on these observations, cathode rays
- travel from the negative electrode to the positive electrode
- travel in straight lines and cause shadows
- have momentum and energy to do work
- are deflected by magnetic and electric fields and have a negative charge
 Read
Read
Read “Cathode-ray Experiments” on pages 754 to 755 of your physics textbook. What was the evidence that the cathode rays were particles with charge and mass?
 Module 7: Lesson 1 Assignment
Module 7: Lesson 1 Assignment
Remember to submit your answer to A 1 to your teacher as part of your Module 7: Lesson 1 Assignment.
A 1. What was the evidence that the cathode rays were particles with charge and mass?
The Thomson Experiment
In 1897 J. J. Thomson attempted to measure both the mass and charge of the negative particles making up the cathode ray. He was unable to measure either the charge or mass by itself, but he was able to measure them both as a ratio. In other words, he designed an experiment to determine the amount of charge per unit of mass for the particles in the cathode ray. The design of his experiment is based on electric and magnetic forces that act on charged particles. Recall the equations and hand rules that describe these forces.
An electrical force can deflect the charged particles in the cathode ray.
![]()
A magnetic force can deflect charged particles in a cathode ray.
![]()

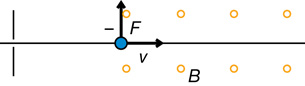
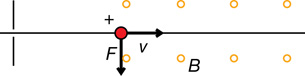
The direction of the force depends on the type of charge and the direction of the electric field. For example,
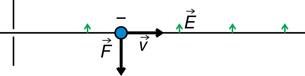
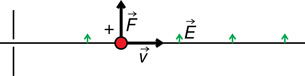
The direction of the force is determined using hand rules. For example,
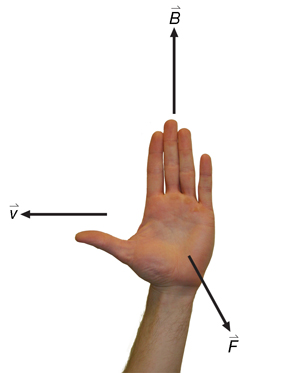
Recall: In the open palm left-hand rule for negative charges, the thumb goes in the direction of movement (![]() ), the fingertips go in the direction of the magnetic field (out of the page in this case), and the palm points in the direction of the force on the charge.
), the fingertips go in the direction of the magnetic field (out of the page in this case), and the palm points in the direction of the force on the charge.
Equation 1
Using only these two forces, Thomson designed an experiment that consisted of two basic investigations. First, he used his apparatus to determine the speed of a cathode ray particle in the tube; then, knowing the speed, he used the apparatus to determine the charge-to-mass ratio of the particle.
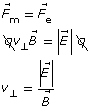
Part 1: Determining the Speed of a Cathode Ray Particle
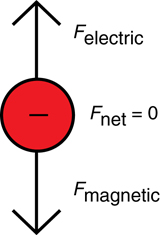
A magnetic field or an electric field acting alone will deflect a charged particle that is travelling perpendicularly to it.
Thomson used this knowledge to determine the speed of a travelling particle using both a magnetic and electric field simultaneously. He set up the apparatus in such a way that the electric force was oriented opposite to the magnetic force. This way, if the magnetic force were equal in magnitude to the electric force, the particle would travel straight through the apparatus. When the particle travels straight through, Equation 1 can be used to calculate its speed.
 Self-Check
Self-Check
SC 1. A beam of electrons is fired to the right into a set of perpendicular electric and magnetic fields. The electric field is oriented downward and the magnetic field is into the page.
- Explain the direction of the electric force acting on the electrons.
- Explain the direction of the magnetic force acting on the electrons.
- If the electrons travel undeflected, draw a free-body diagram of the electrons.
SC 2. A particle travels undeflected (straight) through a Thomson apparatus that has a magnetic field of 2.0 T and an electric field of 100 V/m oriented perpendicularly to one another. Use Equation 1 to determine how fast it is travelling. Show your work and use the Thomson’s Charge/Mass Measurement simulation to verify your answer by setting the calculated velocity, magnetic field, and electric field as stated. You should observe that the particle travels undeflected through the apparatus if your velocity calculation is correct. Note that the applet will take a few minutes to load.
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 1.
- The direction of the electric field is the direction in which a positive particle is pushed; therefore, in a downward field, the negatively charged electron will go the opposite direction, upward.
- Using the left hand rule for negatively charged particles in magnetic fields, the current is travelling to the right (thumb), the magnetic field is into the page (fingers) and the force on the particle is upward (palm faces up).
- Since the electrons are undeflected, the forces—electrical force downward and magnetic force upward—are the same magnitude. The force of gravity is insignificant on such a small particle compared to the other forces, so it is ignored.
SC 2.
Given
![]()
Required
the velocity of the undeflected particle
Analysis and Solution
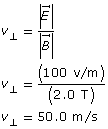
Paraphrase
The velocity of the particle is 50 m/s.
1.5. Page 3
Module 7—Investigating the Nature of the Atom
 Watch and Listen
Watch and Listen
Open Determining Charge-to-Mass Ratio (Thomson's Charge/Mass Measurement) to see how Thomson used magnetic and electric fields to determine the charge-to-mass ratio of a particle.
 Try This
Try This
SIM 1. Open the Thomson’s Charge/Mass Measurement simulation.
Adjust the speed slider to match your answer from SC 1. ![]()
Note: The applet reset button changes all of the sliders, so you must adjust them all before repeating the experiment. Notice the difference in the electron’s path if you try different speeds. Predict what the path will be if you change the charge or mass of the particle. Verify your prediction by changing the charge and mass.
This arrangement with a crossed (perpendicular) pair of uniform electric and magnetic fields is called a velocity selector. If charged particles with a variety of velocities enter the fields, only those whose velocity is perpendicular to both fields and whose speed satisfies ![]() will continue in a straight line. The set-up is, therefore, able to select charged particles of a given velocity from all other particles by setting the fields to appropriate values. Velocity selectors have an application in mass spectrometers.
will continue in a straight line. The set-up is, therefore, able to select charged particles of a given velocity from all other particles by setting the fields to appropriate values. Velocity selectors have an application in mass spectrometers.
The arrangement can also be used to measure the speed of charged particles. One must adjust the electric and magnetic fields until there is no deflection and then use the equation to solve for the speed. It is important to note that the value of the speed for which there is no deflection depends on neither the charge nor the mass of the particle. Therefore, you can use a velocity selector to measure the speed of charged particles even if you do not know their charge or their mass.
 Read
Read
Read “Charge-to-mass Ratio of the Electron” on page 755 of your physics textbook.
Part 2: Determining the Charge-to-Mass Ratio of a Cathode Ray Particle
Having determined the speed of the particles as they are coming from the source, you now have to perform a second experiment to determine the charge-to-mass ratio. In the second experiment the particles go through the same apparatus, but with one of the fields turned off. In this circumstance one field will deflect the particles because there is no other force from the other field to balance it.
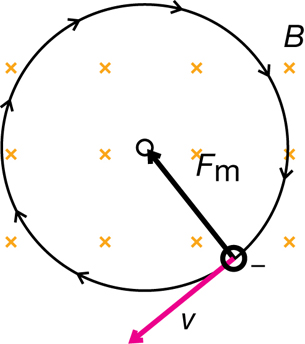
Recall that a magnetic force will produce a perpendicular force on a moving charge as determined by the hand rule. The uniform perpendicular force will cause the charged particle to move along a circular path of constant radius. Therefore,
Finward = Fm
Given the definitions of the inward, centripetal force and the magnetic force, it is possible to derive an equation for the charge-to-mass ratio of the particle exhibiting circular motion in the magnetic field alone.
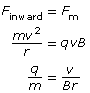
In a Thomson-style experiment, the velocity is first determined using both a known magnetic and electric field. Then, by turning off the electric field and measuring the radius of the circular path made by the charged particles, you would be able to determine the charge-to-mass ratio of the particles.
Thomson determined that the charge-to-mass ratio of the particles in a cathode ray was 1.76 × 1011 C/kg. This value was unique to all cathode rays regardless of the metal electrodes used to produce them. Thomson had discovered the electron, but, more importantly, he had determined that the charge-to-mass ratio for an electron was thousands of times larger than that of a hydrogen ion, which meant that the electron was a “subatomic” particle. He proposed a radical idea at the time—the atom was divisible into smaller particles. And since no positive subatomic particles had been discovered at the time, he suggested that the atom consisted of electrons embedded in a blob of massless positive charge, what is now known as the raisin-bun model of the atom. You will learn more about this model later on in the lesson.
 Read
Read
Read “Determining Charge-to-mass Ratios” on pages 757 to 758 of your physics textbook.
 Self-Check
Self-Check
SC 3. Using the charge and mass values on your physics data sheet, what is the charge-to-mass ratio of
- the proton
- the alpha particle
- the neutron
SC 4. How many times larger is the charge-to-mass ratio of the electron than the proton?
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 3.
- Proton
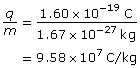
The charge-to-mass ratio of the proton is 9.58×107 C/kg.
- Alpha particle
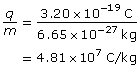
The charge-to-mass ratio of the alpha particle is 4.81×107 C/kg.
- Neutron
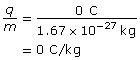
The neutron is neutral, so it has no charge; as a result, the charge-to-mass ratio is zero.
SC 4.
Given
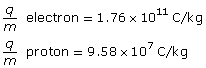
Required
the number of times larger the electron’s charge-to-mass ratio is than the proton’s charge-to-mass ratio
Analysis and Solution
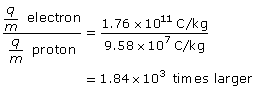
Paraphrase
The charge-to-mass ratio of the electron is 1.84×103 larger.
In order to obtain the charge and mass values on the physics data sheet, experimental data was analyzed. Here are some examples of how that can be done.
Example Problem 1. A charged particle is travelling horizontally at 3.60 × 106 m/s through a vertical magnetic field of 0.710 T. If the radius of the curvature of the particle’s path is 0.950 m, what is the charge-to-mass ratio of the particle?
Given
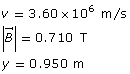
Required
the charge-to-mass ratio of the given particle
Analysis and Solution
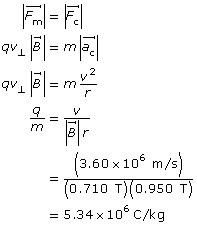
Paraphrase
The charge-to-mass ratio of the particle is 5.34×106 C/kg.
Example Problem 2. What is the speed of an electron that passes through an electric field of 6.30 × 103 N/C and a magnetic field of 7.11 × 10-3 T undeflected? The two fields are perpendicular to each other and to the path of the electron. What is the kinetic energy of the electron?
Given
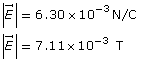
Required
the kinetic energy of the electron
Analysis and Solution
Find the velocity by balancing the force magnetic with the force electric.
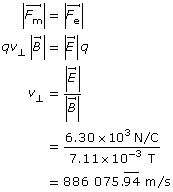
Find the kinetic energy.
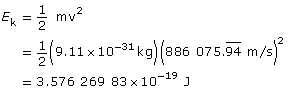
Paraphrase
The kinetic energy of the electron is 3.58×10–19 J.
 Try This
Try This
TR 1. An alpha particle travels through a magnetic field of 0.422 T perpendicular to the field. If the radius of arc of the deflected particle is 1.50 × 10–3 m, what was the speed of the alpha particle? (3.05×104 m/s)
TR 2. A proton travels through a magnetic field at a speed of 5.40 × 105 m/s, perpendicular to the field. If the radius of curvature is 7.20 mm, what is the magnetic field strength? (0.783 T)
TR 3. Alpha particles travel undeflected through magnetic and electric fields that are perpendicular to each other. If the speed of the alpha particles was 7.80 × 105 m/s and the magnetic field strength was 0.220 T, what was the electric field strength? (1.72 × 105 N/C)
 Module 7: Lesson 1 Assignment
Module 7: Lesson 1 Assignment
Remember to submit your answers to A 2, A 3, A 4, and A 5 to your teacher as part of your Module 7: Lesson 1 Assignment.
A 2. What is the charge-to-mass ratio of a particle travelling 3.60 × 105 m/s that is deflected in an arc of radius 7.40 cm as it travels through a magnetic field of 0.610 T?
A 3. Some positively charged particles are found to pass undeflected through perpendicular magnetic and electric fields. The magnetic field strength is 0.650 T, and the electric field strength is 2.10 × 105 N/C. What is the speed of the particles?
A 4. Alpha particles travel through a magnetic field of 0.360 T and are deflected in an arc of 0.0820 m. Assuming the alpha particles are perpendicular to the field, what is the energy of an individual alpha particle?
A 5. Using the charge of an electron (determined by Millikan in another experiment to be 1.60 × 10–19 C and the charge-to-mass ratio of the electron (determined by Thomson to be 1.76 × 1011 C/kg), calculate the mass of an electron.
 Watch and Listen
Watch and Listen
Thomson’s experiment was about more than just finding the electron; it was also about understanding that matter could be divided into smaller parts. Watch the video “The Millikan Experiment” to see the glow emitted by a cathode ray tube, Thomson’s apparatus, and hear about his groundbreaking work, which effectively demonstrated that the atom was made of divisible parts.
 Self-Check
Self-Check
SC 5. Explain how Thomson calculated the unique charge-to-mass ratio for an electron by completing the following statements and equations.
Step 1: Determine the velocity of the electrons by measuring the_______________ and _______________ fields and using this equation:
_________________
Step 2: Turn off the _____________ field, leaving only the __________ field, which acts perpendicularly to the velocity of the charged particle. In this orientation the magnetic force causes the charged particle to exhibit ________ motion, giving the following expression for the charge-to-mass ratio:
_________________
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 2.
Step 1: Determine the velocity of the electrons by measuring the electric and magnetic fields and using this equation:
![]()
Step 2: Turn off the electric field, leaving only the magnetic field, which acts perpendicularly to the velocity of the charged particle. In this orientation the magnetic force causes the charged particle to exhibit uniform circular motion, giving the following expression for the charge-to-mass ratio:
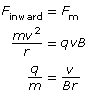
1.6. Page 4
Module 7—Investigating the Nature of the Atom
 Reflect and Connect
Reflect and Connect
One of the most practical uses for Thomson’s ideas is the mass spectrometer like the one used on the Huygens space probe.
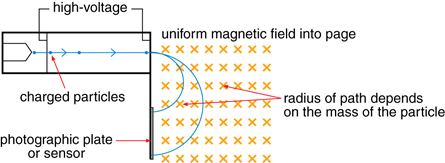
A very large voltage accelerates charged particles. The particles are directed into a magnetic field that is perpendicular to their velocity. Accordingly, a magnetic force is exerted perpendicular to the velocity and the particle travels in a circular path until it hits a photographic plate.
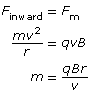
According to the equations that describe a magnetic force that causes circular motion, the radius of the circular path is dependent upon the mass of the particle; therefore, mass can be measured indirectly using the radius of the circular paths.
A mass spectrometer is a powerful application of Thomson’s experiment. In addition to helping humankind explore the chemical composition of other planets and moons, it can be used to identify, by charge and mass, biological chemicals such as toxins, steroids, and drugs. It also has extensive application in pharmaceutical research and quality control in chemical manufacturing.
 Module 7: Lesson 1 Assignment
Module 7: Lesson 1 Assignment
Remember to submit your answers to A 6 and RC 1 to your teacher as part of your Module 7: Lesson 1 Assignment.
A 6. A particle accelerated by a potential difference enters a velocity selector. The particle travels straight when the magnetic field is 0.400 T and the electric field is 6.30 × 105 V/m. Once the electric field is turned off, a sensor determines that the radius, or the particle’s path, is 4.11 cm.
- What is the charge-to-mass ratio of this particle?
- Use the charge-to-mass ratio of the particle to determine whether it is an alpha particle, electron, or proton. Hint: Check your physics data sheet for the charges and masses.
RC 1. Complete questions 1 to 3 of “THEN, NOW, AND FUTURE, The Mass Spectrometer” on page 759 of your physics textbook.
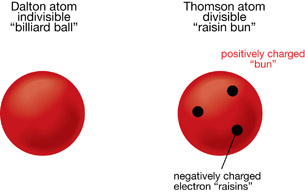
Thomson’s Raisin-bun Model
When Thomson started his charge-to-mass ratio experiments, the current atomic model was Dalton’s indivisible billiard ball model. Dalton determined that each element had a unique atom, and from this he inferred that it was impossible to break matter down further. Thomson’s experiment showed that the electron was much smaller than the smallest atom, a hydrogen atom.
Therefore, Thomson determined that an atom was indeed divisible and must consist of a solid, positively charged mass—the bun—with small, negatively charged electrons embedded in it—the raisins. This explained how a cathode ray tube was able to generate a beam of negatively charged cathode rays—electrons—from any metal. This was the first model of the atom that identified positive and negative charges as divisible parts of the atom.
 Self-Check
Self-Check
SC 6. The Dalton model of the atom, developed from chemistry experiments, indicated that the atom was indivisible. Why was J. J. Thomson able to state confidently that electrons were a component of the atom?
SC 7. Why did J. J. Thomson introduce the positively charged “bun” when he didn’t calculate its charge-to-mass ratio?
 Self-Check Answers
Self-Check Answers
SC 6. J. J. Thomson was able to generate cathode rays (electrons) from cathodes made of different elements. This showed that the cathode rays (electrons) came from within many different elements and must be part of the atom that had previously been undiscovered.
SC 7. J. J. Thomson started with neutral atoms (no net charge), which agreed with Dalton’s model. However, the cathode rays coming from the cathode proved to be negatively charged. In order for the atom to be neutral the remaining part of the atom, once the electrons were removed, must be positively charged. The charges of the positive “bun” and negative “raisins” cancelled each other out and resulted in the neutral atom.
 Module 7: Lesson 1 Assignment
Module 7: Lesson 1 Assignment
Remember to submit your answer to A 7 to your teacher as part of your Module 7: Lesson 1 Assignment.
A 7. How did Thomson’s discovery of the electron change the current Dalton model of the atom and why was this an extremely significant change?
 Module 7: Lesson 1 Assignment
Module 7: Lesson 1 Assignment
Remember to submit the Module 7: Lesson 1 Assignment to your teacher.
1.7. Page 5
Module 7—Investigating the Nature of the Atom
 Lesson Summary
Lesson Summary
In this lesson you focused on the following questions:
- How did the cathode ray contribute to the development of atomic models?
- How did J. J. Thomson determine the charge-to-mass ratio of an electron?
- How did Thomson’s experiment contribute to science and technology?
Early work with vacuum tubes and electric potential led to the discovery of the cathode ray, which served as a vehicle for investigations into the nature of the particles that produced it. Experimentation and observations of cathode rays indicated that they were negatively charged particles capable of being deflected by magnetic and electric fields, and that they possessed the particle characteristics of kinetic energy and momentum.
Using the cathode ray, J. J. Thomson determined the charge-to-mass ratio of the particles by first measuring their speed with perpendicular electric and magnetic fields, and then by using only a magnetic field to produce uniform circular motion. Knowing the strength of the magnetic field, the velocity of the particles and the radius of the circular path they followed in the magnetic field, Thomson concluded that the unique charge-to-mass ratio for all cathode ray particles is 1.76 × 1011 C/kg, a ratio thousands of times larger than that for other common particles, such as the hydrogen ion.
Thomson’s discovery of the electron’s charge-to-mass ratio meant that the atom was indeed divisible into much smaller parts. Using this idea, he proposed the raisin-bun model of the atom in which negative charges are embedded in a blob of positive charge. Although this model is now known to be incorrect, it was the first model that identified positive and negative charges as divisible parts of the atom.
The concepts and theories used in Thomson’s original experiment are now commonly applied in mass spectrometer technology. This technology can be used to identify unknown chemicals by comparing the unique charge-to-mass ratio of the unknown to the charge-to-mass ratio of other known compounds.
Lesson Glossary
cathode ray: a free electron emitted by a negative electrode in a low-pressure environment
1.8. Lesson 2
Module 7—Investigating the Nature of the Atom
Lesson 2—The Millikan Experiment
 Get Focused
Get Focused

This photo, dating back approximately 100 years, shows the lab bench and equipment of physicist Robert Andrews Millikan. Together with his graduate student, Harvey Fletcher, Millikan used the large, black vessel visible on the table to measure a fundamental quantity, one that is related to all the matter in the universe—the elementary charge of an electron!
Inside that vessel, Millikan determined the elementary charge of an electron and, in conjunction with Thomson’s work, he also determined its mass! How was it possible to measure the charge of an electron using a little bit of oil and two electric plates inside a sealed container?
In Lesson 2 you will learn about Millikan’s oil drop experiment and how he determined the elementary charge of an electron.
In this lesson you will answer the following essential questions:
- How were Millikan’s experimental design and apparatus applied to determine the charge of a single electron?
- How did the new fundamental quantity, the elementary charge, inform models of the atom?
- Why did Millikan’s use of scientific judgment cause a controversy among other scientists and scholars?
 Module 7: Lesson 2 Assignment
Module 7: Lesson 2 Assignment
Your teacher-marked Module 7: Lesson 2 Assignment requires you to submit responses to the following:
- Lab—LAB 1
- Assignment—A 1, A 2, A 3, A 4, and A 5
- Discuss—D 1
The other questions in this lesson are not marked by the teacher; however, you should still answer these questions. The Self-Check and Try This questions are placed in this lesson to help you review important information and build key concepts that may be applied in future lessons.
After a discussion with your teacher, you must decide what to do with the questions that are not part of your assignment. For example, you may decide to submit to your teacher the responses to Try This questions that are not marked. You should record the answers to all questions in this lesson and place those answers in your course folder.
1.9. Page 2
Module 7—Investigating the Nature of the Atom
 Explore
Explore
The Millikan Experiment
Shortly after Thomson confirmed the existence of the electron with a charge-to-mass ratio, physicist Robert Millikan designed and performed an experiment to determine the charge on an electron. His well-known oil drop experiment involved spraying tiny oil droplets into a vertical chamber with two metal plates on either end. The oil droplets became charged in the spraying process and when they entered the chamber, they began to fall under the influence of gravity. Millikan could then stop the free-falling droplets and reverse their direction of motion by applying a voltage across the two metal plates. Using a microscope and a timer, he measured the velocity of a single oil droplet in the electric field in order to determine the electrical force acting on it. This allowed him to determine the charge on the oil droplet, since ![]() .
.
It is important to recognize that the charge on the oil droplet was likely due to the presence of many, many extra electrons. Therefore, the charge of an oil droplet will be an integer multiple of the charge on a single electron. Do not confuse the charge of the oil droplet with the elementary charge of a single electron.
How could Millikan determine the charge of a single electron using the charge on multiple oil droplets? By measuring the charge of many droplets and comparing them, he reasoned that the smallest difference in charge among all the droplets would be due to the presence of one extra electron. That small difference in charge would then be equal to the charge of a single electron or the elementary charge. Using the charge on numerous oil droplets and through careful analysis, Millikan discovered that the charges of the oil droplets were always integer multiples of 1.602 × 10–19 C.
elementary unit of charge: the charge of an electron or a proton, 1.60 × 10–19 C
 Watch and Listen
Watch and Listen
Watch the video “The Millikan Experiment: Part 2” to see Millikan's experimental design and apparatus.
How did Millikan’s Apparatus Work?
Open the “Millikan Experiment Simulation” to explore the experimental design.
The apparatus consists of a chamber (as shown below). Looking through the eyepiece, you would see something similar to that shown in the “Reticle View” mode. To switch to the reticle view, click the view button (

Open “Determining the Elementary Charge: Millikan's Oil Drop Experiment” to see how Millikan's oil drop experiment is used to determine the elementary charge.
 Module 7: Lesson 2 Assignment
Module 7: Lesson 2 Assignment
Remember to submit your answers to LAB 1 to your teacher as part of your Module 7: Lesson 2 Assignment.
LAB 1. Use the following procedures to re-enact Millikan’s experiment.
- On the simulation, select the reticle view (
 ) and make sure that the electric field is off (
) and make sure that the electric field is off ( ).
).
- Inject oil droplets into the apparatus by clicking the inject button (
 ) a few times. You should see the droplets moving down.
) a few times. You should see the droplets moving down.
- Toggle the field on and off a couple of times (
 or shortcut key V). When the field is on, you should see some of the droplets move up.
or shortcut key V). When the field is on, you should see some of the droplets move up.
- Look for a droplet that moves both up and down slowly. Select this droplet by clicking on it with your mouse, and verify that it changes colour.
- When your selected droplet is well above the top line of the reticle, turn the field off. As the droplet is falling,
- start the timer (
 or shortcut key M) when it passes the top line of the reticle
or shortcut key M) when it passes the top line of the reticle
- stop the timer (
 or shortcut key M) when it passes the bottom line of the reticle (this is the fall time)
or shortcut key M) when it passes the bottom line of the reticle (this is the fall time)
- start the timer (
- After the droplet has passed the bottom line of the reticle, switch the field on. As the droplet is rising,
- start the timer (
 or shortcut key M) when it passes the bottom line of the reticle
or shortcut key M) when it passes the bottom line of the reticle
- stop the timer (
 or shortcut key M) when it passes the top line of the reticle (this is the rise time)
or shortcut key M) when it passes the top line of the reticle (this is the rise time)
- start the timer (
- Repeat steps 5 and 6 five times for your selected droplet.
- Click the data button (
 ) and view the “Collected Data.” Millikan used the rise and fall times, the mass of the droplet (determined by volume and density), and forces related to air resistance to determine its charge. Note that you will see information related to these values when you click
) and view the “Collected Data.” Millikan used the rise and fall times, the mass of the droplet (determined by volume and density), and forces related to air resistance to determine its charge. Note that you will see information related to these values when you click  and select the “Data Analysis” tab.
and select the “Data Analysis” tab.
LAB 1. Record the average rise velocity: _______________________ average fall velocity: _______________________ charge of your oil droplet: _______________________
Although time-consuming, Millikan’s experiment was instrumental in establishing not only the value of the elementary charge, but also the quantized nature of electric charge. This follows Planck’s earlier discovery that energy is also quantized.
Building on Thomson’s work with the charge-to-mass ratio of an electron, it was then possible to determine the mass of an electron as 9.11 × 10–31 kg.
From J. J. Thomson:
![]()
From R. A. Millikan:
![]()
Combined:
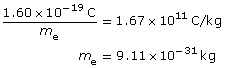
Due to rounding and significant digits, the value is extremely close to the accepted mass of the electron 9.11×10–31 kg.
By accelerating hydrogen ions (protons) through a potential difference and determining their charge-to-mass ratio, it was found that their mass was 1.67 × 10–27 kg. Together, Thomson and Millikan had essentially weighed and measured the charge of some of the smallest fundamental particles that make up matter. They also confirmed the idea that the atom was not the smallest form of matter and that it had divisible parts.
Analysis of Millikan’s Experiment
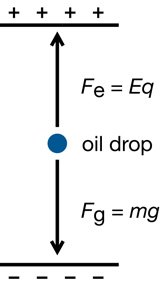
Millikan’s original analysis can be simplified by assuming that the droplets can become suspended between the plates (eliminating any drag forces). That meant that the droplets experienced an electric force upward, exactly equal to the gravitational force pulling them down.
If a droplet were suspended, then the electrical force pulling it up would exactly balance the gravitational force pulling it down. Therefore,
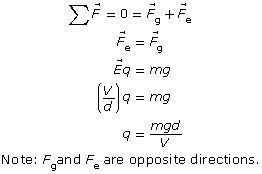
 Read
Read
Read “Millikan’s Oil-drop Experiment” on pages 761 to 764 of the textbook.
Example Problem 1. An oil droplet with a mass of 9.80 × 10–16 kg is suspended between two horizontal charged plates. If the electric field strength between the plates is 2.0 × 104 V/m, what is the charge on the oil droplets?
Given
![]()
Required
the charge on the oil drop
Analysis and Solution
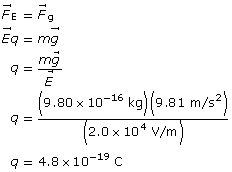
Paraphrase
The charge on the drop is 4.8×10–19 C.
Example Problem 2. An oil droplet with a weight of 4.80 × 10–14 N is suspended between two horizontal charged plates that are 5.00 cm apart. If the potential difference between the plates is 3.0 × 103 V, how many excess electrons does the oil droplet carry?
Given
![]()
![]()
![]()
Required
the number of excess electrons the oil drop carries
Analysis and Solution
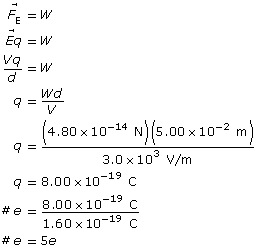
Paraphrase
The oil drop has five excess electrons.
 Self-Check
Self-Check
SC 1. An oil droplet weighs 3.84 × 10–15 N. If it is at rest between two horizontal plates with an electric field strength of 1.20 × 104 N/C, what is the charge on the oil droplet?
SC 2. An oil droplet with a mass of 4.80 × 10–16 kg is suspended between two horizontal charged plates that are 6.00 cm apart. If the potential difference between the plates is 588 V, how many excess electrons are on the droplet?
SC 3. Is it possible to have a particle with a charge of 2.00 × 10–19 C? Explain why or why not.
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 1.
Given
![]()
Required
the charge on the particle
Analysis and Solution
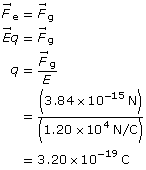
Paraphrase
The charge on the particle is 3.20 × 10–19 C.
SC 2.
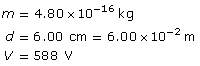
Required
the quantity of excess electrons on the particle
Analysis and Solution
Start with the two equal forces.
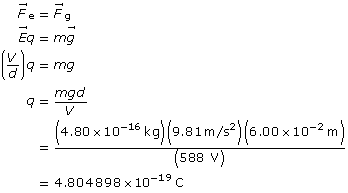
Determine the number of electrons required to obtain the charge.
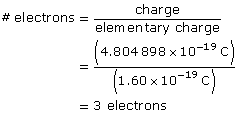
Paraphrase
The particle has three excess electrons.
SC. 3
No, it is not possible to have a charge of 2.00 × 10–19 C because it is not possible to have a quarter of an electron. It is only possible to have whole number multiples of 1.60 × 10–19 C; the charge must be 1.60 × 10–19 or 3.20 × 10–19 or 4.80 × 10–19 C, etc.
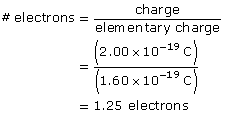
1.10. Page 3
Module 7—Investigating the Nature of the Atom
 Try This
Try This
TR 1. A student does a Millikan oil drop experiment. The device has parallel plates that are 5.00 mm apart. The student determines that the mass of the drop is 2.90×10–15 kg. The student measures how the voltage affects the upward acceleration of the drop. The measurements are listed below.
Voltage (V) |
Acceleration Upward (m/s2) |
0 |
–9.81 |
100 |
–5.40 |
200 |
–0.98 |
300 |
3.43 |
400 |
7.85 |
500 |
12.26 |
- What are the manipulated and the responding variables?
- Draw a graph of the results.
- Use the graph to determine the voltage when the electric force and the force of gravity are balanced.
- Use your value from c. to determine the charge on the drop.
- How many excess electrons are on the drop?
TR 2. An oil droplet with a mass of 7.20 × 10–16 kg is moving upward at a constant speed of 2.00 m/s between two horizontal charged plates. If the electric field strength between the plates is 2.20 × 104 V/m, what is the charge on the oil droplet?
TR 3. An oil droplet with a mass of 3.50 × 10–15 kg accelerates downward at a rate of 2.50 m/s2 when it is between two horizontal charged plates that are 1.00 cm apart. Assuming that the excess charge on the droplet is negative and the top plate is positive, how many excess electrons does the droplet carry if the potential difference between the plates is 533 V?
TR 4. An oil droplet with a mass of 5.70 × 10–16 kg accelerates upward at a rate of 2.90 m/s2 when it is between two horizontal charged plates that are 3.50 cm apart.
- Draw a free-body diagram of the forces acting on the oil drop.
- If the potential difference between the plates is 792 V, what is the charge of the droplet?
 Module 7: Lesson 2 Assignment
Module 7: Lesson 2 Assignment
Remember to submit your answers to A 1, A 2, A 3, A 4, A 5 and D 1 to your teacher as part of your Module 7: Lesson 2 Assignment.
A 1. Why was Millikan unable to use water to make the droplets?
A 2. Why was Millikan’s oil drop experiment so important for the development of models of the atom?
A 3. During a Millikan oil drop experiment, a student records the weight of five different droplets. A record is also made of the electric field intensity needed to hold each droplet stationary between the horizontal charged plates.
Weight (× 10–14 N) |
Electric Field Strength (× 105 N/C) |
1.7 |
1.1 |
5.6 |
3.5 |
6.1 |
3.8 |
2.9 |
1.8 |
4.0 |
2.5 |
Graph the recorded data. Using ONLY the graph, determine the elementary charge.
A 4. In a Millikan-type experiment, two horizontal charged plates are 2.5 cm apart. A latex sphere of 1.3 × 10–15 kg remains stationary between the plates when the potential difference between the plates is 400 V, with the upper plate positively charged.
- What is the type of charge on the sphere?
- What is the electric field intensity between the plates?
- What is the charge on the sphere?
- How many excess elementary charges are on the sphere?
A 5. Two large, horizontal charged plates are separated by 0.050 m. A small plastic sphere is suspended between them and is experiencing a force of 4.5 × 10–15 N.
- If the sphere has four excess electrons, what is the mass of the sphere?
- What is the potential difference between the plates?
 Discuss
Discuss

Copyright © The Nobel Foundation 1923
D 1. Millikan’s experimental discoveries are, to some extent, a product of the scientific culture in which he lived and worked. View the video clip, “Millikan—Scientific Climate” and summarize the scientific climate in which Millikan performed his work.
D 2. Millikan’s published work is very different than that of his scientific journal. This has called into question the scientific process and highlights the use of scientific judgment. View the video clip, “Millikan—Scientific Judgment” and describe how Millikan applied scientific judgment.
 Module 7: Lesson 2 Assignment
Module 7: Lesson 2 Assignment
Remember to submit the Module 7: Lesson 2 Assignment to your teacher.
1.11. Page 4
Module 7—Investigating the Nature of the Atom
 Lesson Summary
Lesson Summary
Millikan’s experimental design was based on measuring the charge of many oil droplets and comparing them, reasoning that the smallest difference in charge among all the droplets would be due to the presence of one extra electron. That small difference in charge would then be equal to the charge of a single electron—the elementary unit of charge. Using the charge on numerous oil droplets and through careful analysis, Millikan discovered that the charges of the oil droplets were always integer multiples of 1.602 × 10–19 C. He reasoned this must be the charge of a single electron, a value that is referred to as the elementary charge.
The charge on each oil drop was determined by measuring, based on the motion of the droplet, the amount of electrical force that acts on it in a uniform electrical field. Oil droplets charged by friction were injected into a sealed vessel with electrodes on either end. Applying a voltage across the electrodes produced an electrical force that acted on the droplet, causing it to move upwards at a constant speed. Measuring the fall and rise speeds, Millikan determined the radius, volume, mass, and, ultimately, the charge of the droplet. By comparing many hundreds of droplets, the smallest integer difference in charge revealed the charge on one electron.
Although time-consuming, his experiment was instrumental in establishing not only the value of the elementary charge, but also the quantized nature of electric charge. It also confirmed the idea that the atom was not the smallest form of matter and that it had divisible parts.
Lesson Glossary
elementary unit of charge: the charge of an electron or a proton, 1.60 × 10–19 C
1.12. Lesson 3
Module 7—Investigating the Nature of the Atom
Lesson 3—The Rutherford and Bohr Models of the Atom
 Get Focused
Get Focused
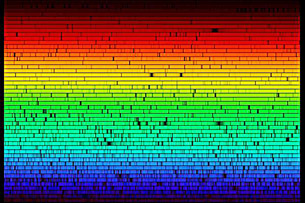
Image courtesy of the National Optical Astronomy Observatory/Association of Universities for Research in Astronomy/National Science Foundation
This image shows the full visible spectrum of colours emitted by the surface of the Sun as observed at the McMath-Pierce Solar Observatory. Recall from Module 5 that when full-spectrum white light passes through a prism, it is dispersed into a spectrum as each wavelength refracts at a slightly different angle. Notice that there are some missing wavelengths, seen as black spots, and that the sunlight is composed mostly of yellow-green wavelengths.
At first glance, the dark spots in this spectrum seem random and unrelated to one another; but they are, in fact, strong evidence that the Sun’s surface is composed of approximately 74% hydrogen and 25% helium. The relative amount and presence of these elements is related to the nuclear reactions that generate the Sun’s energy. In a similar way to that of a mass spectrometer analyzing the composition of Titan’s atmosphere, knowledge of the far and wide originated from an understanding of the close-up and invisibly small. As ideas of the atom evolved from Thomson’s raisin-bun to Rutherford’s planetary system and eventually to Bohr’s concept of the stationary state, the colour of light emitted or absorbed by matter has taken on more significance, hinting at the very composition of the matter with which it interacts!
In Lesson 3 you will explore the fundamental makeup of matter that is revealed by its interaction with electromagnetic radiation and charged particles.
In this lesson you will answer the following essential questions:
- What does the Rutherford Scattering Experiment suggest about the nature of the nucleus, and how did it lead to the planetary model of the atom?
- What is the Bohr model of the atom, and how is the concept of stationary states and energy quantization used to explain how a gas absorbs and emits only certain wavelengths of electromagnetic radiation?
 Module 7: Lesson 3 Assignment
Module 7: Lesson 3 Assignment
Your teacher-marked Module 7: Lesson 3 Assignment requires you to submit responses to the following:
- Lab—LAB 1 and LAB 2
- Assignment—A 1, A 2, A 3, A 4, A 5, A 6, A 7, and A8
The other questions in this lesson are not marked by the teacher; however, you should still answer these questions. The Self-Check and Try This questions are placed in this lesson to help you review important information and build key concepts that may be applied in future lessons.
After a discussion with your teacher, you must decide what to do with the questions that are not part of your assignment. For example, you may decide to submit to your teacher the responses to Try This questions that are not marked. You should record the answers to all questions in this lesson and place those answers in your course folder.
1.13. Page 2
Module 7—Investigating the Nature of the Atom
 Explore
Explore


In their experiment, positively charged helium ions (called alpha particles) from a small sample of radioactive radium were used to bombard gold atoms. When the charged alpha particles encountered gold atoms, they were scattered at various angles. The scattered alpha particles could be observed when they encountered a zinc sulfide screen attached to a microscope.
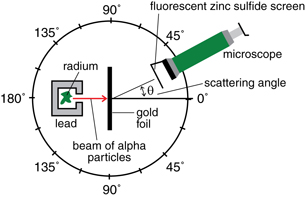
 Read
Read
Read “Rutherford’s Scattering Experiment” on pages 767 and 768 of the textbook.
 Watch and Listen
Watch and Listen

© 2009 University of Colorado. Some rights reserved.
Open the Rutherford Scattering simulation to see how a large nucleus scatters smaller, charged alpha particles. (Note that you will need to save this simulation to your desktop before using it.)
Notice in the simulation that alpha particles are composed of two red protons and two grey neutrons without any electrons, producing the characteristic +2 ion charge. Also notice the small but very distant electron that orbits the large nucleus.
You will see it pass along its circular path in the corners of the viewing area, giving a sense of how small the nucleus and electron are relative to the majority of empty space in the planetary model of the atom.
 Self-Check
Self-Check
SC 1. Adjust the number of protons on the atom using the simulation slider. Set it to 20 protons. Select “Show Traces” to see the path of each alpha particle. Use the term many, few, or rare to complete the following three statements:
- _______ of the alpha particles pass by with little or no scattering, indicating the atom was mostly empty space.
- ______ of the alpha particles are scattered at large angles, indicating the presence of a small, dense nucleus.
- On occasion, _____ alpha particles are scattered straight back toward the source, indicating the presence of a very dense, positively charged nucleus. Presumably, a large electrostatic force of repulsion would be required to reverse the alpha particles’ direction of motion.
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 1.
- Many of the alpha particles pass by with little or no scattering, indicating the atom was mostly empty space.
- Few of the alpha particles are scattered at large angles, indicating the presence of a small, dense nucleus.
- On occasion, rare alpha particles are scattered straight back toward the source, indicating the presence of a very dense, positively charged nucleus. Presumably, a large electrostatic force of repulsion would be required to reverse the alpha particles’ direction of motion.
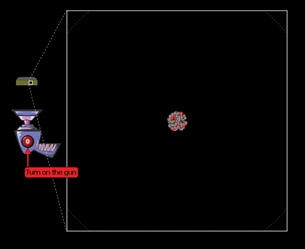
© 2008 University of Colorado. Some rights reserved.
Lab
 Module 7: Lesson 3 Assignment
Module 7: Lesson 3 Assignment
Remember to submit your answers to LAB 1 and LAB 2 to your teacher as part of your Module 7: Lesson 3 Assignment.
Open the Rutherford Scattering simulation once again.
LAB 1. Adjust the number of protons to the maximum of 100. Describe what happens to the amount of scattering that occurs and the angles at which it occurs. How can you explain the relationship between the amount of scattering and the number of protons in the nucleus?
LAB 2. Select the “Plum Pudding Atom” from the upper menu on the simulation. Explain why the alpha particles are no longer scattered.

© 2008 University of Colorado. Some rights reserved.
Failure of the Rutherford Model
According to Rutherford, the scattering alpha particles indicated that within the atom there existed a tiny, but very massive, positively charged core. Rutherford concluded that the atom was not filled with a positively charged substance (as Thomson had described); rather, all the positive charge of the atom was located in a nucleus at the centre of the atom. This nucleus was small but contained almost all the mass of the atom. Thus, Rutherford proposed a nuclear model. In this model the atom has a dense nucleus with relatively vast amounts of empty space through which the electrons can pass. The negative charge of the orbiting electrons was the opposite of the positive charge of the nucleus; so, overall, the atom is still electrically neutral, as Dalton determined.
 Watch and Listen
Watch and Listen
Look at the animated Planetary Model of the Atom again. When you follow this link, do not read the lesson to which the link takes you. Instead, scroll down until you see the animated planetary model of the atom.

There was a problem with the nuclear model of the atom. Recall that positive and negative charges attract. If the nucleus were positively charged, then what stopped the electrons from being sucked into the nucleus? To deal with this problem, Rutherford suggested that the electrons orbit the nucleus, much like the moon orbits Earth or like Earth orbits the sun. The force of attraction between the electrons and the nucleus provides the force necessary to keep the electrons in orbit. Hence, Rutherford proposed a planetary model of the atom.
However, the planetary model was also severely flawed. See if you can figure out what the flaw is by answering the following questions.
 Try This
Try This
TR 1. According Maxwell’s theory of electromagnetism, from Module 5: Lesson 1, what happens when an electron is accelerated? What is given off?
TR 2. In Rutherford’s planetary model of the atom, are the electrons accelerated? If so, what force causes the acceleration?
TR 3. What would happen to an atom if electrons emitted radiation as they orbit the nucleus? Would atoms even exist if they constantly lost energy in the form of emitted radiation?
You should have discovered that, according to Rutherford’s model, atoms are not stable and will collapse in on themselves. According to Maxwell’s electromagnetic theory, when charged particles like electrons are accelerated, they emit electromagnetic radiation. Electrons orbiting a nucleus undergo inward acceleration; thus, they should continuously emit electromagnetic radiation. And if the electrons emit electromagnetic radiation, they should be losing energy. And if the electrons lose energy, they will eventually spiral into the nucleus. What was going on? By the end of the 19th century an adequate model of the atom had not yet surfaced.
 Read
Read
Read “The Bohr Model of the Atom” on pages 771 of your physics textbook.
The Role of Atomic Spectra
In developing a model of the atom, scientists also had to contend with atomic spectra. By the early 1800s, scientists knew that every element emits unique line spectra. For example, when an evacuated bulb is filled with neon gas and a voltage is applied to the electrodes, a characteristic red glow is emitted.
Separating this light by wavelength reveals that neon gas is actually emitting a small collection of unique wavelengths that fall in the red to yellow region of the visible light spectrum. You can see these unique wavelengths identified on the line spectrum below the bulbs. If the bulb were filled with a different gas, for example argon, a blue colour would be produced, with a different and unique line spectrum. The line spectrum is like a chemical fingerprint with each element having its own distinct pattern.
Why did each element have unique spectra, and why was it a line spectra? Somehow, these phenomena must be tied into the mystery of atomic structure.
It is important to understand what a line spectrum means. There are three types of spectra: continuous, bright line (emission), and dark line (absorption). A glowing solid or liquid or high-pressure gas will produce a continuous spectrum but only low-pressure gases will produce line spectra.
Continuous Spectra
All wavelengths (and frequencies) of light are present. In the visible range (400 nm to 700 nm), all the colours are visible.

Bright Line Spectra
An excited low-pressure gas produces a bright line spectrum. The spectrum only consists of lines of particular wavelength. A bright line spectrum is also called an emission spectrum because the gas emits certain wavelengths (frequencies).

Here is a diagram of the experimental set-up to produce a bright line spectrum.
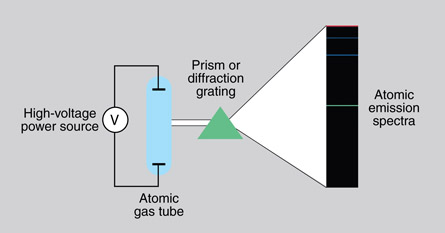
Dark Line Spectra
A dark line spectrum is created when light from a glowing solid or liquid is passed through an unexcited (cool) gas. The typically continuous spectrum (from the glowing solid or liquid) is now missing certain wavelengths—these missing wavelengths appear as dark lines. A dark line spectrum is called an absorption spectrum because the gas absorbs certain wavelengths (frequencies).

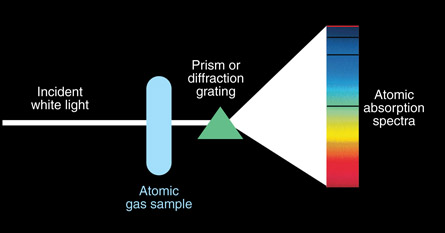
 Self-Check
Self-Check
SC 2. The emission and absorption spectra of hydrogen are displayed above. Compare the position of these lines. What do you notice? Does this mean that a gas can only absorb and emit a limited number of unique EMR wavelengths?
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 2. Both the emission and absorption spectral lines occur in the same place on the spectrum. This means that a gas can only absorb and emit the same, specific wavelengths of EMR.
1.14. Page 3
Module 7—Investigating the Nature of the Atom
 Try This
Try This
It is interesting to re-evaluate Rutherford’s planetary model of the atom in light of atomic spectra. Remember that Rutherford’s model violated Maxwell’s laws of electromagnetism. Ignore that flaw for the moment and evaluate Rutherford’s model by investigating what it predicts about atomic spectra.
 Module 7: Lesson 3 Assignment
Module 7: Lesson 3 Assignment
Remember to submit your answers to A 1 to your teacher as part of your Module 7: Lesson 3 Assignment.
A 1. According to Maxwell’s laws of electromagnetism, the orbital frequency (the number of complete orbits per second) of an electron will match the frequency of the emitted radiation.
- If an electron were to spiral into the nucleus, what would happen to the electron’s orbital frequency?
- If an electron were to spiral into the nucleus, what would happen to the frequency of the emitted radiation?
- If an electron were to spiral into the nucleus, what kind of spectrum would be produced—a continuous or line spectrum? Explain.
- Look at the emission spectrum of hydrogen. What kind of spectrum is this? Does Rutherford’s model predict the correct spectrum?
 Read
Read
Read “Spectroscopy”on pages 771 to 773 of your physics textbook.
spectroscopy: the study of the light emitted and absorbed by different materials
The Bohr Model of the Hydrogen Atom
At the beginning of the 20th century a model was proposed that finally began to answer some of the questions of atomic structure and spectra. In 1913 Niels Bohr proposed a model of atomic structure using hydrogen as the example model. Bohr’s model not only described the structure of the atom, but it also explained atomic spectra and, furthermore, correctly predicted the existence of more atomic lines. Bohr’s model seemed to be everything that physicists were looking for. But there was one problem—Bohr’s model stepped outside the realm of classical physics and ventured into the newly emerging world of quantum physics. This left many scientists skeptical of the model. Nonetheless, Bohr’s model was far superior to any previous model and was accepted as a semi-classical model of the atom.
Bohr’s Postulates
Bohr started with a planetary model of the atom. However, to sidestep the problems that confounded Rutherford, Bohr made several assumptions, including the following:
- Electrons orbit the nucleus. They are held in orbit by an electrostatic force.
-
Electrons can only be in certain, permitted orbits and an electron does not emit radiation when it is in one of these orbits. In these allowed orbits, the energy of the electron is
constant. These orbits are called stationary states, since the electron’s energy is constant. In other words, the energy of the electron is quantized—it can only have certain values (recall the concept of the “particle-in-a-box” from Module 6: Lesson 3 or page 734 in your textbook). Therefore, the allowed orbits can be referred to as energy states.
stationary state: a stable state with a fixed energy level
energy level: a discrete and quantized amount of energy
- An electron only emits radiation when it “falls” from a higher energy state to a lower state. The change in energy of the electron (from the higher state to the lower state) is equal to the energy of the emitted photon, thereby obeying the conservation of energy principle. Similarly, an electron only absorbs radiation when it "jumps" to a higher energy level. Again, the change in energy of the electron is now equal to the energy of the absorbed photon.
- The radii of the allowed orbits are also quantized since each energy state has a specific radius.
Bohr’s model was allowed to have stationary states because of de Broglie’s work on the wavelength of matter. The electron must have a certain speed in order for the Finward and Felectric to be equal. In order for this to occur, the electron has a specific wavelength, which happens to be equal to the circumference of the stationary state. The circumference of the second stationary state is equal to twice the electron’s wavelength and so on. This agrees with quantum theory. See “Figure 15.24” on page 782 of the textbook.
By applying his assumptions, Bohr was able to develop expressions for the allowed energy levels and the allowed radii for the hydrogen atom. Using these expressions, Bohr calculated all the allowed electron energy levels for hydrogen.
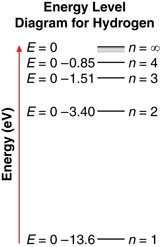
An energy level diagram, like the one shown here, often illustrates energy levels. An energy level diagram displays several things, such as:
- The energy levels of hydrogen are not evenly spaced. As an electron moves to higher and higher levels, the difference in energy between the levels becomes smaller and smaller.
- The energy of each level is reported as a negative number. As an electron moves to a higher energy level, its energy increases (becomes less negative).
- When an electron makes a transition, it moves from one energy level to another. The spacing between energy levels represents the magnitude of the change in energy of the electron. For example, an electron moving from n = 3 to n = 1 has a greater change in energy than an electron moving from n = 3 to n = 2
 Watch and Listen
Watch and Listen
View “Energy Levels of Hydrogen.”
Bohr’s model of the hydrogen atom successfully explained emission and absorption spectra. Not only did Bohr’s model provide a conceptual description of emission and absorption spectra, it also correctly predicted the wavelength of the spectral lines in hydrogen’s emission and absorption spectra. Furthermore, Bohr’s model explained why absorption lines match emission lines.
According to Bohr’s model, an electron only emits or absorbs energy when it moves between energy levels. The energy that is emitted or absorbed by an atom is in the form of a photon.
The amount of energy that is emitted or absorbed is the energy difference between the energy levels. |
The frequency or wavelength of a photon is related to its energy. |
||||||||||||||||||||||||||||||
Expressed as an equation:
|
Expressed as an equation:
|
Example Problem 1. A photon is absorbed by a hydrogen atom, causing an electron to jump from the n = 1 energy level to the n = 3 energy level. Using Hydrogen’s energy level diagram, determine the change in energy of the electron and the wavelength of the absorbed photon.
Given
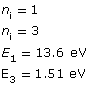
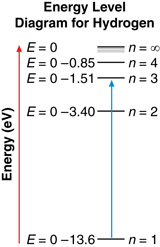
Required
the energy of the released photon and the wavelength of the photon
Analysis and Solution
The red arrow shows that an electron has made a transition from the n = 1 to the n = 3 energy level. The change in the electron’s energy that occurs as a result of the transition is as follows:
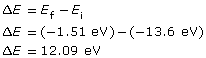
The change in the electron’s energy is equal to the photon’s energy, which is related to its wavelength as follows:
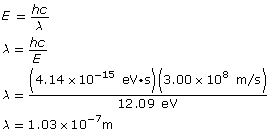
Paraphrase
The energy of the photon is 12.09 eV and it has a wavelength of 1.03×10–7 m.
Watch and Listen
To simulate the example problem transition and see the dark line spectrum that results, open the “Hydrogen Atom Simulation.” On the simulation, press “play” and select the ( ) probability cloud representation. Next, select the n = 3 transition.
) probability cloud representation. Next, select the n = 3 transition.
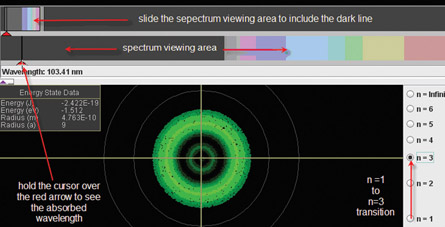
Using this simulation, see if you can verify each of the points below, summarizing the Bohr Model of the atom.
Summary of the Bohr Model
- Absorption (nf > ni). When an electron “jumps” to a higher energy level, it must absorb energy. Each transition requires a specific amount of energy. The dark lines in an absorption spectrum correspond to specific photon wavelengths that are needed for an electron to jump from lower to higher energy levels.
- Emission (nf < ni). When an electron “falls” to a lower energy level, energy is emitted. Each transition emits a specific amount of energy. The lines that are seen in an emission spectrum correspond to specific photon wavelengths that are emitted when an electron jumps from higher to lower energy levels.
- Absorption and emission lines match. For example, the magnitude of the change in energy (ΔE) when an electron rises from n = 1 to n = 2 is equal to the magnitude of the change in energy (ΔE) when an electron falls from n = 2 to n = 1.
-
The absolute value, or the magnitude of the change in energy, is calculated based on the initial and final energy of the electron that undergoes a transition:
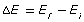
-
The frequency or wavelength of an absorbed or emitted photon can be calculated with
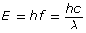 .
.
absorption spectrum: a pattern of dark lines produced when light passes through a gas at low pressure.
emission spectrum: a pattern of bright lines produced by a hot gas at low pressure
 Read
Read
Read “The Bohr Model of the Atom” on pages 773 to 780 of your physics textbook.
 Self-Check
Self-Check
Test your understanding of Bohr’s model of the hydrogen atom by answering the following questions. For questions involving calculations, you may use the Hydrogen Atom Simulation to verify your answers.
SC 3. Look at the assumptions Bohr made. Which of these assumptions "fit" with classical physics and which support the ideas of quantum physics?
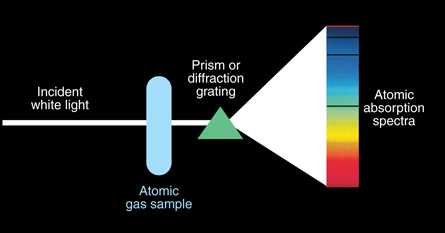
SC 4. Sample equipment to show atomic absorption lines is shown in the diagram below. Absorption lines occur in atomic spectra when an electron absorbs the energy. The electron quickly drops back to the ground state, releasing a photon with the same amount of energy that was absorbed. If the photon is released, why does it not show up on the atomic spectra?
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 3.
| Postulates That “Fit” Classical Physics | Postulates That “Fit” Quantum Physics |
|
|
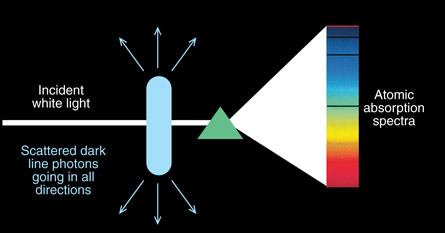
SC 4. The initial incident photons are all projected in one direction through the atomic gas and onto the detector or screen. The photon absorbed by the electron and later released is scattered in a random direction, as shown in the diagram below. As a result, the dark lines are a very few photons re-emitted in that direction but the majority of the photons are emitted in different directions.
Continue to test your understanding of Bohr’s model of the hydrogen atom by answering the following questions. As in the Self-Check activity above, for questions involving calculations, you may use the Hydrogen Atom Simulation to verify your answers.
 Module 7: Lesson 3 Assignment
Module 7: Lesson 3 Assignment
Remember to submit your answers to A 2, A 3, A 4, A 5, A 6, A 7, and A 8 to your teacher as part of your Module 7: Lesson 3 Assignment.
A 2. According to Bohr, why did an atom not collapse in on itself while its electrons travelled around the nucleus?
A 3. Using Bohr’s model, explain what happens in the atom when a photon of light is
- emitted
- absorbed
A 4. Earlier, when you read about the energy levels of hydrogen, you were introduced to an energy level diagram. On this diagram, the n = ∞ energy level is represented. On the applet, complete an n = 1 to n = ∞ transition and observe the energy state data.
- According to the applet, what is the energy of the n = ∞ energy level?
- If an electron is initially in the ground state, how much energy must the atom absorb for this transition to occur?
- What is the radius of the n = ∞ energy level?
- What happens to the atom if the electron “jumps” to the n = ∞ energy level? Hint: Look at the radius of this energy level. Is the electron really part of the atom anymore?
A 5. In the hydrogen atom, the electron jumps from the n = 1 level to the n = 4 level.
- During this transition, is a photon emitted or absorbed?
- What is the change in energy of the electron and what is the wavelength of the emitted or absorbed photon?
- Identify the transition by drawing an arrow on the energy level diagram below, and calculate the wavelength of the absorbed photon.

A 6. An electron in the third stationary state around a hydrogen atom has energy of –1.512 eV. What will the electron’s energy be if the hydrogen atom absorbs a photon with a wavelength of 109 nm?
A 7. What is the shortest wavelength photon that is emitted in the hydrogen atom? What transition emits this photon? Hint: If the wavelength is small, then the energy is large. Looking at the energy level diagram will also help you.
A 8. Bohr’s model of the atom explains why emission and absorption lines match up. Prove this for the hydrogen atom. Choose any transition (and its opposite) and calculate the wavelength of the emitted and absorbed photon. Verify your answer using the applet.
 Try This
Try This
TR 4. Use this Bohr Model of Hydrogen Simulation to shoot a stream of photons through a container of hydrogen gas. Observe how photons of certain energies are absorbed, causing changes in the orbits of electrons. Build the spectrum of hydrogen based on photons that are absorbed and emitted.
TR 5. You can also use this Bohr Model: Introduction Simulation to fire photons and observe how an absorbed photon changes the orbit of an electron, and how a photon is emitted from an excited electron. Calculate the energies of absorbed and emitted photons based on energy level diagrams. The light energy produced by the laser can be modulated, and a lamp can be used to view the entire absorption spectrum at once.
1.15. Page 4
Module 7—Investigating the Nature of the Atom
 Reflect and Connect
Reflect and Connect
The Bohr model of the atom, in conjunction with spectroscopy, can be used to identify unknown gases based on either their absorption or emission line spectrums. The missing parts of the sun’s spectrum can be explained using the absorption spectrum of hydrogen and helium, indicating their presence on the surface of the sun.
Using a similar technique, it is possible to identify the chemical composition of other stars and galaxies by examining the wavelengths of light that come from them.
RC 1. Open the Star Spectra Simulation and see if you can identify the presence of known elements using the line spectrum from astronomical objects such as stars and galaxies.
 Going Beyond—The Quantum Mechanical Model of the Hydrogen Atom
Going Beyond—The Quantum Mechanical Model of the Hydrogen Atom
With the development of quantum mechanics throughout the 20th century, a quantum mechanical model of the atom has been devised. Bohr’s model of the hydrogen atom was a semi-classical model—it took ideas from classical physics and extended them to quantum physics. A quantum mechanical model of the hydrogen atom does not rely on classical physics; rather, it is built upon ideas of wave functions and probabilities.
In the quantum model of the atom, electrons do not exist in specific orbits around a nucleus. Rather, the quantum model computes probabilities for the location of an electron around a nucleus. Remember that Bohr’s model stated that an electron can only exist in specific orbits, with a specific energy and radius. The quantum model denies these absolute ideas. An electron can exist anywhere around a nucleus—the probability distribution represents the most likely location of the electron.
The Hydrogen Atom Simulation can be used to compare the quantum model of the hydrogen atom to Bohr’s model of the hydrogen atom. On the simulation, the allowed Bohr radii are drawn as circles. Remember that the scintillations (flashes of light) represent probabilities—the brighter the flash, the greater the probability.
 Self-Check
Self-Check
SC 5. Play the Hydrogen Atom Simulation and select the probability cloud mode (![]() ). Make sure that the electron is in its ground state (n = 1). Vary the scintillation rate using the slider.
). Make sure that the electron is in its ground state (n = 1). Vary the scintillation rate using the slider.
- The diagram below shows the first three allowed Bohr radii for hydrogen. On a diagram like the one shown, sketch the probability density for an electron in the ground state (n = 1), according to the quantum mechanical model of hydrogen. Indicate the region(s) of highest probability on your diagram.
- How does the quantum mechanical model for the ground state of hydrogen compare to the Bohr model for the ground state?
SC 6. Reset the simulation so that the electron is in the ground state (n = 1). Do a transition to the second energy level. Again, vary the scintillation rate and toggle between modes.
- Sketch the probability density for an electron in the second energy level. Indicate the region(s) of highest probability on your diagram.

- How does the quantum mechanical model for an electron in the second energy level of hydrogen compare to the Bohr model for the ground state?
 Self-Check Answers
Self-Check Answers
Contact your teacher if your answers vary significantly from the answers provided here.
SC 4.
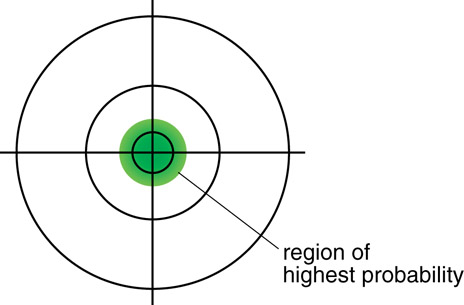
- The quantum mechanical model is illustrated using a wide probability density cloud, but at a distance farther from the nucleus than the thin circular line of the Bohr model for the ground state.
SC 6.
- The quantum mechanical model is illustrated using a wide probability density cloud, whereas the Bohr model is illustrated by thin, circular lines.
 Module 7: Lesson 3 Assignment
Module 7: Lesson 3 Assignment
Remember to submit the Module 7: Lesson 3 Assignment to your teacher.
1.16. Page 5
Module 7—Investigating the Nature of the Atom
 Lesson Summary
Lesson Summary
In this lesson you explored the following questions:
- What does the Rutherford Scattering Experiment suggest about the nature of the nucleus, and how did it lead to the planetary model of the atom?
- What is the Bohr model of the atom, and how is the concept of stationary states and energy quantization used to explain how a gas absorbs and emits only certain wavelengths of electromagnetic radiation?
Rutherford’s Scattering Experiment was significant because he expected to verify the J. J. Thomson model of the atom and have the alpha particles travel straight through the gold foil. Instead, he was surprised to discover that some of the alpha particles were significantly deflected by something in the atom. His observations led him to develop a new model of the atom with a small, dense centre with most of the mass and a positive charge that was named the nucleus. In order to balance the charge, the electrons orbited around the nucleus like planets orbiting around the sun. He maintained the net neutral electrical charge and the electrons as discovered by Thomson, but the discovery of the nucleus was a new advance.
Bohr quickly realized that the Rutherford model with the orbiting electrons was flawed. In order for electrons to orbit (move in a circle), they must constantly accelerate. According the Maxwell’s electromagnetic theory, this means that the electrons would constantly be emitting EMR and losing energy. As a result, the electrons would slow down and spiral into the nucleus. Clearly, this wasn’t happening, so changes to the model were needed. Bohr used spectroscopy to examine the patterns of specific wavelengths of EMR absorbed and emitted by gaseous elements. From these observations he determined that the electrons were in specific orbitals and could only gain and release specific amounts of energy—quantized energy. Bohr established that electrons in the atom have quantized orbitals and that the electrons absorb specific energy photons to go up orbital levels and release specific energy photons when they drop down orbital levels. However, Bohr could not explain why there were orbital levels at those specific energies. Bohr’s model is considered semi-classical because it incorporates the quantum but does not include the wave-duality of the electron, which was discovered later.
The quantum mechanical model links the Bohr model with de Broglie wavelengths for electrons. The stationary orbitals are stable because the circumference of the orbital is a whole number multiple of the wavelength of the electron. If the orbital circumference is not a whole number multiple, then the electron destructively interferes with itself and the orbital is not stable. Due to Heisenberg’s uncertainty principle, it is impossible to predict exactly where the electrons are located, but the probability cloud of where the electron is can be calculated. Quantum theory cannot predict exactly where the electron is, but it allows physicist to calculate the probability of it being in a specific location. Future physics courses will show you that physics has changed from classical physics with exact answers to quantum physics with probabilities of answers.
Theories about the composition and structure of the atom are constantly changing, and it is important to remember that scientific models are human inventions. They are tools developed to help explain physical phenomena. As such, models are not a literal representation of the world. Rather, they illustrate a way of looking at the world and a way of understanding certain phenomena. As science continues to uncover secrets of the atom, new models will evolve.
Lesson Glossary
absorption spectrum: a pattern of dark lines produced when light passes through a gas at low pressure
emission spectrum: a pattern of bright lines produced by a hot gas at low pressure
energy level: a discrete and quantized amount of energy
spectroscopy: the study of the light emitted and absorbed by different materials
stationary state: a stable state with a fixed energy level
1.17. Module Summary/Assessment
Module 7—Investigating the Nature of the Atom
 Module Summary
Module Summary
Module 7 focused on how the quantization of energy in atoms and nuclei reveal the electrical nature of the atom. Early work with vacuum tubes and electric potential led to the discovery of the cathode ray, which served as a vehicle for investigations into the nature of the particles that produced it. Experimentation and observations of cathode rays indicated that they were negatively charged particles capable of being deflected by magnetic and electric fields and possessing the particle characteristics of kinetic energy and momentum.
Using the cathode ray, J. J. Thomson determined the charge-to-mass ratio of these particles by first measuring their speed with perpendicular electric and magnetic fields and then by using only a magnetic field to produce uniform circular motion. Thomson concluded that the unique charge-to-mass ratio for all cathode ray particles is 1.76 × 1011 C/kg, a ratio thousands of times larger than that of any other common particle, such as the hydrogen ion. The large ratio could indicate a relatively large charge and/or relatively small mass. In this case it was the small mass that led to a large q/m (charge-to-mass) ratio.
The concepts and theories used in Thomson’s original experiment are now commonly applied in mass spectrometer technology. This technology can be used to identify unknown chemicals by comparing the unique charge-to-mass ratio of the unknown compound to that of the charge-to-mass ratio of other known compounds.
Millikan discovered the elementary charge of an electron in his now-famous oil drop experiment. By finding the smallest difference in charge between thousands of oil drops, he was able to conclude that the electron has a charge of –1.602 × 10–19 C—a value that is now referred to as the elementary charge. Although time-consuming, his experiment was instrumental in establishing not only the value of the elementary charge, but also the quantized nature of electric charge—an oil drop’s charge can only be an integer multiple of the elementary charge. It also confirmed the idea that the atom was not the smallest form of matter and that it is divisible into subatomic particles.
After the electron had been identified and studied, the nature of the nucleus was revealed by Rutherford’s scattering experiment, leading to the planetary model of the atom. This model was difficult in terms of classical physics and required significant revisions, which were done courtesy of Niels Bohr. Bohr’s Semi-Classical Model described electrons orbiting the nucleus in certain stable states (energy levels) with specific energies and radii. This quantization of the energy explained patterns in the EMR spectrum of certain elements, leading to the identification of atoms and elements on distant objects such as the sun.
Finally, the quantum mechanical model of the atom described the electron position using a probability distribution, a distribution that indicates where the electron is most likely to be found.
Theories about the composition and structure of the atom are constantly changing, and it is important to remember that scientific models are human inventions. They are tools developed to help explain physical phenomena. As such, models are not a literal representation of the world. Rather, they illustrate a way of looking at the world and a way of understanding certain phenomena. As science continues to uncover secrets of the atom, new models will evolve. Hence, an artistic representation of electrons orbiting a nucleus is just that—a representation of something that cannot be seen by the human eye but can be understood by the human brain.
Module Assessment
Use the information below to answer the following questions.
Question 1
In a modified Millikan apparatus, a small charged object with a mass of 4.7 × 10–15 kg is suspended by the electric field that is between charged parallel plates. The table below shows how the balancing voltage depends on the distance between the plates.
Plate Separation (mm) |
Balancing Voltage (x 103 V) |
10.2 |
0.992 |
21.0 |
1.99 |
25.1 |
2.44 |
29.0 |
2.85 |
35.0 |
3.52 |
55.0 |
|
- Graph the balancing voltage as a function of the plate separation with the manipulated variable on the horizontal axis.
- Calculate the slope of the graph and describe the physical quantity or quantities that this slope represents.
- Using the slope, or another suitable averaging technique, determine the magnitude of the charge on the suspended mass.
- Determine the balancing voltage required when the plates are separated by 55.0 mm.
Clearly communicate your understanding of the physics principles that you are using to solve this question. You may communicate this understanding mathematically, graphically, and/or with written statements.
Question 2
Describe the development of the quantum mechanical model of the atom. In your explanation, start with the Dalton model of the atom and finish with the quantum mechanical model of the atom. For each of the five models include
- a description of the significant experiments
- the reason the observations of the experiment showed a new model was needed
- a description of how scientists changed each model into the next model
1.18. Module Glossary
Module 7—Investigating the Nature of the Atom
Module Glossary
absorption spectrum: a pattern of dark lines produced when light passes through a gas at low pressure
cathode ray: a free electron emitted by a negative electrode in a low-pressure environment
elementary unit of charge: the charge of an electron or a proton, 1.60 × 10–19 C
emission spectrum: a pattern of bright lines produced by a hot gas at low pressure
energy level: a discrete and quantized amount of energy
spectroscopy: the study of the light emitted and absorbed by different materials
stationary state: a stable state with a fixed energy level