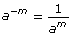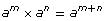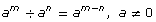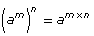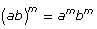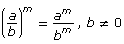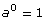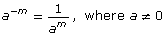Lesson 5: Integral Exponents
| Site: | MoodleHUB.ca 🍁 |
| Course: | Mathematics 10C |
| Book: | Lesson 5: Integral Exponents |
| Printed by: | Guest user |
| Date: | Friday, 19 December 2025, 3:54 AM |
Module 2: Roots and Powers
Lesson 5: Integral Exponents
Focus

© SFC/shutterstock
This lesson discusses exponents and how they are combined. You will find many applications of exponents in the real world. Exponents describe how populations grow, how automobiles depreciate in value over time, how investments compound, and how radioactive material decays, to name a few.
In this lesson you will review the exponent laws you learned in your previous math studies. The exponent laws are a great example of patterns. You will learn that the observation of patterns can lead to the discovery of other exponent laws. You will also use known exponent laws to come up with two new ones: the zero exponent law and the integral exponent law. In your project for this lesson you will examine the use of binary codes in the way computers operate. You will practise encrypting and decrypting using this code.
Outcomes
At the end of this lesson, you will be able to
- explain, using patterns, why
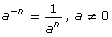
- apply the exponent laws to expressions with rational and variable bases and integral exponents, and explain the reasoning:
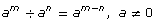
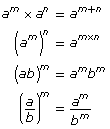
Lesson Questions
- How are the properties of exponents used to evaluate and simplify algebraic expressions?
- How can patterns be used to uncover mathematical truths?
 Lesson Completion and Assessment
Lesson Completion and Assessment
As you work through each lesson, complete all the questions and learning activities in your binder using paper and pencil, clearly labeling your work (they refer to this as your course folder). These include the Are you Ready, Try This, Share and Self Check questions. Check your work if answers are provided. Remember that these questions provide you with the practice and feedback that you need to successfully complete this course.
Once you have completed all of the learning activities, take the Lesson Quiz. This is the assessment for each lesson and is located under the Assess tab or by using the Quizzes link under the Activities block.
** Note – Share questions may have to be done on your own depending on your learning situation**
Module 2: Roots and Powers
Launch
This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully.
Are You Ready?
Complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.
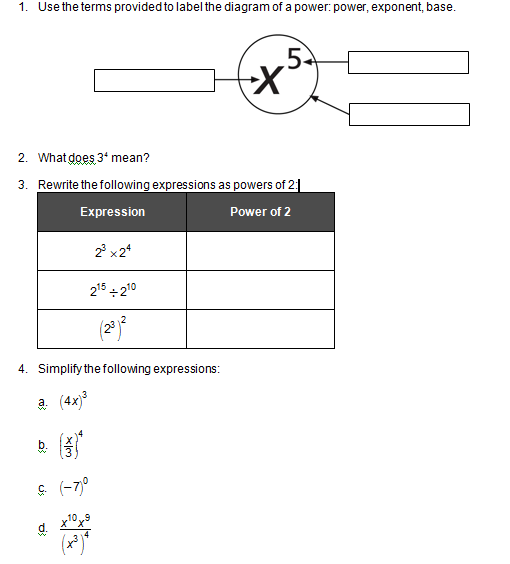
Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
 Refresher
Refresher
Use the “Exponent” applet to review the definition of exponent. Follow the links from there to explore the definitions of power and base. Click on “power” to use the demonstration applet to apply the definitions.
Try “Exploring Laws of Exponents” to review the exponent laws. There are seven laws altogether. The first six were covered in your previous math studies. The seventh one, the negative exponent law, will be introduced in this lesson.
You will want to select the “Explore It” tab at first. You can either explore the applet on your own or if you prefer to have some structure to your exploration, choose the “Print Activities” option to use with the applet.
Materials

© Michael C. Gray/shutterstock
You will need the following materials to complete Math Lab: Examining Patterns.
- eight pieces of shoelace licorice of equal length (alternative to licorice – eight French fries)
- knife
Module 2: Roots and Powers
Discover
In this lesson you will be working with the exponent laws you learned in your previous math courses. You will also be introduced to two other exponent laws.
The Math Lab will prepare you for the mathematical concepts you will learn later in the lesson.
 Math Lab: Examining Patterns
Math Lab: Examining Patterns
Go to Math Lab: Examining Patterns, print it (or copy by hand) and complete it.
Once you have completed these questions, use the link below to check your answers. Make any corrections or notes as needed. File this in your binder( course folder).
Module 2: Roots and Powers
Explore

© Gina Smith/shutterstock
Exponents can be used to describe very large numbers and very small numbers. For example, the number of strands of hair on a person’s head is about 1.0 × 105, while the diameter of a single strand of hair can be as small as 2.0 × 10−5 m. If you laid each strand of hair side by side, what would be the distance from one end to the other? In this lesson you will review the exponent laws and learn other ones that will help you solve questions like this.
Glossary Terms
Add the following terms to your "Glossary terms":
- base
- exponent
- power
- reciprocal
----------------------------------------------------------------
In your previous math courses, you studied the exponent laws. The following chart summarizes those exponent laws. The chart also provides examples for you to see why each law works. Read over this chart carefully. There is chart to print, later in this section.
|
Exponent Law |
General Case |
Example |
|
Product Law |
|
|
|
Quotient Law |
|
|
|
Power of a Power |
|
|
|
Power of a Product |
|
|
|
Power of a Quotient |
|
|
Zero Exponents
It is easy to think of the expression 23 as three factors of 2 multiplied together. In other words,
23 = 2 × 2 × 2
While this is true for all values of the exponent that is a natural number, in the case of 20, it is not appropriate to think of the power as zero factors of 2 multiplied together. In fact, if you thought of it this way, you might think the answer is zero. After all, the absence of any factors should leave you with nothing! However, if you look at your chart from the licorice investigation in the Discover section, you will see that this is not true.
In that investigation you used patterns to complete the table. Starting with 8, each number in the first row is half of the previous number. That is because you were always removing (or eating) half of the amount of licorice that was left. In the second row, you expressed each number in the first row as a power of 2, starting with 23, then 22, then 21, and so on with the exponent diminishing by one each time.
According to the pattern, what was the value equal to 20?
You can verify this result algebraically using the laws of exponents.
You know the quotient law states that ![]()
Then it follows that
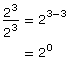
![]()
This rule applies to bases other than 2. Suppose the base is assigned the variable a:
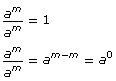
Therefore, 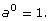 This is the zero exponent law. This law can be added to the chart above.
This is the zero exponent law. This law can be added to the chart above.
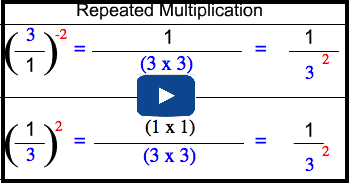
Negative Exponents
Just as it is difficult to think about zero factors of 2 multiplied together in the case of the expression 20, it is perhaps even more difficult to think about negative three factors of 2 multiplied together. That just doesn’t make sense!
Refer again to your chart from the licorice investigation. Consider the expanded form of each power of 2:
23 = 2 × 2 × 2
22 = 2 × 2
21 = 2
Do you see that each time you decrease the exponent by 1, you are dividing by a factor of 2? What will happen if you continue this progression?
|
|
|
|
|
A negative exponent means to divide by that number of factors instead of multiplying! So 5−3 is the same as ![]() This pattern reveals the general rule that
This pattern reveals the general rule that ![]() where
where ![]() (You can also rearrange the equation to get
(You can also rearrange the equation to get ![]() where
where 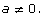 )
)
This is called the integral exponent law. This law can be added to the chart above.
Exponents Law Chart
Please print and store in your course folder ( binder) for future reference.
Module 2: Roots and Powers
 Watch and Listen
Watch and Listen
Use the “Negative Exponents” interactive to reinforce the discussion about negative exponents.
There are other ways of understanding negative exponents. The following chart presents two ways of verifying the result in the example using the laws of exponents.
|
Using the Quotient Law |
Using the Zero Exponent Law |
|
|
Two numbers are reciprocals of each other if their product is equal to 1. (for example, since
Therefore, |
The following examples show a practical way of thinking of negative exponents.
Example 1
Evaluate 2−3.
Solution
Look at
23 = 8
The reciprocal of 8 is 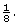
Therefore, 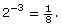
Example 2
Evaluate 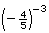
Solution
Look at
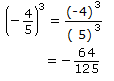
The reciprocal of 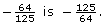
Therefore, 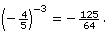
Example 3
Simplify 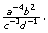
Solution
You can think of the expression as
![]()
![]()
 Tips
Tips
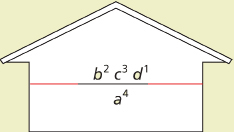
A fun way to think about negative exponents that can help you to simplify expressions easily is to view each power in the numerator and denominator as tenants in a house managed by you, the landlord.
In the case of the last example, there are four tenants: a−4 and b2 living upstairs, and c−3 and d−1 living downstairs.
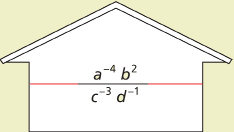
You can think of the sign of the exponents as a measure of how happy each tenant is with the surroundings. A positive exponent, as in the case of b2, means the tenant wants to stay put. A negative exponent, as in the case of a−4, c−3, and d−1, means the tenant is unhappy and looking to move to another floor.
As the landlord, you have the power to shuffle the tenants around. If you leave the powers with the positive exponents where they are (because they are happy tenants), and shuffle the powers with the negative exponents to either the denominator or the numerator (because they are unhappy in their present position), then you will get an equivalent expression with only positive exponents.
 Read
Read
Go to the textbook and work through the examples that deal with negative exponents. You will be focusing on questions that involve negative exponents, but you will also have to remember how to apply the other exponent laws you have previously learned. As you work through each step, try to identify the exponent law being applied.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Evaluating Powers with Negative Integer Exponents” on page 231 and “Example 1: Simplifying Numerical Expressions with Rational Number Bases” and “Example 2: Simplifying Algebraic Expressions with Integer Exponents” on pages 238 and 239.
In Example 1.d) on page 239 you will see rational exponents or fractions as exponents. You will learn about rational exponents in the next lesson, but you can still apply the exponent laws you have learned thus far to solve this question. Give it a shot!
 Self-Check
Self-Check
Apply what you have learned to the following questions from your textbook. Remember that when you approach the task of simplifying exponents, there is often more than one way to do so. The solutions to the Self-Check questions show one method, but if you get the same result using a different method, then you may also be right. In those cases, check with your teacher to see if your method is mathematically sound.
Foundations and Pre-calculus Mathematics 10 (Pearson)
SC 1. Complete “Check Your Understanding” question 1 on page 231.
SC 2. Complete “Check Your Understanding” question 1 on page 238.
SC 3. Complete “Check Your Understanding” question 2 on page 239.
 Try This 1
Try This 1
Use the laws of exponents to solve the problems.
Complete the following questions in your course folder (binder).
Remember to show your work by indicating which laws you apply at each step. Also be sure to express your answers using positive exponents.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 1. Complete the following:
a. “Exercises” questions 5, 8, 15 and 20 on pages 233 and 234
b. “Exercises” questions 4.b, 4.d, 7.b, 7.c, 8, 9, and 11.b. d on pages 241 to 243
Once you have completed these questions, use the link provided below to check your work.
Module 2: Roots and Powers
 Lesson Assessment
Lesson Assessment
Complete the lesson quiz posted under the Assess tab or by using the Quizzes link under the Activities block. Also, ensure your work in your binder (course folder) is complete.
 Project Connection **NOT ASSIGNED**
Project Connection **NOT ASSIGNED**

© Andrea Danti/shutterstock
There are reasons for the use of encryption other than security. In some cases, a code is developed in order to relay messages in a more practical manner. Morse code, for example, is a code that makes use of rhythms to transmit information. Letters and numbers in Morse code are based on particular sequences of dots and dashes. As a result, you would only need two input signals to communicate with Morse code, not 36 keys—the minimum you would need on a keyboard to communicate all the alphanumeric characters.
In this section you will look at a coding system similar to Morse code but that is used by computers. The information inside a computer is coded using binary numbers. All the data a computer stores and uses to run applications is based on the binary number system that only uses the digits 0 and 1. Just as the decimal number system you use every day is based on powers of 10, the binary number system is based on powers of 2.
Here is how you can count to 10 in binary:
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
You can get an idea for how binary works by comparing it to the decimal system:
In the decimal system the position of each digit corresponds to a power of 10. For example,
|
102 |
101 |
100 |
Expansion |
Number in Base 10 |
|
2 |
9 |
(2 × 101) + (9 × 100) |
29 |
|
|
1 |
1 |
4 |
(1 × 102) + (1 × 101) + (4 × 100) |
114 |
In the binary system the position of each digit corresponds to a power of 2. For example,
|
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
Expansion |
Number in Base 2 |
Number in Base 10 |
|
1 |
1 |
1 |
0 |
1 |
(1 × 24) + (1 × 23) + (1 × 22) + (1 × 20) |
11101 |
29 |
|||
|
1 |
1 |
1 |
0 |
0 |
1 |
0 |
(1 × 26) + (1 × 25) + (1 × 24) + (1 × 21) |
1110010 |
114 |
At this time, go to the Unit 2 Project and complete the Module 2: Lesson 5 portion of the project.
 Going Beyond
Going Beyond
In the Discover section of this lesson you repeatedly cut a stick of licorice in half. Theoretically, you can never eat the entire licorice because there would always be a small piece left. Yet it seems like you should be able to eat all the licorice at some point. When a group of statements seems to contradict each other or defies intuition, those statements represent a paradox.

The ancient Greek philosopher Zeno of Elea posed a series of problems known as Zeno’s paradoxes. The most famous of these paradoxes involves the Greek hero Achilles and the tortoise. In it, Achilles challenges the tortoise to a footrace. Achilles is so confident of winning that he gives his opponent a 100-m head start. By the time Achilles runs 100 m, the tortoise has moved another 10 m. By the time Achilles makes up the 10-m distance, the tortoise has advanced another 1 m. This scenario repeats itself with the tortoise advancing one-tenth of its previous move each time Achilles reaches its previous marker. If this continues, Achilles will never catch the tortoise. Yet experience shows that in these cases, the faster runner should win. The paradox lies in the seeming contradiction of the last two statements.
Here are some ideas for further research:
- There are paradoxes in many disciplines including logic, physics, languages, and mathematics. See if you can identify other examples of paradoxes.
- If you started with $200, then added $100, then added $50, and so on indefinitely, how much would you have? (The answer is not an infinite amount of money.)
Module 2: Roots and Powers
Lesson 5 Summary
In Lesson 5 you investigated the following questions:
- How are the properties of exponents used to evaluate and simplify algebraic expressions?
- How can patterns be used to uncover mathematical truths?
In this lesson you reviewed and applied exponent laws. By examining patterns and using the laws you learned in previous math courses, you were able to discover the zero exponent law and the integral exponent law. You used the quotient law to show that a0 = 1. Through experimentation with licorice, you learned that each time the exponent of a power is reduced by 1, the value of the power is diminished by a factor equal to the base. You used the results of this experiment to uncover the law that 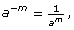 where
where  These laws are summarized in the following chart:
These laws are summarized in the following chart:
|
Exponent Law |
General Case |
|
Product Law |
|
|
Quotient Law |
|
|
Power of a Power |
|
|
Power of a Product |
|
|
Power of a Quotient |
|
|
Zero Exponent Law |
|
|
Integral Exponent Law |
|
The practice of examining patterns is fundamental to the development of theorems and laws in mathematics. Those laws or rules can then be combined with other patterns to uncover further laws. Thus mathematical truths are revealed.
You learned the exponent information that is summarized in the chart. It is extremely important to understand how the laws work as opposed to just memorizing the shortcuts. There is a lot of information here, and if you find you are forgetting some of the laws, then likely you need to spend more time writing the steps out so you can see what is happening and understand how the laws work.
In the next lesson you will learn about the rational exponent law. You will investigate a pattern that shows how radicals are related to powers and exponents! You will also practise your troubleshooting skills by examining solutions to problems that contain errors.


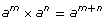
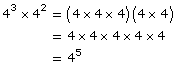
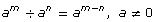
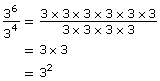
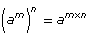
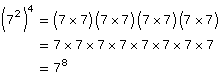
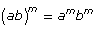
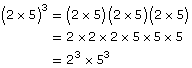
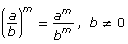
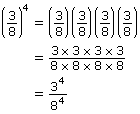
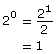
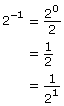
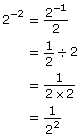
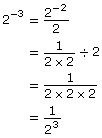
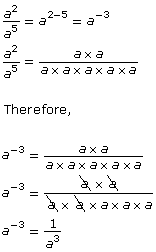
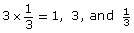 are reciprocals of each other)
are reciprocals of each other)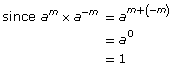
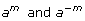 are reciprocals of each other
are reciprocals of each other