Lesson 1: Multiplying Binomials: Launch

Math 10C Module 3 Lesson 1

Module 3: Polynomials

Launch

Are You Ready?

Complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.

1. Determine each product without using your calculator. Show each step.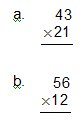

2. Add or subtract the following terms.
a. 2x +5 + 3x - 1
b. 3x² -x + 6x - 4
c. 4x + 6x² - 3 - 8x + 2x -4x² + 6 + 2x² - 2
3. Determine each product.
a. (5x)(7x)
b. 3m * 4n
c. (8x³)(2x⁵)
4. What is the distributive property?
5. Use the distributive property to expand each expression.
a. x(x + 6)
b. -7 (x + 2)

Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.

Answers

If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.

Refresher

The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources either before or after you try the Are You Ready? questions. Your teacher may also direct you to this section to review specific concepts.

-------------------------------------------------------------

Go to “Multiplication of Whole Numbers” to watch a demonstration on how to multiply two-digit numbers by
two-digit numbers. Under “Topics,” choose the eighth item titled “Multiplication with Symbols (2-Digit by 2-Digit)–Demo.”

----------------------------------------------------------------

The lesson titled “Multiplying Monomials” is a review of how to multiply monomials. You may want to obtain a set of algebra tiles from your teacher, use the “Algebra Tiles Template,” or use the interactive “Arranging Algebra Tiles” to follow along as you proceed through the examples.

------------------------------------------------------------------

Then go to “Adding and Subtracting Polynomials.” As you review the lesson, you will see a reference to the zero principle. The zero principle states that if you have the same number of positive and negative elements in a set, then the sum of those elements is zero. In terms of algebra tiles, the zero principle allows for an equal number of positive tiles and negative tiles to be cancelled since their sum is zero.

----------------------------------------------------------------

Go to “Distributive Property” at the Mathematics Glossary website to find out how the distributive property can be applied to the multiplication of monomials with polynomials.

---------------------------------------------------------------

Materials IMPORTANT

You will want to have a set of algebra tiles handy as you proceed through this lesson. You can do one of the following:

Obtain a set of algebra tiles from your teacher.
Print two copies of the Algebra Tiles Template. You can either print each one on different coloured paper, or you can colour each of them by hand using two different colours. You need two different colours to help you to differentiate between positive and negative algebra tiles.
Use the interactive “Arranging Algebra Tiles.” This applet will provide an unlimited supply of each type of tile. As necessary, you can use a screen capture tool to paste each arrangement into your glossary, notes, or assignment.