Lesson 1: Multiplying Binomials
Module 3: Polynomials
Explore
Glossary Terms

© iofoto/shutterstock
In this lesson you will learn how to multiply binomials. Add these terms and their definitions to your "Glossary Terms".
- algebra
- algebra tiles
- binomial
- distributive property
- monomial
- numerical coefficient
- polynomial
- variable
Once you have added these definitions to your handout, return the Glossary Terms document to your course folder.
You will explore two methods of multiplying binomials. These are the area method and the distributive property method.
Earlier in this lesson, you may have used algebra tiles. Using algebra tiles is a great way to start exploring the concept of multiplying binomials. These tiles can be moved around into different configurations and can, therefore, help you visualize the products of polynomials.
Area Method
Multiplying two binomials is very much like finding the area of a rectangle. In this case, each binomial forms a dimension of the rectangle.
In this section you will arrange algebra tiles into rectangular areas. Before you get started, you need to know a rule about the arrangement of algebra tiles.
A tile is correctly placed when its side lengths match the side lengths of adjacent pieces.
The following illustration shows how algebra tiles can be placed in relation to each other. Examples are shown of both proper placement and improper placement of tiles. Notice that in the proper placement of algebra tiles, the dimension of any given tile is located next to the same dimension of another tile.

The following illustrations show two ways in which algebra tiles are improperly placed. In the first case, the tiles in the bottom row are not aligned with those in the top row. In the second case, the top edge of any of the first four smaller squares in the bottom row does not share the same dimension with the larger square above it.

 Watch and Listen
Watch and Listen
Use the applet “Algebra Tiles Activity” to practise placing algebra tiles properly.
Now that you have an understanding of how algebra tiles can be placed, you can use them in a multiplication array to multiply binomials.
Retrieve your results from the Discover section. In TT 3, you should have completed the following multiplication array:
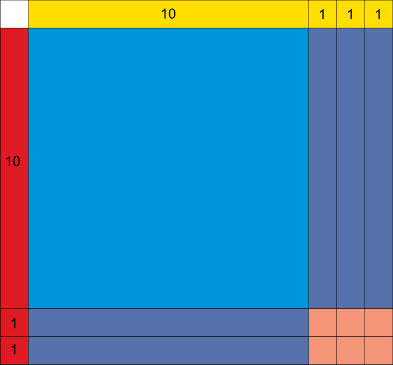
The sum of the top row is 13, and the sum of the left column is 12. This array helps you to find the product of 13 × 12.
The main body of the array is made up of a large square (blue) measuring 10 × 10, five rectangles (purple) measuring 10 × 1, and six smaller squares (salmon) with dimensions 1 × 1.
The total area is the following:
![]()
You may wish to confirm your answer using a calculator. Was the product of 13 × 12 also 156? Using algebra tiles or an array helps visualize multiplication using the area model. You can also see that, in multiplication, it is possible to break numbers into their factors and then determine the products of those smaller numbers. The final product is the sum of the smaller products.
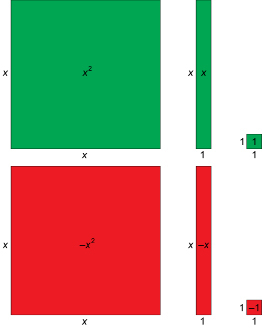
Multiplying binomials is based on the same idea.
 Watch and Listen
Watch and Listen
Watch the video titled “Algebra Tiles: Multiplying Positives” to see how you can multiply binomials with algebra tiles and a multiplication array. This method is also known as the area method or rectangle method.
This method works equally well when there are negative terms in the binomial.
Next, watch the next two videos to see how you can find the product of binomials with negative terms:
- “Algebra Tiles: Multiplying Negatives”
- “Algebra Tiles: Multiplying Binomials with Mixed Signs”
As you watch, try to discover the two instances when positive tiles can be used.
----------------------------------------------
----------------------------------------------
The Arranging Algebra Tiles applet is a helpful tool for using the area method. As you complete the following Self-Check questions, you may do the work using the applet and then paste the screen captures into your answers.
----------------------------------------------
 Self-Check
Self-Check
Use the area method to find the following products.
SC 1. (x + 4)(x – 2)
SC 2. (x – 3)(x – 1)
SC 3. (2x – 1)(x + 3)
Distributive Property Method
The distributive property can be summarized in this way:
![]()
In other words, the product of a monomial and a polynomial is equal to the sum of the products of the monomial multiplied by each term of the polynomial.
The distributive property can be used to multiply binomials.
You can also multiply binomials by thinking of it in the same way that you think about multiplying two-digit numbers together.
For example, to represent the multiplication of 34 × 27, you can set up a multiplication array by breaking each number into tens and ones.
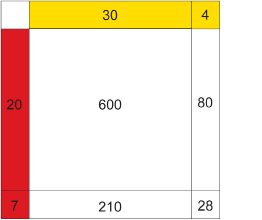
Notice that each number in the top row is multiplied by each number in the left column.
The product is the sum of the products in the array.
600 + 210 + 80 + 28 = 918
Now think about it without using the array.

Whether you use an array or the distributive property to model the multiplication, the process is the same: multiply each digit of the first number by each digit of the second number.
Multiplying binomials is based on the same idea. For example, to represent the multiplication of (x + 3)(x + 2), you can set up a multiplication array by breaking each binomial into an x-term and a constant.
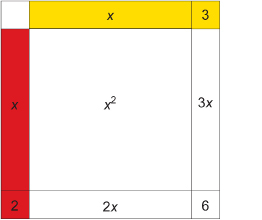
Just as you noticed in the previous array, each term in the top row of this array is multiplied by each term in the left column.
The product of the binomials is the sum of the products in the array.
x2 + 2x + 3x + 6
In the next example, you will perform the same calculation but without the array.
Example
Multiply (x + 3) by (x + 2) using the distributive property.
Solution
(x + 3)(x + 2)
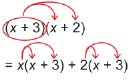
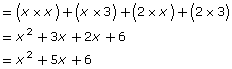
It is a good idea to use arrows in your solution (as shown in the solution) to help you keep track of which terms you are multiplying together. Remember that you need to multiply each term of one binomial with each term of the other binomial.
 Tip
Tip
A way that you can remember how to multiply binomials using the distributive property is to use the acronym FOIL. The table summarizes the meaning of each letter.
|
Letter |
Meaning of |
What the Letter Means |
|
F |
First |
Multiply the first terms of each binomial. |
|
O |
Outer |
Multiply first term of the first binomial and the last term of the second binomial. |
|
I |
Inner |
Multiply the second term of the first binomial and the first term of the second binomial. |
|
L |
Last |
Multiply the last terms of each binomial. |
A visual representation of FOIL is as follows.
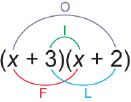
To watch a video to see to use the acronym FOIL to multiply binomials together, go to the Internet and type the keywords “Math Dude” into a search engine. These keywords should take you to the Montgomery County Public Schools website. On the right side of the website, look for the heading “Algebra 1 Unit 6.” Then choose the video titled “Multiplying Polynomials.”
 Watch and Listen
Watch and Listen
You can practise multiplying binomials. Use "The FOIL Method- Practice"

AND
Watch this Khan academy video for more reinforcement on "How to multiply Binomials".
 Read
Read
Work through the example of multiplying binomials in the textbook that you are using for this course. Take the time to examine the two methods of determining the product.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Read “Example 1: Multiplying Two Binomials” on page 161. What are the similarities between the method of multiplication using algebra tiles and that of using the distributive property?
 Self-Check
Self-Check
Complete the following questions.
SC 4. (5x – 4)(x + 2)
SC 5. (x2 + 3)(x2 + 3)
SC 6. (x – y)(3x – 2y)
SC 7. (y + 4)2
SC 8. (a + b)(c + d)
 Try This 9
Try This 9
Once you are comfortable with the Self-Check solutions, practise doing more questions relating to the concepts in this lesson.
Complete the following in your course folder ( binder).
TT 9. Foundations and Pre-calculus Mathematics 10 (Pearson), questions 5, 9, and 12 on pages 166 and 167.
Use the link below to check your answers to Try This 9.
Possible TT9 (Try This 9) Solutions





