Lesson 2
1. Lesson 2
1.7. Explore 3
Module 2: Radical Functions
In Try This 1 and Try This 2 you discovered some of the patterns between the domain and range of y = f(x) and 
The domains of the square root functions are restricted in the areas of the original graph where y < 0. That is, any portion of the original graph that lies below the x-axis will not appear in the graph of the square root function. The range is restricted because the square roots of negative values are not real numbers. As a result, the range contains only values that are greater than or equal to zero.
You will now examine methods to graphically or algebraically compare the domains and ranges of a function and its square root.
Read “Example 2” on pages 82 and 83 of the textbook. Note the following:
- Method 1 uses technology to graph and then compare domains and ranges.
- Method 2 uses algebra to identify the x-intercepts, y-intercept, and the maximum or minimum value of the original function. You then determine the corresponding key points on the graph of
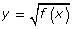by taking the square root of the original function’s maximum or minimum value. If there are x-intercepts, these intercepts stay the same. The domain and range can then be determined by using the key points.
Self-Check 2
Complete questions 5.b. and 5.c. and questions 6.b. and 6.c. from “Practise” on page 87 of the textbook. Answer
You have graphed f(x) and 
when the equations are given to you. What happens if you are only given a graph of y = f(x)? Could you graph 
from a graph of y = f(x)?
Review “Example 3” on page 84 of the textbook.
Self-Check 3
- Complete “Your Turn” on page 85. Answer
- Complete questions 8.a. and 8.c. and question 11 on page 87. Answer
