Lesson 2

To this point in the lesson you have only been dealing with coterminal angles—angles where the terminal arms coincide. In Try This 3 you will explore angles formed by incomplete revolutions. You will explore how the distance a horse moves in a circle relates to the radian measure of the angle the horse travels.

Try This 3

In Try This 2 you looked at a horse walker with a radius of 6 m. The horses took 12 s to walk 1 revolution. You found the distance of 1 revolution to be

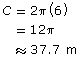
1. What distance, and through what central angle, will the white horse travel after each specified amount of time that is less than 12 s? Complete a table similar to the one shown. The first column has been completed for you.
   
   

   	6 s	3 s	4 s
   Fraction of 1 Revolution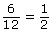	of a revolution
   Distance Travelled by White Horse to the Nearest Tenth of a Metre, or Arc Length	circumference × amount of a revolution
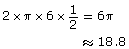   Diagram of Rotational Angle in Standard Position
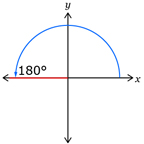   Angle of Rotation in Degrees	360° × 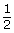= 180°
   Angle of Rotation in Radians	2π × 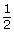= π

2. Explain how you determined the distance travelled by the horse.

3. Explain how you determined the angle of rotation.

 Save your responses in your course folder.

Share 2

Discuss your responses to Try This 3 and the following questions with a classmate.

1. How do your strategies compare for finding the distance travelled and the angle of rotation? What are the similarities and differences between your strategies and your partner’s strategies?
2. What is the relationship between the distance around a circle (arc length) and the radian measure of the angle?

 If required, save a record of your discussion in your course folder.