1. Lesson 4

1.10. Explore 6

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

In Try This 3 you determined the exact value for You may have used the unit circle, reference triangles, or some other process to determine the value of the trigonometric ratio. Determining Exact Values for Trigonometric Ratios will demonstrate using the unit circle or reference triangles to determine the exact values for trigonometric ratios.

 

Watch Determining Exact Values for Trigonometric Ratios to see how to determine the exact value of sec

 

 

This is a play button that opens Determining Exact Values for Trigonometric Ratios.

 

Self-Check 4

 

textbook

  1. Complete “Your Turn” at the bottom of page 195 in the textbook. Answers
  2. Complete questions 1.c., 1.e., and 1.g. on page 201 in the textbook. Answers

This is a picture of a student using a calculator.

iStockphoto/Thinkstock

You can calculate approximate values for trigonometric ratios by using your calculator.

tip bar

Your calculator can determine the trigonometric values for angles measured in degrees or radians. You will need to choose the correct mode for your calculator. Check your calculator manual to change from degree to radian mode and back again. For example:

  • To calculate sin 75°, you would use degree mode. So, sin 75° = 0.965 925 826…
  • To calculate 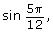you would use radian mode. So, 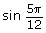= 0.965 925 826…


Most calculators do not have cosecant, secant, or cotangent buttons. You can still calculate the value of these ratios by using your calculator.

 

Example

 

Determine the approximate value of sec (−4.1), and round your answer to four decimal places.

 

Solution

 

For this question, your calculator should be in radian mode since −4.1 is a radian measure. Remember, when there is no degree symbol, assume the angle is measured in radians.

 

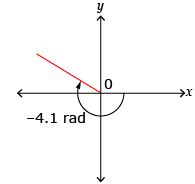
This is a sketch of the terminal arm of – 4.1 radians on an x and y axis.

In which quadrant would the angle −4.1 terminate?

 

The angle terminates in quadrant 2. The value of the cosine ratio is negative in quadrant 2 because the value of the x-coordinate is negative in quadrant 2. If the cosine ratio is negative, the value of the secant ratio will also be negative.

 

 

 

 

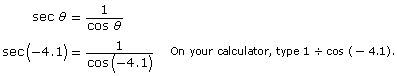
If you did not get this answer, check to see if your calculator is in radian mode.

 

Self-Check 5

 

textbook

  1. Complete questions 2.c., 2.g., and 2.j. on page 201 in the textbook. Answers
  2. Complete question C1 on page 204 in the textbook. Answers

glossary

Add the following terms to your copy of Glossary Terms:

  • cosecant
  • secant
  • cotangent

formula sheet

Add the following formulas to your copy of Formula Sheet: