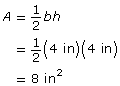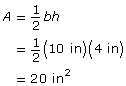Module 4
1. Module 4
1.11. Page 6
Module 4: Area
Bringing Ideas Together
In Explore you discovered that the area of a trapezoid is composed of the areas of two triangles.
For the trapezoid in Explore, with height h and parallel sides a and b,
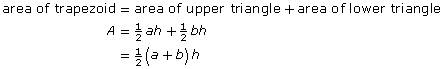
One way of remembering this formula is to think of ![]() as the average of the lengths of the two parallel sides, a and b. So,
as the average of the lengths of the two parallel sides, a and b. So,
area of a trapezoid = average of the two parallel sides × height
The multimedia piece “Area of a Trapezoid” shows another way to explain why the formula ![]() works.
works.
Work through the following examples to test the use of the average length of parallel sides to calculate area.
Example 4
A piece of fabric for a quilt is pictured below.
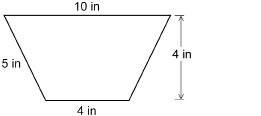
What is the area of this piece of fabric?
Solution
Method 1
Apply the formula ![]() .
.
a = 10 in
b = 4 in
h = 4 in
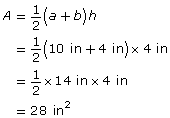
The area of the piece of fabric is 28 in2.
Method 2
Apply the following formula.
area = average of the two parallel sides × height
To find the average of the parallel side, add the sides together and divide by 2.
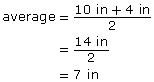
So,
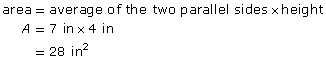
The area of the piece of fabric is 28 in2.
Method 3
Divide the trapezoid into two triangles by dividing from the upper-left vertex to the lower-right vertex. This shows that there are two triangles making up the trapezoid. Each triangle has a height of 4 in.
|
Lower Triangle
b = 4 in, h = 4 in
|
Upper Triangle
b = 10 in, h = 4 in
|
The area of the composite shape is the sum of the areas of these triangles.
![]()
The area of the piece of fabric is 28 in2.
More Composite Figures
Investigate how simple shapes can be combined to form composite figures in “Exploring Composite Figures.” (You may ignore circles for now; circles will be covered in the next lesson.)
In the next few examples you will examine areas of composite figures.
Example 5
As part of a community historical project, Anita is planning to paint a mural on the back of her garage.
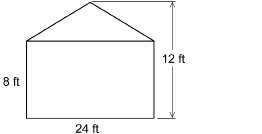
What area can Anita paint?
Solution
Step 1: Separate the composite figure into simpler shapes.
Step 2: Transfer the dimensions of the composite figure to these simpler shapes.
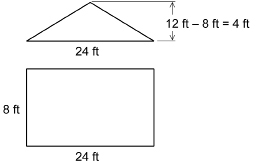
Step 3: Calculate the area of each simple shape.
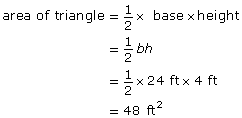
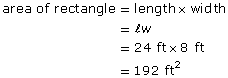
Step 4: Combine the areas of the simpler shapes.

Anita could paint a mural 240 ft2 in area on the back of her garage.
Now it’s your turn!
 Self-Check
Self-Check
SC 7. The following flag is used by maritime ships to signal “starboard.”
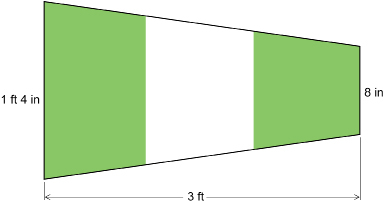
What is the area of this flag?
SC 8. Hong is going to apply some fertilizer to the lawn next to her house. The lawn is shaped like this.
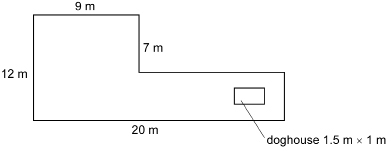
What is the area of the lawn?
SC 9. A stop sign is a regular octagon. Each side is 10 in long. The distance from the top of the sign to the bottom is approximately 24.14 in.
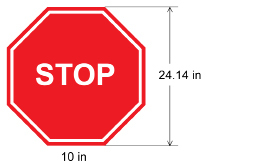
What is the area of the stop sign to the nearest square inch?
SC 10. Look at the composite shape.
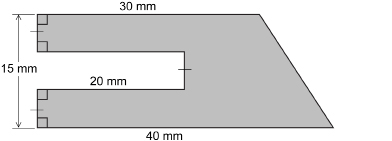
You can infer that the top and bottom of the shape are parallel from the small squares in the left corners of the illustration. There is a rectangular cutout 20 mm deep with a height one-third of the total height of the shape.
Calculate the area of the composite shape.
 Mastering Concepts
Mastering Concepts
Try this question. When you are finished, check your answer.
In Explore, you derived the formula for a trapezoid by dividing the shape into two triangles. You could have found the formula by dividing the trapezoid into a parallelogram and a triangle.
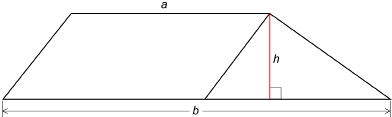
Show that this method also gives you the formula ![]() .
.