1. Lesson 2

1.5. Explore

Mathematics 30-1 Module 1

Module 1: Function Transformations

 

Explore

 

A reflection is a transformation that produces a mirror image of the original figure. The “mirror” line is called the line of reflection. Although any line can be a line of reflection, you will mainly use the x-axis and y-axis in this lesson.

 

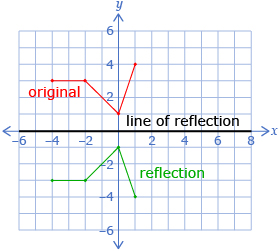
The diagram shows a function on a coordinate grid passing through the points (–4, 3), (–2, 3), (0, 1), and (1, 4). This function is labelled “Original.” A second function labelled “Reflection” passes through the points (–4, –3), (–2, –3), (0, –1), and (1, –4). A line of symmetry is labelled Line of Reflection.

 

In Try This 1 you may have noticed that reflecting a point across an axis just changed the sign of one of the coordinates. Look ahead to see how this pattern can be formalized.

 

Try This 2
  1. Using the information from Try This 1, describe what happens to the coordinates of an individual point as the point is reflected across an axis. Determine a mapping that will represent this.

    Line of Reflection

    Description

    Mapping

    y-axis

     

    (x, y) → (__, __)

    x-axis

     

    (x, y) → (__, __)
  2. An invariant point is a point on the graph that remains unchanged after a transformation has been applied to it. What point(s) would you expect to be invariant when reflecting across the
    1. x-axis?
    2. y-axis?

course folder Save your responses in your course folder.

Think of a value y such that y = −y.