Lesson 3

Explore

Did You Know?

When people hear the word stretch, they often think of something getting larger. In this course, stretching refers to something getting larger or smaller. One reason for using this word is to avoid confusion when using the term compress. Although “compress by a factor of ” seems like it should mean the object will become half its size, it actually means the object will double in size. Think about why this is true.

In Try This 1 you explored what happened to the shape of a graph when you multiplied all of the x-coordinates of a function by a constant or when you multiplied all of the y-coordinates by a constant. The change in shape seen is called a stretch. In this lesson you will focus on stretches about the x-axis or the y-axis. When you're stretching about an axis, it is useful to think of a function in terms of the equation y = af(bx). In Try This 2 you will explore the outcomes of changing a and b for a function of this form.

Try This 2

Open Stretching/Reflecting y = af(bx).

1. Select the square root function button .
   
   

   Notice the point highlighted on the function that follows. This highlighted point shows where a particular point moves as you adjust a and b. The original coordinates and transformed coordinates of this point are listed at the bottom of Stretching/Reflecting y = af(bx). Make sure you pay attention to this information during Try This 2.
   
   

    

   

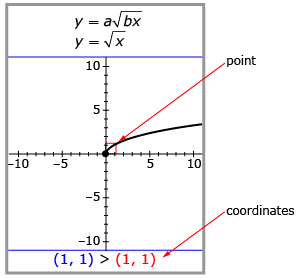
2. Drag the red point along the graph to (4, 2); then use the applet to complete a table like the one that follows.
   
   

   Value of a	Value of b	Coordinates of Original Point	Coordinates of Transformed Point	Description/Diagram of How the Point Changed	Description/Diagram of How the Function Changed
   1	1	(4, 2)	(4, 2)	no change	no change
   3	1
   0.7	1
   −2	1
   1	4
   1	0.5
   1	−2
   Student Choice
   Student Choice

3. For positive a- and b-values, what effect does each of the following have on a function?
   1. increasing a
   2. decreasing a
   3. increasing b
   4. decreasing b
4. Press the “SET FCN” button on the applet and experiment with a different function. Do you still agree with your responses from question 3?

Save your work in your course folder.

Share 2

With a partner or group, discuss the following questions based on the table you created in Try This 2.

1. What effect does a negative a or b have on the function? Where have you seen this effect before?
2.  
   1. What mathematical relationship is there between a and how an individual point on the function y = af(bx) moves?
   2. What mathematical relationship is there between b and how an individual point on the function y = af(bx) moves?
   3. Where would you expect to find an invariant point for each type of stretch?