Module 5
1. Module 5
1.7. Page 2
Module 5: Angles
Get Started
In the next activity you will examine angles found around you and learn to identify congruent angles.
 Try This
Try This
Work with a partner, if possible.
You may recall working with congruent angles in previous math courses. Do you remember what a congruent angle is? Take a look at the image of the star quilt in “What is a Congruent Angle?” Scroll over the image, and you will see a sample of congruent angles highlighted for you in the quilt. Do you remember what congruent means now?
Now, take a few minutes to look around your surroundings. Inside a building or outdoors there are many examples of congruent angles. For instance, look at where the corner of the room meets the ceiling.

At the ceiling corner there are three congruent angles. Why?
congruent angles: angles with the same measure
Nature’s patterns display congruent angles. Look for them on images of a snake’s skin, a butterfly’s wings, and a snowflake. Can you identify the congruent angles in these images?

© SRNR/shutterstock

© Inna Petyakina/shutterstock

© John David Bigl III/shutterstock
TT 1. Make a list of at least ten sets of congruent angles you see around you. Save your list. You will be asked for items from your list in the Lesson 2 Assignment.
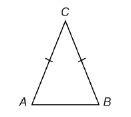
As well as in your home or in nature, you encountered congruent angles in geometric shapes you explored in previous mathematics courses. For example, suppose you were shown an isosceles triangle—a triangle with two equal sides.
You would write ![]() and would shade those angles as follows.
and would shade those angles as follows.
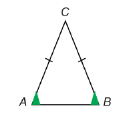
View the applet “Isosceles Triangle,” which demonstrates that the angles across from the equal sides in an isosceles triangle are congruent.
Save your answers for TT 2 through TT 5 in your course folder; you will be asked for your answers in the Lesson Assignment.
For each of the shapes in TT 2 through TT 5, first list and then shade the congruent angles in a sketch of the shape.
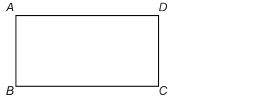
TT 2. ABCD is a rectangle.
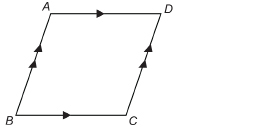
TT 3. ABCD is a parallelogram.
TT 4. ![]() intersects
intersects ![]() , forming angles 1, 2, 3, and 4 as shown.
, forming angles 1, 2, 3, and 4 as shown.
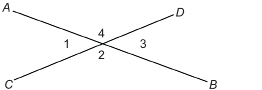
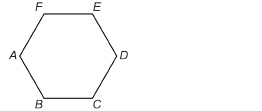
TT 5. ABCDEF is a regular hexagon—a polygon with six equal sides.