1. Module 5

1.18. Page 3

Mathematics 10-3 Module 5 Lesson 4

Module 5: Angles

 

Explore

 

In the Get Started section you reviewed the angle relationships based on the three angles of a triangle. There are also angle pairs that have special relationships. Having words to describe angle pairs will be of help in discovering angle relationships.

 

adjacent angles: angles that share a common vertex and lie on opposite sides of a common arm

The coloured angles are adjacent angles.

 

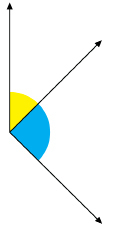
This illustration shows two angles sharing one arm and a common vertex. The angles are coloured yellow and blue.

 

Self-Check

 

SC 3. This illustration shows three pairs of angles.

 

This illustration shows three pairs of angles. The first pair has two rays sharing a common vertex and a third ray with a vertex on one of the first two rays a short distance from the vertex. The second pair has two rays forming one angle, and a short distance away are two more rays forming a second angle. The third pair has one line with two rays extending at right angles from the same point on the line. The angles are on opposite sides of this right angle.

 

Explain why all of these pairs are not adjacent pairs.

 

Compare your answer.

 

Intersecting Lines

 

The sizes of adjacent angles at the intersection of two lines are connected in a special way.

 

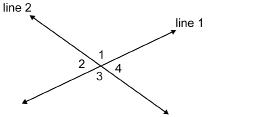
This illustration shows two lines intersecting. The lines are labelled line 1 and line 2. The angles are labelled counterclockwise from the top as 1, 2, 3, and 4.

 

Can you identify pairs of adjacent angles at the intersection of line 1 and line 2?

 

Self-Check

 

SC 4. Using the diagram in Intersecting Lines, complete the following statement. Then justify your answer.

 

 

 

∠1 + ∠2 = ____°.

 

SC 5. What is the sum of the measures of a pair of adjacent angles formed by intersecting lines?

 

Compare your answer.

 

supplementary angles: two angles that add up to 180°

 

In a pair of supplementary angles, one angle is the supplement of the other.

In the diagram you’ve been considering, ∠1 and ∠2, a pair of adjacent angles, are supplementary angles. Not all supplementary angles are adjacent. This is demonstrated in the following question.

 

Self-Check

 

SC 6. In the following angle pairs, ∠c has a measure of 60°, and ∠d has a measure of 120°.

 

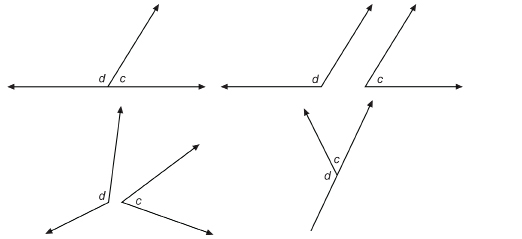
The top left diagram shows angles d and c sharing a common vertex and horizontal baseline. The top right diagram shows angles d and c beside each other with parallel arms but not touching. The bottom left diagram shows angles d and c arranged in different orientations beside each other. The bottom right diagram shows angles d and c sharing a common vertex and diagonal baseline.

 

Which of these angles are supplementary angles but not adjacent angles?

 

Compare your answer.

 

Around the Corner

 

You saw that the angles at the intersection of two lines were connected in a special way. There is also a special connection between the sizes of adjacent angles making up a right angle.

 

Look at ∠a and ∠b in the following diagrams.

 

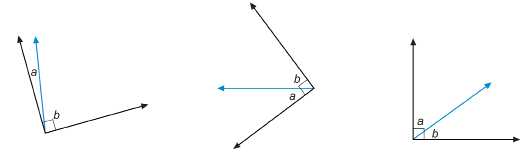
This is a series of three diagrams depicting right angles in various orientations. In each frame, a ray emanates from the vertex of the right angle to produce two adjacent angles within the right angle. The adjacent angles are labelled A and B.

 

SC 7. Complete the following statement. Then justify your answer.

 

∠a + ∠b = ____°.

 

Compare your answer.

 

complementary angles: two angles with measures that add up to 90°

 

One angle is called the complement of the other.

∠a and ∠b are not only adjacent angles; they are also complementary angles. But not all complementary angles are adjacent. This is demonstrated in the following question.

 

Self-Check

 

SC 8. In the following diagram, ∠c has a measure of 60° and ∠d has a measure of 30°.

 

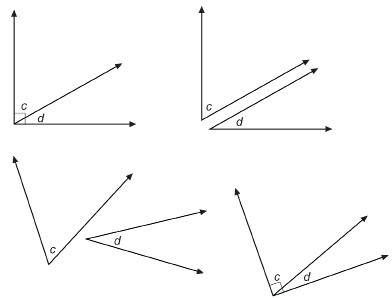
The top left diagram shows a right angle with a horizontal base divided into angles c and d by a common ray. The top right diagram shows angles d and c beside each other with parallel arms but not touching. The bottom left diagram shows angles d and c arranged in different orientations beside each other. The bottom right diagram shows a right angle with an oblique base divided into angles c and d by a common ray.

 

Which of the angles shown are complementary angles but not adjacent angles?

 

Compare your answer.

 

Angle Pairs in Your World

 

Complementary angles often occur at right-angle corners. For example, look at the square corners of a picture frame. The pieces that form the frame are cut at angles that add up to 90°. Commonly, those complementary angles are each 45°, but they don’t have to be equal. One could be 40° and the other could be 50°.

 

A photo shows a wooden picture frame with cuts visible at the square corners.

© YuM/shutterstock

 

There are countless examples of adjacent angles in nature, construction, art, and architecture.

 

What type of angle pairs are found in each of the following pictures?

 

A photo of a spiderweb shows rays overlaid on spokes on the web to highlight supplementary adjacent angles.

© Martin Maun/shutterstock

 

A photo of a framed roof shows rays overlaid on rafters to highlight adjacent angles. © John Leung/shutterstock

A photo shows rays overlaid on parts of the frame of a geodesic structure to highlight a pair of adjacent angles.

© Jim Parkin/4071317/Fotolia


 

Share

 

In Lesson 2 you identified angles in the topic for your Unit 3 Project. Now is a perfect time to find an example of a supplementary or adjacent angle pair. Use a sketch or photo to illustrate one of these angle pairs from your topic. Share these images with others and see what they have done—this might help you with your own project.

 

Save a copy of your work in your course folder as you will need this information for your Unit 3 Project.

The following are pairs of adjacent angles: ∠1 and ∠2, ∠1 and ∠4, ∠4 and ∠3, and ∠3 and ∠2.
The spiderweb shows supplementary adjacent angles, the framed room shows adjacent angles, and the silver exterior shows adjacent angles.